论文 - 《Bi-DeepViT: Binarized Transformer for Efficient Sensor-Based Human Activity Recognition》
关键词 - 高效、二值化、DeepViT、HAR、传感器

1 引言

人体活动识别（HAR）是一种通过传感器采集数据来解读个体或群体行为与动作的技术，正从实验室走向工业界，在医疗服务、新型人机交互方式以及健康管理等方面发挥着重要作用。
深度学习技术 in HAR
- CNN 在大规模图像分类方面表现出色，因此许多 HAR 系统将原始时间序列信号转换为频域图像（即频谱图）进行处理。
- RNN 则擅长建模原始序列信号中的时间依赖关系。许多先进的 RNN 架构，如长短期记忆网络（LSTM）和门控循环单元（GRU），已被应用于人体活动分类任务。
- 结合 CNN 和 RNN 的混合神经网络也被用于融合频域特征和时域特征，从而提升 HAR 的准确率。
Transformer
- 基于 Transformer 的模型在 NLP 和 CV 任务中展现出卓越性能，这也激发了其在 HAR 领域的应用研究兴趣。
- 由于传感器信号的频谱图结构与 RGB 图像相似，ViT 可以被直接用于基于传感器的人体活动识别。
HAR 系统向边缘计算范式发展
- 原因：尽管在 HAR 研究中提高准确性仍然是首要目标，但越来越多的研究开始关注计算效率和推理速度的重要性。位于网络边缘的传感器不断产生数据流，将所有数据上传到云端既不现实，也会导致传输延迟和高带宽成本。
- 挑战：边缘设备通常资源受限且功耗受限，而深度学习模型往往计算密集，并且Transformer 模型相比其他深度学习模型更加耗费资源。
模型压缩技术
- 常见的模型压缩技术有四种：量化、剪枝、低秩分解和知识蒸馏。
- 量化是最常用的技术之一，它通过使用更少的比特位来存储模型权重和激活值来压缩模型。二值化是量化的极端形式，将激活值和权重都用1 bit 表示。这种极大的复杂度降低使二值神经网络（BNNs）相比传统的32位神经网络，能够实现高达32倍的内存占用减少和58倍的推理速度提升。
现有工作
- 关于使用BNN进行HAR的研究还较少，现有的工作[13][14][15]主要采用了经典的二值卷积神经网络用于HAR任务。
- 已有不少研究尝试在基于传感器的 HAR 中引入轻量级 Transformer 架构。
- Transformer 的二值化已经被引入 NLP 和 CV 领域中，然而将二值化与 Transformer 结合用于 HAR 的研究尚未见。
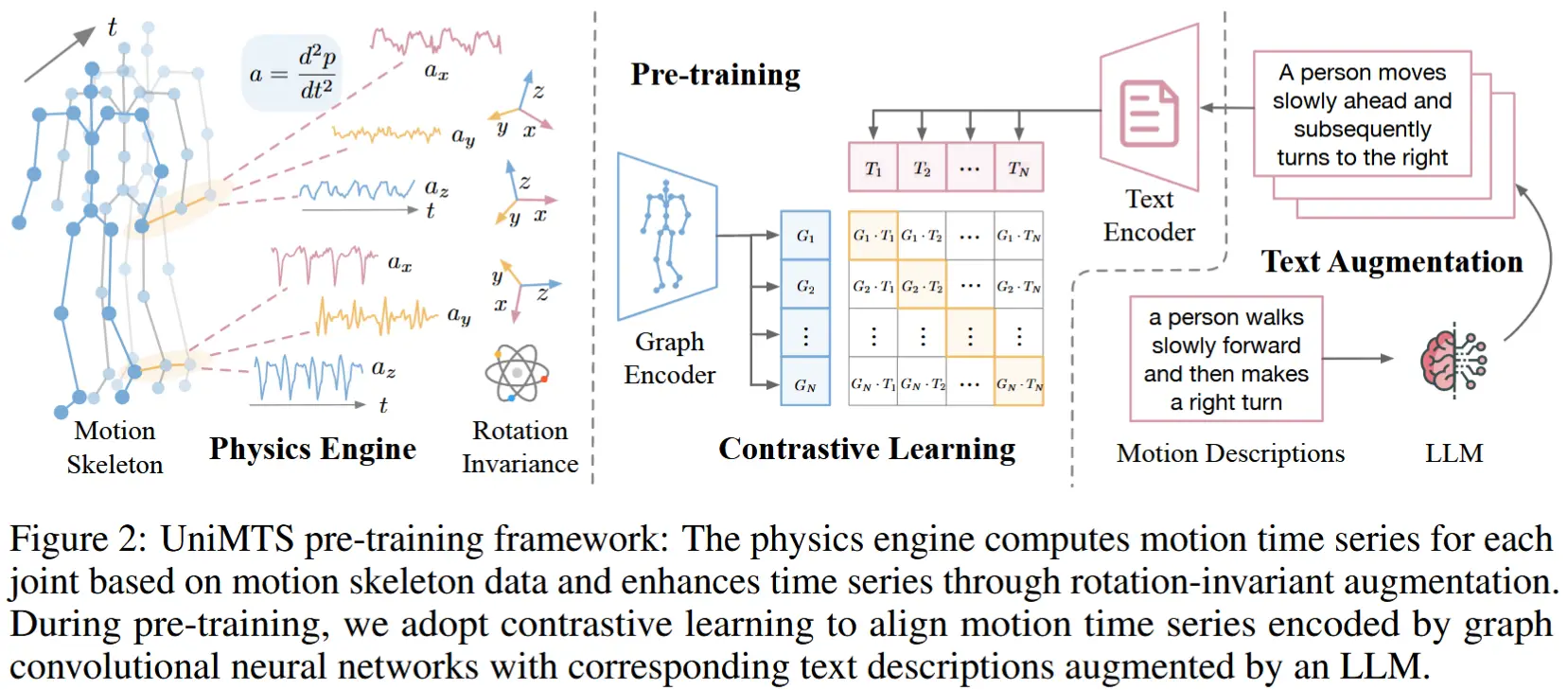
本研究中，作者对视觉 Transformer 进行了二值化处理，用于对人体活动传感器数据生成的小波频谱图进行分类。具体来说：
- 首先，对原始传感器信号进行了小波变换；
- 然后将多个通道和传感器生成的小波频谱图进行叠加，以融合传感器数据；
- 接着，我们应用了三种不同的二值化方法对 DeepViT 模型进行处理并进行了对比；
- 此外，作者深入分析了 Transformer 网络不同组件的二值化效果，这是此前未被研究的内容；
- 最后，采用了“潜层二值化”策略，即先训练全精度模型若干轮次，再切换为量化感知训练。

2 相关工作

Transformer 用于基于传感器的 HAR。例如：
- 在 [30] 中，作者提出了 Two-stream Transformer Network（TTN），通过双流结构从传感器数据中提取互补的时间和空间信息，从而提升多模态 HAR 的性能；
- 在 [31] 中，研究人员构建了一个基于 Transformer 和对抗学习原理的 HAR 框架，用于可穿戴设备中的活动识别；
- 在 [32] 中，作者设计了一种结合 CNN 与 Transformer 的混合架构，旨在同时捕捉空间细节和长时序依赖关系，以提高活动分类的鲁棒性。
- 上述研究表明，Transformer 在 HAR 领域已展现出卓越的表现。
二值神经网络（Binary Neural Networks）
- 二值神经网络（BNNs）作为量化的极端形式，尽管结构简单，却已展现出令人印象深刻的效果。
- 研究人员已经将 BNN 应用于基于传感器的 HAR 中：
  - 在 [13] 中，作者提出了一种基于 BNN 的 HAR 系统，专门针对 RISC-V 架构设计。该系统优先考虑能效和内存占用的优化，适用于低功耗设备上的实际 HAR 场景；
  - 在 [35] 中，作者提出了一种新的混合 BNN 架构，并将其部署在 Xilinx Artix-7 FPGA 上。在两个公开传感器数据集上的评估表明，该 BNN 可以实现高精度的 HAR；
  - 在 [15] 中，作者设计了一种名为 EdgeActNet 的 BNN，用于基于雷达点云数据的 HAR，该模型在两个点云数据集上达到了当前最先进的性能。
- 但是HAR领域中的BNN实现主要集中在 DNN 和 CNN 架构上，其他结构如Transformer 尚未被探索。

3 方法

基于传感器的HAR包括三个主要阶段：数据采集、数据处理和活动分类模型。本文方法主要应用于后两个阶段。

数据处理阶段：使用连续小波变换（CWT）将传感器信号转换为频谱图，并将多个传感器的频谱图进行堆叠，以实现多传感器数据融合。
活动分类阶段：采用名为 DeepViT 的 Transformer 模型对不同活动对应的小波频谱图进行分类。为了压缩模型并提升其效率，应用了三种二值化技术：Basic Binarization、Libra Parameter Binarization、Uniq Binarization，并对二值化后的模型性能进行了比较。

3.1 基于小波频谱的传感器融合

与传统的傅里叶变换不同，连续小波变换（CWT） 在精确定位信号中高频特征的时间点方面表现出色。这一优势源于其使用了类似于“小波”的局部函数，这些函数非常适合识别短暂的现象。该变换涉及在不同尺度和位置上计算信号与小波之间的内积，本质上衡量它们的相似程度。数学上，这一过程表示为：

W_s(a, b) = \int_{-\infty}^{\infty} s(t) \psi_{a,b}^*(t) dt, \tag{1}

其中，s(t) 表示连续信号，\psi_{a,b}(t) 是小波函数，变量 a 和 b 分别表示尺度参数和平移参数，即：

\psi_{a,b}(t) = \frac{1}{\sqrt{a}} \psi \left( \frac{t - b}{a} \right), \tag{2}

其中因子 \sqrt{a} 用于确保在不同尺度级别上能量表示的一致性。

通过将 (2) 式代入 (1) 式，我们可以推导出 CWT 的定义：

W_s(a, b) = \frac{1}{\sqrt{a}} \int_{-\infty}^{\infty} s(t) \psi^* \left( \frac{t - b}{a} \right) dt. \tag{3}

W_s(a, b) = \frac{1}{\sqrt{a}} \int_{-\infty}^{\infty} s(t) \psi^* \left( \frac{t - b}{a} \right) dt. \tag{4}

通过平方 WT 的幅度得到的小波频谱图，揭示了信号在整个时频平面的能量分布，有效地突出了信号中特定频率成分随时间出现的位置：

|W_s(a, b)|^2 = \left| \frac{1}{\sqrt{a}} \int_{-\infty}^{\infty} s(t) \psi^* \left( \frac{t - b}{a} \right) dt \right|^2. \tag{5}

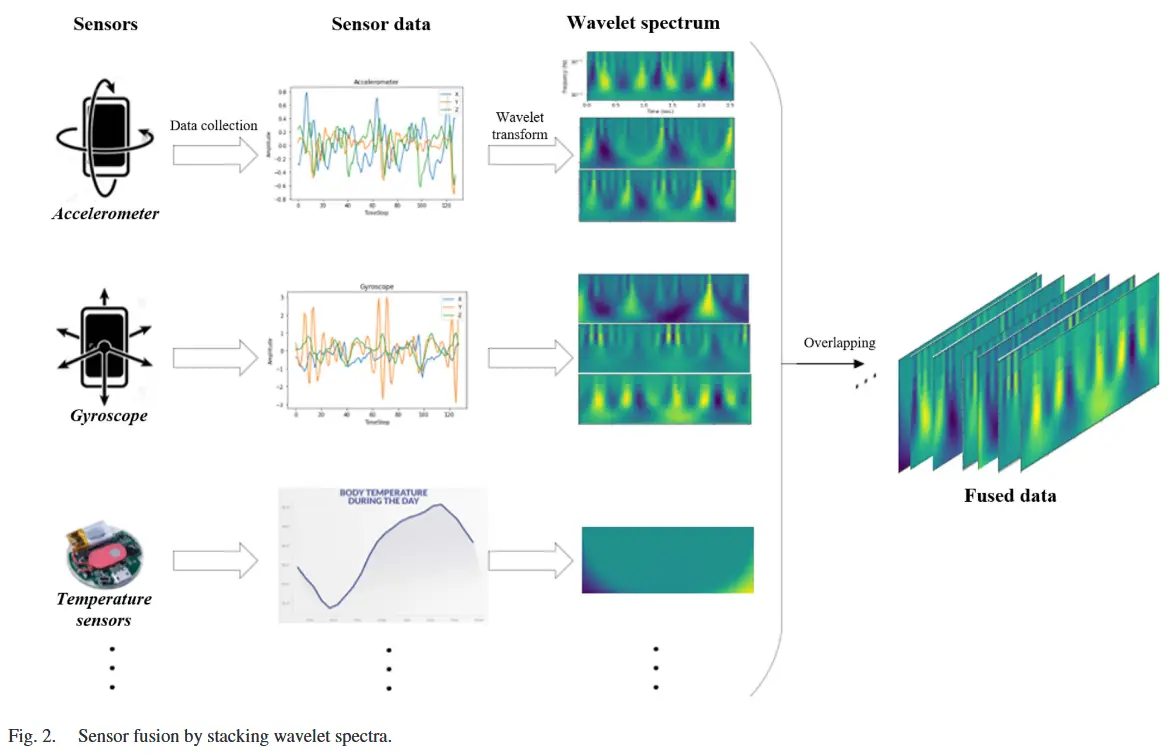
对于多传感器或多通道数据，这将产生多个频谱。我们可以通过沿“通道轴”叠加这些频谱来融合信息，从而实现数据的融合。如图 2 所示，通过叠加各自的小波频谱，我们可以创建一个类似于图像的“融合数据”结构。与 RGB 图像类似，融合数据的通道数量取决于传感器的数量及其各自的通道大小。这种融合后的数据可以直接输入到神经网络中进行训练和推理。

3.2. DeepViT

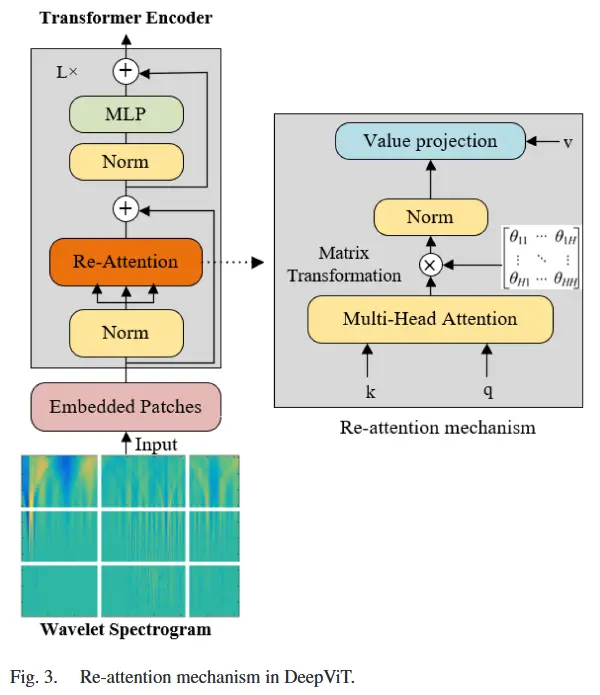
仅通过简单的块堆叠或嵌入扩展来扩展 Transformer 的规模，在没有大量数据和高级增强技术的情况下，通常难以取得显著效果。而DeepViT 解决了 Transformer 的一个重要限制，即“注意力坍塌”问题，使其能够有效扩展到更大的深度。这是通过一种新颖的自注意力机制——Re-attention 实现的。

如图 3 所示，Re-attention 动态地在不同注意力头之间交换信息，使深层 Transformer 能够再生注意力图并实现更优性能。DeepViT 利用其头部注意力图的集体智慧，动态地将它们融合成一组新的注意力图。为了细化多头注意力输出，应用了一个可训练的变换矩阵 \Theta \in \mathbb{R}^{H \times H} 。该矩阵混合了注意力图，生成新的表示形式，然后进行乘法运算。Re-attention 的公式如下：

\text{Re-Attention}(Q, K, V) = \text{Norm}\left(\Theta^\top \left(\text{Softmax}\left(\frac{QK^\top}{\sqrt{d}}\right)\right)\right)V, \tag{10}

其中，变换矩阵 \Theta 沿着头部维度对自注意力图 A 进行变换，它在整个训练过程中是可学习的。

在这项工作中，作者采用 DeepViT 进行基于传感器的HAR，因为 DeepViT 在参数较少的情况下优于多种类型的 Transformer，并在 ImageNet 数据集上达到了SOTA。

3.3 神经网络二值化

本节将介绍三种典型的二值化技术。

3.3.1 基础二值化

基础二值化旨在使用仅两个值（通常是 -1 和 +1）来表示数值数据，即将浮点权重和激活值转换为单比特表示。数学上，二值化可以表示为：

Q_x(x) = \alpha B_x, \tag{11}

其中，x 表示浮点权重 w 和激活值 a ， B_x \in \{-1, +1^n\} 表示二值权重和激活值。 \alpha 表示用于二值元素的标量，包括权重的 \alpha_w 和激活值的 \alpha_a 。 B_x 通常通过符号函数生成：

B_x = \text{sign}(x) = \begin{cases} +1, & \text{if } x \geq 0 \\ -1, & \text{otherwise}. \end{cases} \tag{12}

前向传播中的向量乘法可以表示为：

z = Q_w(w)^\top Q_\alpha(a) = \alpha_w \alpha_a (B_w \odot B_a), \tag{13}

其中， \odot 表示具有按位异或（XNOR）和计数（Bitcount）操作的向量内积。

然而，符号函数的导数为零，这使其无法与反向传播兼容。为了应对这一问题，Bengio [42] 探索了各种梯度估计技术的有效性。他发现，“直通估计器”（STE）是最佳选择。STE 通过直接在反向传播过程中传递连续梯度（通过 Identity 或 Hardtanh 函数）优雅地解决了二值化的困境。这种看似简单的策略带来了显著的结果，明显超过了其他方法设定的训练速度基准。因此，反向传播可以公式化为：

\frac{\partial l}{\partial r_i} = \frac{\partial l}{\partial r_o} 1_{|r_i| \leq t_{clip}}, \tag{14}

其中， l 表示损失， r_i 表示实数值输入， r_o \in \{-1, +1\} 表示二值输出，使用阈值梯度裁剪。

缺点：在前向传播中的符号函数和反向传播中的梯度近似严重限制了神经网络的表达能力和准确性。

3.3.2 Libra 参数二值化

许多传统的二值化模型通过最小化二值化误差来寻找最优的二值化器：

\min J(B_x(x)) = \|x - B_x(x)\|^2, \tag{15}

其中， x 表示全精度参数， B_x(x) 表示二值化参数。然而，仅仅最小化二值化误差不足以实现最优的 BNN 性能。

与传统的通过最小化二值化误差来优化的方法不同，Libra-PB 在训练过程中优先保留信息，从而实现高精度的二值化模型。Libra-PB 提供了一种新颖的前向传播方法，通过联合优化信息保留和二值化精度。假设一个随机变量 c \in \{-1, +1\} ，它遵循伯努利分布，分别以概率 p 和 1-p 取值为 -1 或 +1，其中 p \in (-1, 1) 。本质上，集合 B_x 中的每个元素可以被视为随机变量 c 的单个样本。公式 (11) 中 Q_x(x) 的熵可以数学表示为：

\mathcal{H}(Q_x(X)) = \mathcal{H}(B_x) = -p \ln(p) - (1-p) \ln(1-p). \tag{16}

新的目标函数结合了二值化误差和二值结果的信息熵，公式化为：

\min J(Q_x(x)) - \lambda \mathcal{H}(Q_x(x)). \tag{17}

为了稳定地训练 BNN，权重需要进一步平衡和归一化，通过这两步过程，获得了标准化的平衡权重 \hat{w}_{std} ：

\hat{w}_{std} = \frac{\hat{w}}{\sigma(\hat{w})}, \quad \hat{w} = w - \bar{w}, \tag{18}

其中， \sigma(\cdot) 表示标准差。Libra-PB 通过引入一个新的整数位移标量 s 来解决最小化二值化误差和昂贵浮点计算的挑战。数学上表示最优位移为：

B_w^*, s^* = \underset{B_w, s}{\text{argmin}} \|\hat{w}_{std} - B_w \ll \gg s\|^2, \tag{19}

其中， \ll \gg 表示左移或右移操作， B_w^* = \text{sign}(\hat{w}_{std}) 。因此， s^* 可以公式化为：

s^* = \text{round}\left(\log_2\left(\|\hat{w}_{std}\|_1 / n\right)\right), \tag{20}

其中， n 表示维度， \|\hat{w}_{std}\|_1 表示向量的 L1 范数。

因此，Libra-PB 的前向传播可以公式化如下：

Q_w(\hat{w}_{std}) = B_w \ll \gg s = \text{sign}(\hat{w}_{std}) \ll \gg s, \tag{21}

Q_a(a) = B_a = \text{sign}(a). \tag{22}

3.3.3 UniQ 二值化

UniQ 引入了一种适用于多比特和二值化神经网络的新型统一量化框架。它解决了现有方法的两个关键限制：权重范围变换过程中的知识损失以及对梯度消失/爆炸的敏感性。这一目标是通过独特的对称量化器和最优初始化实现的，从而最小化均方量化误差以获得更优性能。

可学习的对称量化器

假设一个量化器 Q: \mathbb{R} \to \mathbb{R} 是分段常数函数，将输入值分配到特定区间内的对应输出值。这些区间的边界称为决策电平，而分配的输出值称为重构电平。一种特殊的量化器，称为均匀量化器，具有等间距的决策电平和重构电平。这些区间的大小被称为step size，用 \Delta 表示。此外，重构电平的数量由 N 表示。量化器使用了一个裁剪函数，表示为 \text{clip}_N(x) = \min(\max(x, 0), N-1) 。四舍五入函数表示为 [\cdot] 。因此，权重通过均匀对称量化器进行量化：

Q_w(x) = \left[\text{clip}_N\left(\frac{x + a}{\Delta}\right)\right] \Delta - a, \tag{23}

其中， a = \Delta \cdot (N-1)/2 。公式 (23) 可以重写为：

Q_w(x) = \hat{q}_w(\Delta/2), \tag{24}

其中， \hat{q}_w = 2 \left[\text{clip}_N\left(\frac{x + a}{\Delta}\right)\right] - N + 1 ； \hat{q}_w 可以用 \lfloor \log_2 N \rfloor 位表示，通过将每个值编码为 +1 或 -1。

受 ReLU 中零激活频繁出现的启发，利用零值作为重构电平，并定义激活函数如下：

Q_a(x) = \left[\text{clip}_N\left(\frac{x}{\Delta}\right)\right] \Delta. \tag{25}

均匀量化器提供了调整步长 \Delta 的潜力，允许其在训练过程中动态调整以最小化任务特定的损失。由于四舍五入函数几乎处处为零的导数，其精确导数对于学习目的提供的帮助有限。为了规避零梯度问题，我们采用了直通估计器（STE），它近似为常数导数 1。

最优 MSE 初始化

为了充分利用预训练模型的知识，量化网络通常继承其初始权重，并根据统计特性调整可学习的步长。为了最小化量化引入的均方误差（MSE），需要寻找最优步长 \Delta ，并仔细考虑输入随机变量 X 的概率密度函数（pdf）。

\Delta_w^* = \underset{\Delta}{\text{argmin}} D_w(\Delta), \tag{27}

其中， D_w(\Delta) 等于 \mathbb{E}[(x - Q_w(x; \Delta))^2] 。应用莱布尼茨积分规则得到 D_w 的导数，表示为：

\frac{\mathrm{d}D_w}{\mathrm{d}\Delta} = \sum_{i=1}^{\frac{N}{2}-1} (2i-1) \int_{(i-1)\Delta}^{i\Delta} 2 \left(x - \left[\frac{2i-1}{2}\right]\Delta\right) p(x) \, \mathrm{d}x \\ - (N-1) \int_{(\frac{N}{2}-1)\Delta}^\infty 2 \left(x - \left[\frac{N-1}{2}\right]\Delta\right) p(x) \, \mathrm{d}x. \tag{28}

将公式 (28) 设为零可以揭示最优步长的路径。为了避免数值方法，我们预先计算了高斯分布和拉普拉斯分布的步长，假设单位方差和缩放。这种实现专注于高斯权重。我们使用符号 \Delta_w^u 和 \Delta_a^u 分别表示分配给权重和激活的预计算步长。因此，我们得到：

\Delta_w^* = \Delta_w^u \cdot \text{Std}(X), \tag{29}

\Delta_a^* = \Delta_a^u \cdot \sqrt{2 \mathbb{E}[X^2]}. \tag{30}

\sqrt{2 \mathbb{E}[X^2]} 是预激活的标准差。量化器输入统计量通过分析样本数据进行近似。

4 实验

4.1 实验设定

指标：准确率、内存占用、计算成本（BOPs （位操作数））
多模态传感器数据集：MHEALTH、UCI-HAR、USC-HAD
实验方法：首先在每个数据集上对 DeepViT 模型进行微调，建立一个基线性能基准。随后，将三种二值化方法分别应用于 DeepViT 模型，得到了三种二值化版本，称之为 Bi-DeepViTs 。

4.2 评估

首先在三个数据集上训练得到Bi-DeepViT，并且使用不同的超参数。每个数据集按照7：3分成训练集和测试验证集。
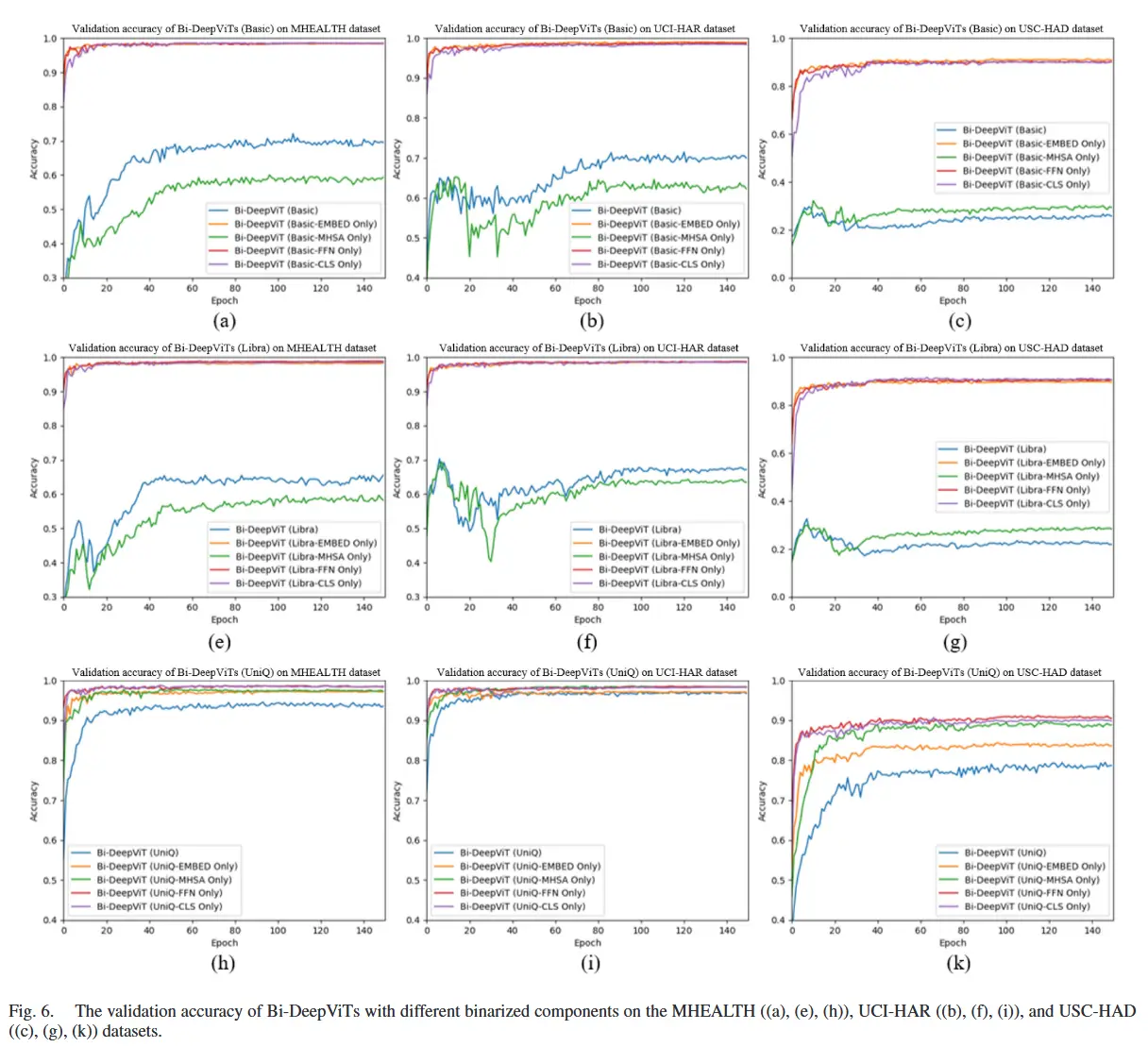
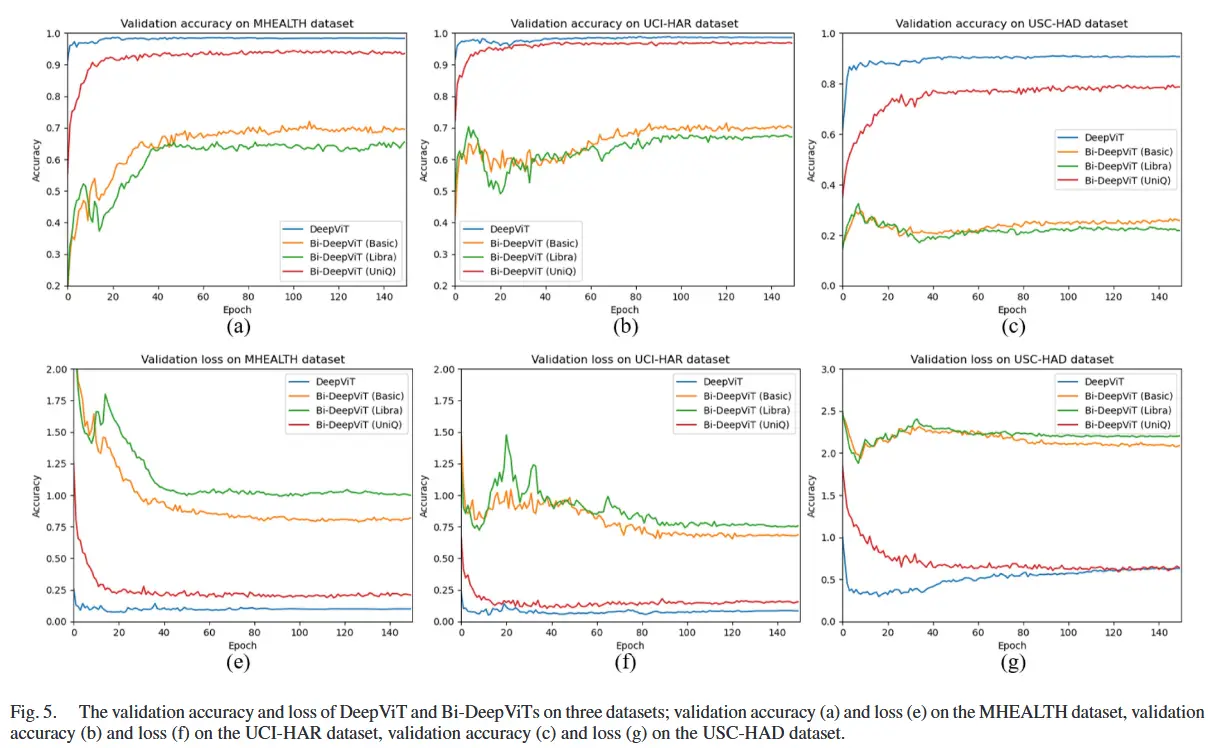
图 5 显示了 DeepViT 及其三种二值化版本在验证集上的准确率和损失变化曲线。
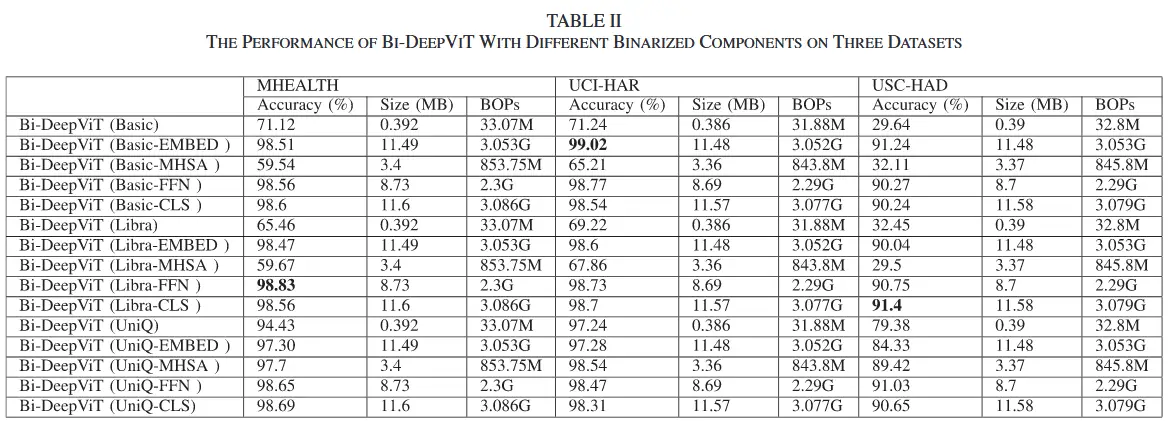
表 I 展示了这四种模型在测试集上的性能表现。
可以看到二值化后，内存占用和计算成本大幅下降，准确率也有所下降，相比之下UniQ方法性能下降最小。

4.3 消融实验

ViT由以下组件组成：patch嵌入层EMBED、Transformer 编码器堆栈（包括MHSA和FFN）、分类层CLS。
图 6 显示了在三个数据集上，对不同组件进行二值化后的 Bi-DeepViT 在验证集上的准确率变化曲线。
表 II 展示了这些模型在测试集上的具体性能表现。

论文笔记《Bi-DeepViT: Binarized Transformer for Efficient Sensor-Based Human Activity Recognition》