论文 - 《TinyHAR: A Lightweight Deep Learning Model Designed for Human Activity Recognition》
代码 -Github
关键词 - 高效、边缘智能、人类活动识别HAR、惯性传感单元IMU、卷积+Transformer

摘要

本文工作
- 设计了一款更为轻量化的模型——TinyHAR。
- 该模型专为人类活动识别任务设计，通过利用多模态数据的差异化显著性、多模态协同机制以及时序信息提取技术来实现优化。

1 背景与动机

背景
- 深度学习模型些模型通常需要大量计算资源，导致其在边缘设备上的部署效率低下。
- 深度学习模型的优异性能高度依赖大规模数据集以避免过拟合，然而数据标注的高成本限制了可用数据量。
动机：设计高效轻量的深度学习模型。

2 相关工作

基于深度学习的HAR
- DCNN[27]首次证明了卷积神经网络（CNN）在HAR任务中的潜力，其具有优异的局部依赖特征提取能力。
- MCNN[18]提出了多分支CNN结构，探索多模态传感器数据的最优特征提取与融合方式。
- 为高效建模长程时序依赖，研究者相继将多种循环神经网络（RNN）变体引入HAR任务，并提出了多种CNN-RNN混合模型[20,21,30]。
  - DeepConvLSTM[21]率先采用CNN子网络从不同传感器模态提取局部特征，再将特征输入长短期记忆网络（LSTM）。
- 近年来，基于自注意力机制的模型[26]在长时序依赖建模上展现出优于RNN的性能，相关研究也开始探索注意力机制在HAR中的应用[17,19]。
轻量化HAR深度学习模型
- 文献[4,22]尝试通过优化通道数或LSTM层数实现轻量化。
- 文献[15]尝试在CNN模型中采用分组卷积，但优化后模型参数量仍超50万。

3 方法

3.1 高效HAR模型设计准则

G1：增强局部时序上下文提取
自然语言处理中每个单词都具有语义不同，而时序数据中单个时间点的数值信息有限。
G2：差异化处理多传感器模态
不同传感器类型和佩戴位置构成的模态对活动识别的贡献度存在差异。某些模态仅对特定活动具有判别性，而其他模态可能包含无关噪声。
G3：多模态协同融合
人类活动通过身体各部位的协同运动实现。若特征提取时忽略模态间交互作用，将限制模型性能。
G4：全局时序信息提取
传感器读数中嵌入的人类活动信息具有时序动态特性，某些时间步可能展现出比相邻时段更显著的模式特征。
G5：合理压缩时序维度
过长的时序会阻碍全局依赖关系的有效提取，适当压缩时序维度既可缓解该问题，又能降低计算成本。

3.2 TinyHAR

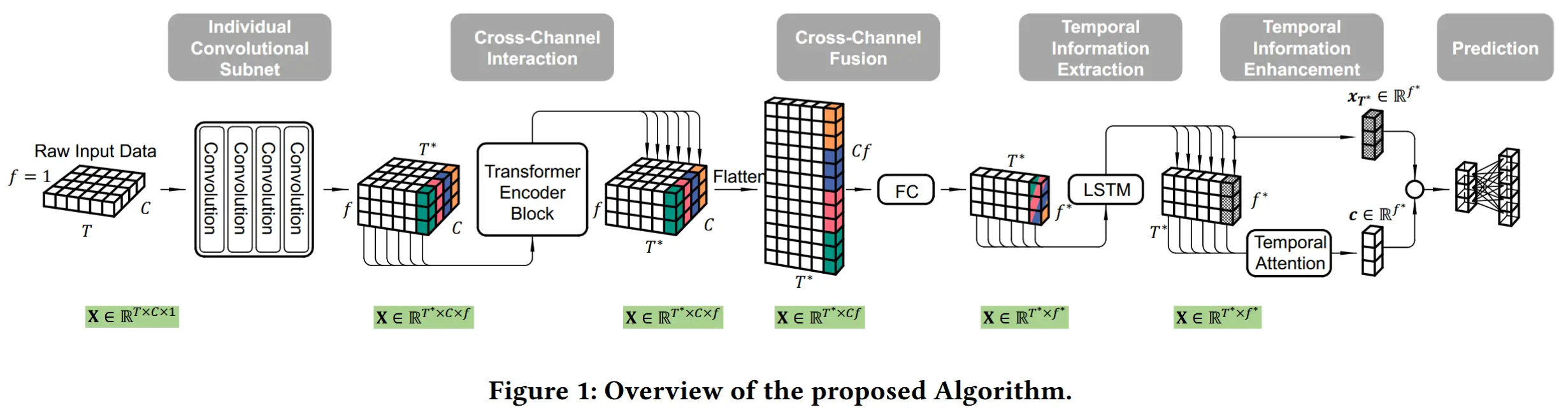
根据图1可知，TinyHAR 由五个部分组成。

模型的输入数据为 X \in \mathbb{R}^{T \times C \times F} ，其中 T - 时间滑动窗口大小， C - 传感器通道的数量， F - 滤波器的数量。

3.2.1 单独卷积子网

为了增强局部上下文，应用了一个卷积子网来从原始数据中提取和融合初始局部特征（G1）。考虑到不同模态的贡献差异，每个通道通过四个单独的卷积层分别进行处理（G2）。单独卷积意味着内核在时间轴上仅具有 1D 结构（内核大小为 5 \times 1 ）。为了减少时间维度（G5），每层的步幅设置为 2。所有四个卷积层具有相同的滤波器数量 F 。该卷积子网的输出形状为 \mathbb{R}^{T^* \times C \times F} ，其中 T^* 表示减少后的时间长度。

3.2.2 Transformer 编码器：跨通道信息交互

受 [1] 启发，本文利用一个 Transformer 编码器块来学习每次时间步长上的跨传感器通道维度的交互（G2）。Transformer 编码器块由一个缩放点积自注意力层和一个两层全连接前馈网络组成。缩放点积自注意力用于根据每个传感器通道与其他所有传感器通道的相似性确定其相对重要性。随后，**每个传感器通道利用这些相对权重聚合来自其他传感器通道的特征。**然后，前馈层应用于每个传感器通道，进一步融合了每个传感器通道的聚合特征。到目前为止，每个通道的特征已经与底层的跨通道交互进行了上下文关联。

3.2.3 全连接层：跨通道信息融合

为了融合来自所有传感器通道的学习特征（G3），首先将这些表示在每个时间步长上向量化，从 X \in \mathbb{R}^{T^* \times C \times F} 转换为 X \in \mathbb{R}^{T^* \times CF} 。然后，应用一个 FC 层对所有特征进行加权求和，FC 层允许同一传感器通道的不同特征具有不同的权重，带来了更充分的特征融合。此外，这个 FC 层在提出的 TinyHAR 中还充当瓶颈层，将特征维度降低到 F^* （设置 F^* = 2F ）。

3.2.4 单层 LSTM：全局时间信息提取

在传感器和滤波器维度的特征融合之后，获得了一组精炼的特征向量序列 \in \mathbb{R}^{T^* \times F^*} ，可用于序列建模。然后，应用一个 LSTM 层来学习全局时间依赖关系。

3.2.5 时间注意力：全局时间信息增强

由于并非所有时间步长对正在进行的活动识别的贡献相同，因此学习序列中每个时间步长特征的相关性至关重要。遵循 [16] 中的工作，通过计算每个时间步长隐藏状态（特征）的加权平均值生成全局上下文表示 c \in \mathbb{R}^{F^*} 。权重通过时间自注意力层计算。因为最后一个时间步长的特征 x_{T^*} \in \mathbb{R}^{F^*} 包含整个序列的表示，所以生成的全局表示 c 被添加到 x_{T^*} 中。在这里，引入了一个可训练的乘法参数 \gamma 作用于 c ，这使得模型能够灵活地决定是否使用或丢弃生成的全局表示 c 。

论文笔记《TinyHAR: A Lightweight Deep Learning Model Designed for Human Activity Recognition》

摘要