论文 - 《MobHAR: Source-free Knowledge Transfer for Human Activity Recognition on Mobile Devices》
代码 - Github
关键词 - Ubicomp2025、域适应DA、Gram矩阵、人类活动识别HAR

摘要

研究问题：人类活动识别HAR通常数据分布是非独立同分布的。现有的领域自适应（DA）方法试图解决这一问题，但它们要么需要访问源域数据，要么在面对较大的领域差异时表现不佳。
本文工作
- 本文提出了一种新颖的无源域自适应框架 ，专门用于解决HAR任务中不同数据集之间的显著领域差异。包含以下两个关键创新点：
  - （1）一种判别信息Gramian矩阵 （Discriminative Information Gramian, DIG）方法，能够在不访问源域数据的前提下，量化目标域样本与源域之间的关系；
  - （2）一种无监督领域泛化技术 ，确保在增强后的数据样本上提取出一致的特征，从而提升模型在目标域中的有效性。
意义：本研究是首次成功实现无需源数据的、面向数据集级别的人类活动识别领域自适应方法 ，标志着在实际HAR应用方面的重要进展。

1 引言

HAR上域适应的相关工作
- 第一类：例如 UniHAR 和 CrossHAR，仅利用源域数据来做适应。它们通常采用基于对齐的方法，使从新用户数据中提取的特征尽可能接近源域特征，从而实现模型自适应。然而，实际中源域数据往往无法访问。
- 第二类：例如 OFTTA 和 SF-Adapter，仅使用目标域数据实现自适应。它们通常采用自监督学习策略，强制模型能够聚类为结构与真实标签相似的不同类别。然而，当面对较大的领域差异（例如：跨数据集）时，其性能明显下降。
挑战
- （1）在不访问源数据的情况下，实现面向整个数据集级别的 HAR 模型自适应并同时保持良好的性能。
- （2）在缺乏目标域标签的情况下，难以对 HAR 模型进行有效的微调，以使其能够泛化到所有目标域数据。
本文解决办法 - MobHAR
- 基于 DIG 的目标域样本选择：为了选出适合域自适应的目标域样本，首先对数据进行增强，并挑选在特征空间中彼此接近的真实样本与增强样本对。通过提取模型最后一层输出作为“判别信息”，结合模型参数构建判别信息Gram矩阵（DIG），用于衡量样本之间的距离。该方法不仅反映特征间的相似性，还隐含了样本与源域之间的关系，从而有效筛选出靠近源域的高质量目标样本。
- 基于特征一致性的领域泛化策略：设计了一种无监督的模型更新机制，确保从选定样本及其增强版本中提取的特征保持一致性。具体通过计算真实样本与增强样本特征分布之间的Wasserstein 距离来衡量差异，并使用核范数 ||\cdot||_* 构建损失函数，引导模型在微调过程中提升泛化能力。

2 预备知识与动机

2.1 Source-free HAR

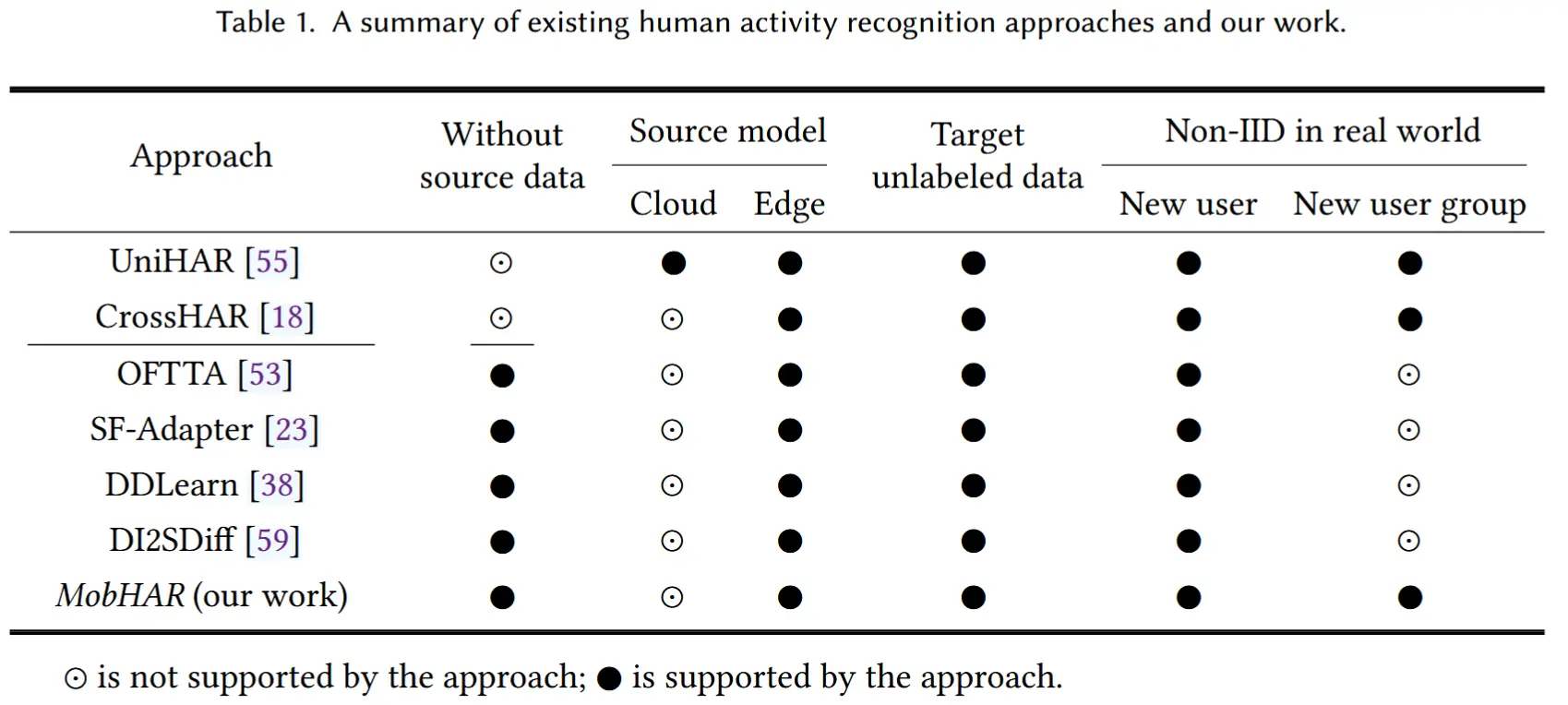
如表 1 所示，将现有的 HAR 方法分为两类：
- 基于源数据的方法：指那些需要访问模型原始训练数据的方法，例如 UniHAR 和 CrossHAR；
- 无源 HAR 方法：指那些在处理非独立同分布（non-IID）数据时不需要源域数据的方法，例如 SF-Adapter、OFTTA 等。
局限性在引言部分指出了。因此，目前尚无一种准确且适用于现实环境的活动监测方案能够同时满足隐私保护和性能需求。

2.2 现实环境中 non-IID 数据问题

现有许多 HAR 模型通常假设数据服从独立同分布。然而，由于个体差异（如年龄、体型、行为习惯等），这一假设常常不成立，从而限制了模型在其他领域上的泛化能力。例如，在 [36] 中提到的 ASTTL 方法在跨数据集迁移时平均准确率仅为 66.3%，说明在面对大规模分布偏移时性能下降严重。

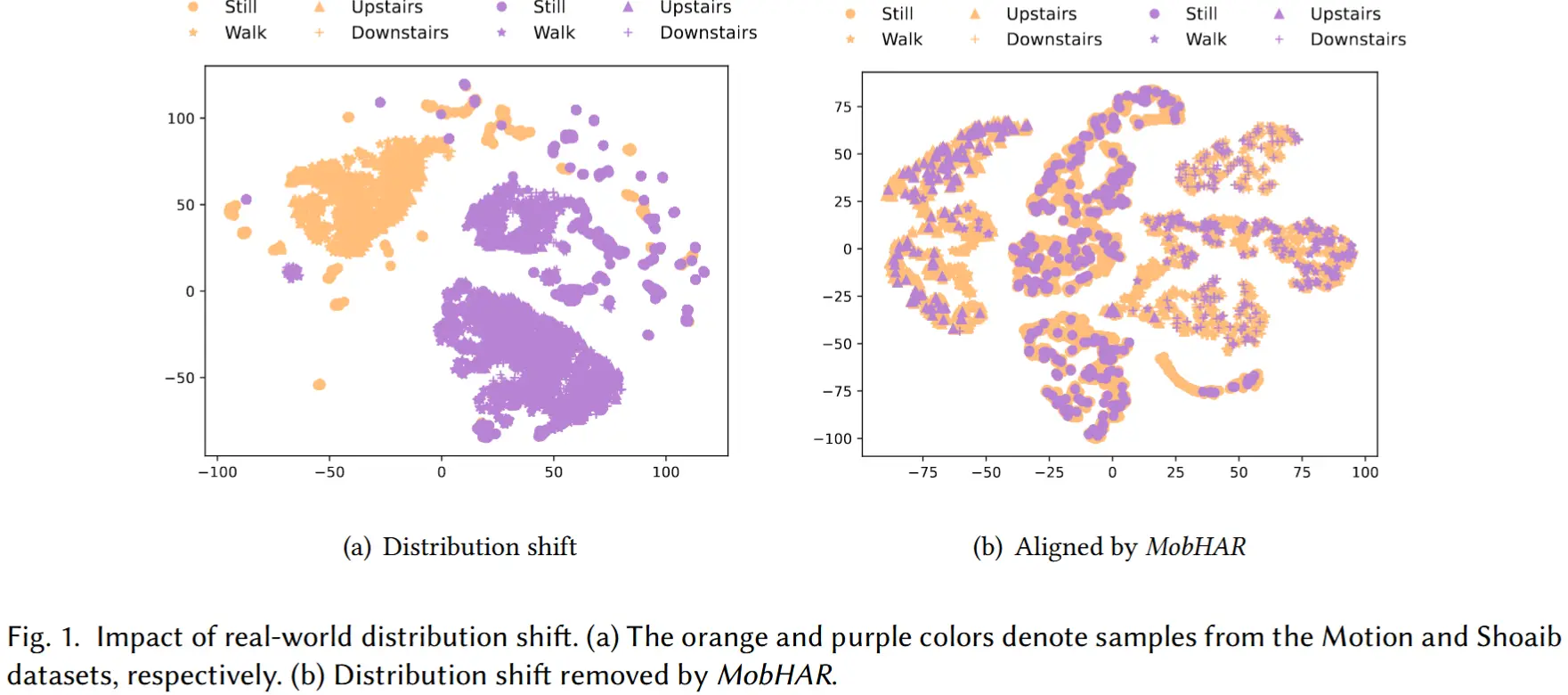
为了直观展示不同数据集之间的分布偏移情况，作者使用 t-SNE 对 Motion 和 Shoaib 数据集中的 IMU 数据进行可视化，结果如图 1(a) 所示。可以看出，即使是相同的活动类型，在两个数据集中所对应的 IMU 数据特征也存在显著差异。

为了初步评估 MobHAR 在处理分布偏移方面的能力，作者在将 Shoaib 数据迁移到 Motion 数据后，对样本特征进行了 t-SNE 可视化分析，结果如图 1(b)。结果显示，MobHAR 能够有效缓解分布偏移带来的影响。

2.3 问题定义

HAR 框架旨在为新用户从预训练模型中本地定制个性化模型。预训练模型是在初始数据集上训练得到的，该数据集被定义为源域 \mathcal{D}_S = \{(x_i^s, y_i^s)\}_{i=1}^{n_s}，其中 x \in \mathbb{R}^d 表示 d 维传感器输入，y \in Y 表示对应的活动标签。新用户下载预训练的 HAR 模型，并将其在一台或多台移动设备上采集的本地、无标签数据集定义为目标域 \mathcal{D}_T = \{x_i^t\}_{i=1}^{n_t}。

由于年龄、设备、身体位置、体型和行为习惯等因素的影响，目标域 \mathcal{D}_T 和源域 \mathcal{D}_S 之间的数据分布可能存在显著差异。

2.4 设计动机

测试时自适应TTA：通过使用无标签数据生成的伪标签来提升模型的泛化性能。然而，伪标签和真实标签之间不可避免存在误差，导致梯度噪声并使模型偏离正确方向，还有可能加剧这些错误，严重降低预测能力。

因此，一个自然的问题浮现出来：我们是否可以利用高质量的数据来微调模型？

根据文献 [2] 的观察：如果一个数据样本远离源域，原始 HAR 模型将给出低置信度的预测；而如果一个样本靠近源域，则该样本及其增强版本会产生一致的预测结果。

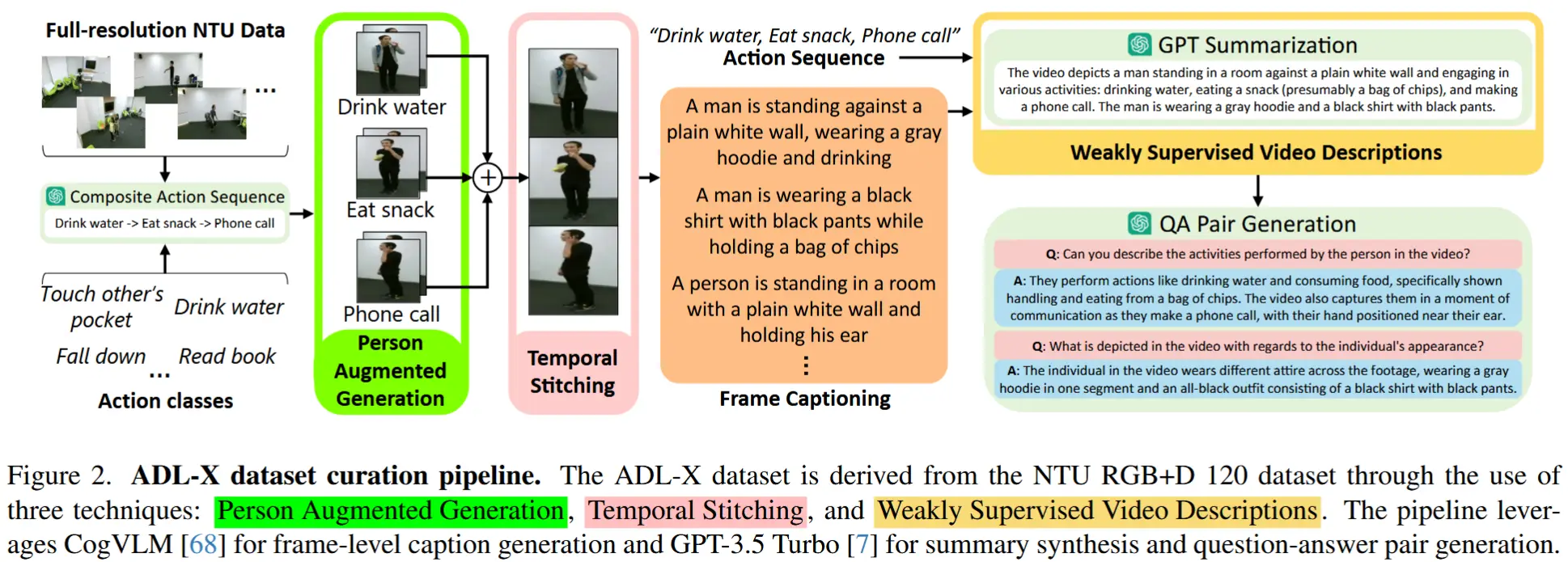
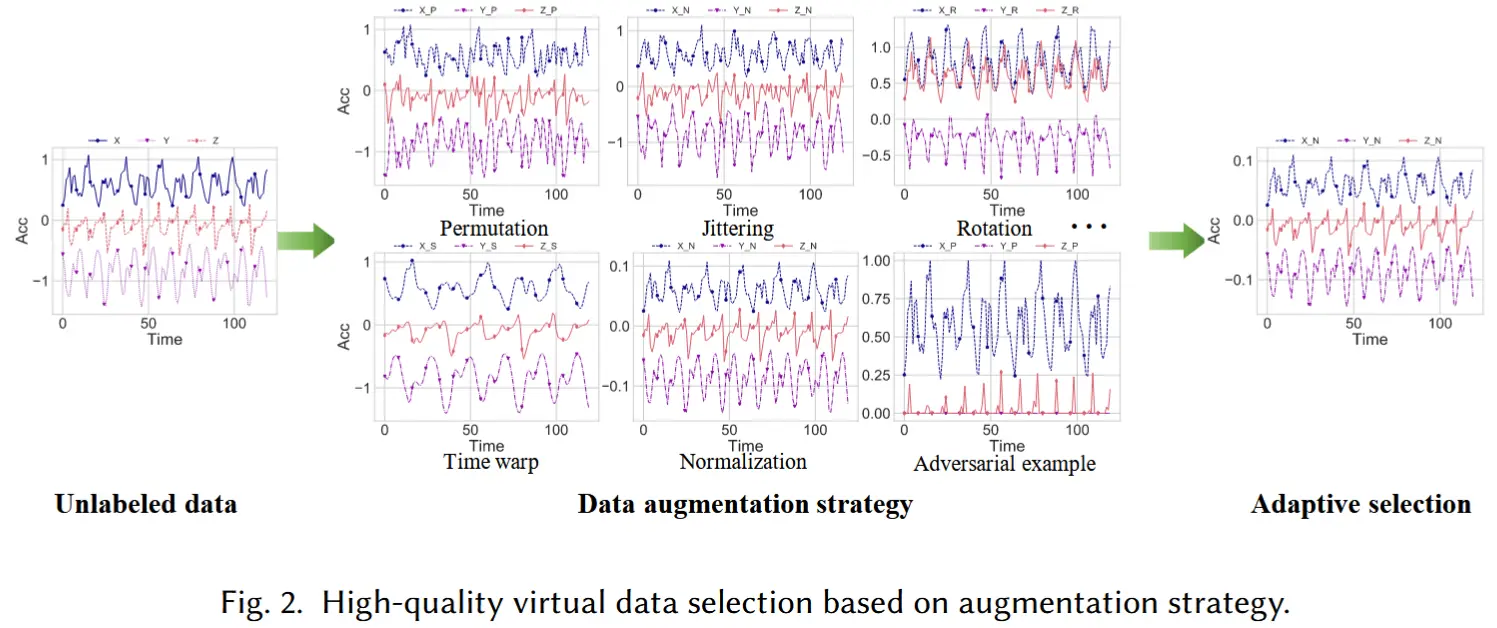
从上述观察中，作者引入了DIG方法来评估无标签数据质量，用于量化目标域数据样本与源域之间的关系。因此，如图 2 所示，对于每一个无标签数据样本：

首先采用六种数据增强策略对其进行增强，包括：归一化（Normalization）、旋转（Rotation）、包裹（Wrapping）、置换（Permutation）、对抗样本（Adversarial Examples）、抖动（Jittering）。
接着使用 DIG 方法从这六种增强策略中选择出最优的“真实-虚拟”数据对。
最后，在每个训练批次中，我们选择前10%的高质量“真实-虚拟”数据对，它们最接近源域分布、最适合用于模型优化。

3 MobHAR 的设计

如图 4 所示，MobHAR 主要由两个部分组成：计算 DIG 值+构建个性化模型。

计算 DIG 值
- 本节中，作者在特征空间的背景下设计了 DIG 方法。DIG 矩阵用于量化新用户数据与其增强版本之间的差异。通过使用 DIG 方法，可以评估高质量数据，从而定制一个无源数据的 HAR 模型。
- 因此，DIG 矩阵在以下三方面起到了关键作用：选择合适的预训练模型、实现无源知识迁移、确定早停时机以防止过拟合。
构建个性化模型
- 在本节中，作者提出了一种利用 DIG 来定制个性化模型的方法。具体而言，设计了一个对抗机制，以促进无源的知识迁移过程，从而为新用户量身打造 HAR 模型。
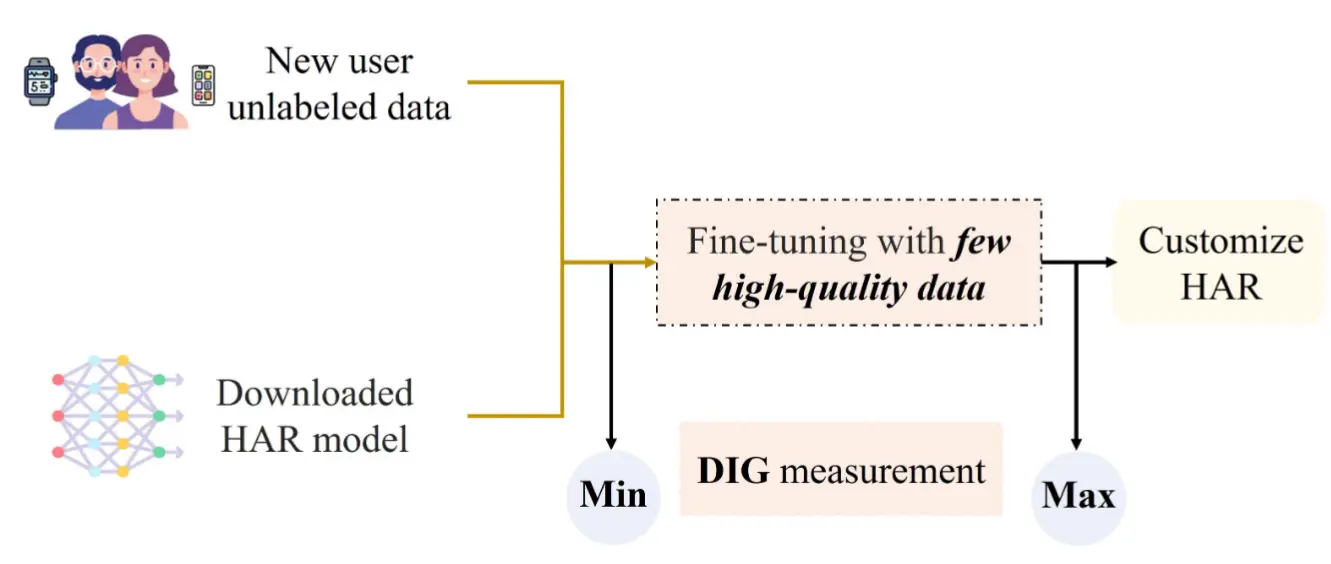
方法流程：
- （1）使用 最小 DIG 值 筛选高质量的无标签数据，并结合多种数据增强策略提升样本多样性。
- （2）在对应 最大 DIG 值的训练轮次 完成 HAR 模型的微调，此时模型在目标域上的适配性最佳。

通过这种方式，MobHAR 实现了无需访问源域数据即可完成模型自适应的目标。

3.1 基于Gramian矩阵的最大均值差异信息

3.1 Maximum Mean Discrepancy Information using Gramian Matrix(DIG)

为了尽可能保证伪标签的质量，理想情况下应消除HAR模型的训练数据（源域）与用户无标签数据（目标域）之间的分布差异。

为此，作者设计了一种基于特征空间Gramian矩阵的最大均值差异信息方法，用于筛选高质量样本，从而提升伪标签的可靠性。

具体来说，DIG包括以下几个步骤：

使用Gramian矩阵信息：首先利用Gramian信息计算从 HAR 模型各层提取的一组特征之间的内积。
构建特征空间中的Gramian表示：使用无标签数据及其增强版本在特征空间中构建Gramian表示。
提取判别信息：从统计矩中提取判别信息，并计算中位数与中位绝对偏差（median absolute deviation, MAD）。
量化样本质量：基于特征空间中的 DIG，我们量化了无标签数据与其增强变体之间的距离。总体而言，DIG 值越低，表示伪标签的质量越高。

3.1.1 HAR 模型中的Gram矩阵

Gramian信息在风格迁移学习中被广泛使用，它计算一组 m-维向量的内积。这些向量可以表示从 HAR 模型各层提取的特征。形式上，HAR 模型的一组 m-维层定义为：

\mathbf{L} := \{l_n | l_n \in \mathbb{R}^m\}_{n=1}^N, \tag{1}

其中，l_n 表示输入样本 x 在 HAR 模型第 l 层的特征表示，N 表示该层的通道数，而 m 表示每个特征图的高度乘以宽度。

因此，定义 HAR 模型的Gramian矩阵为：G_{ij} = \sum_n^m l_{in} \cdot l_{jn}^T，其中 G_{ij} 表示特征空间中维度为 N \times N 的内积空间中各层之间的Gramian信息。Gramian矩阵的 p-阶项定义为：

G_{ij}^p = (l_i^p l_j^{pT})^{1/p}, \tag{2}

其中 p 表示指数。由于矩阵 G_{ij}^p 是对称的，可以将其形成一个 N(N+1)/2 维的向量，记为 G_d^p，其中 d 表示 N(N+1)/2 的维度。

给定一个阶数上限 P，可以为每个阶数 p \in \{1, ..., P\} 导出 G_d^p。对于输入样本 x，我们通过拼接所有 G_d^p 来创建一个新的表示 r = [G_d^1, G_d^2, ..., G_d^P] \in \mathbb{R}^{dP}。令 x_t 表示未知目标用户的无标签数据样本，x_{ta} 表示其增强版本。因此，对于给定的 HAR 模型，我们可以得到拼接后的Gramian信息集合 R_t = \{r_i, i \in 1, 2, ..., |x_t|\}。类似地，我们导出增强数据样本的表示 R_{ta} = \{r_i, i \in 1, 2, ..., |x_{ta}|\}。因此，模型与新用户无标签数据之间的关系可以通过测量 R_t 和 R_{ta} 之间的距离来表达。

3.1.2 构建 DIG

令 x_t^p \sim P_{t,p} 和 x_{ta}^p \sim P_{ta,p} 分别表示来自未知目标用户分布 P_{t,p} 和用户增强分布 P_{ta,p} 的 p-阶表示。MobHAR 在不假设任何关于 P_{t,p} 和 P_{ta,p} 的先验条件下，在特征空间中计算表示。具体而言，MobHAR 从 P_{t,p} 和 P_{ta,p} 的统计矩中提取判别信息。参考文献 [29]，我们可以将 DIG 定义为统计矩的一种视角：

\text{DIG}(P_t, P_{ta}) = E_p[E(G_{x_t^p}) - E(G_{x_{ta}^p})] \\ = E_p[\mu_1^p {\mu_1^p}^T - \mu_2^p {\mu_2^p}^T + \sigma_1^p - \sigma_2^p], \tag{3}

其中 \mu_1^p 和 \sigma_1^p 表示 x_t^p 的均值向量和协方差矩阵，\mu_2^p 和 \sigma_2^p 表示 x_{ta}^p 的均值向量和协方差矩阵。P_t 表示来自未知目标用户分布的具有不同幂次元素的表示集合，而 P_{ta} 表示这些用户的增强分布集合。

详细推导过程见论文附录。

3.1.3 计算 DIG

利用未知目标用户数据 x_t 的Gramian信息 R_t = \{r_i, i \in 1, 2, ..., |x_t|\}，计算中位数和中位绝对偏差MAD，分别定义为：

\tilde{r}_j = \text{Me}(r_{ij}, i \in |x_t|) \quad \text{和} \quad \text{MAD}_j = \text{Me}(|r_{ij} - \tilde{r}_j|, i \in |x_t|).

然后，我们计算特征表示 \hat{r}_j 到候选点 \tilde{r} 的距离，公式如下：

\delta_j(\hat{r}_j) = \begin{cases} 0, & \text{if } b_l \leq \hat{r}_j \leq b_u, \\ \frac{b_l - \hat{r}_j}{b_l}, & \text{if } \hat{r}_j \leq b_l, \\ \frac{\hat{r}_j - b_u}{b_u}, & \text{if } b_u \leq \hat{r}_j, \end{cases} \tag{4}

其中，b_l = \tilde{r}_j - 10 \times \text{MAD}_j 和 b_u = \tilde{r}_j + 10 \times \text{MAD}_j 分别表示下界和上界。因此，候选点 \tilde{r} 的距离可以通过累加所有 \hat{r}_j 来计算，即：

\delta = \frac{1}{d^P} \sum_{j=1}^{d^P} \delta_j.

由于未知目标用户分布与增强分布之间可能不存在显著差异，因此在评估 R_t 和 R_{ta} 之间的距离时，必须采用一种不假设分布特性的分布测量方法。借鉴距离测量方法的最新进展 [9, 16, 31]，我们可以使用 **RMMD（Robust Maximum Mean Discrepancy）**重新表述公式 (3)，如下所示：

\text{DIG}(P_t, P_{ta}) = \|\mu_{P_t} - \mu_{P_{ta}}\|_{\mathcal{H}}^2 - \lambda_{P_t} \|\mu_{P_t}\|_{\mathcal{H}}^2 - \lambda_{P_{ta}} \|\mu_{P_{ta}}\|_{\mathcal{H}}^2, \tag{5}

其中，P_t 和 P_{ta} 表示从偏差测量中获得的两个子组（未知目标用户及其增强）的表示分布。

3.2 构建个性化模型

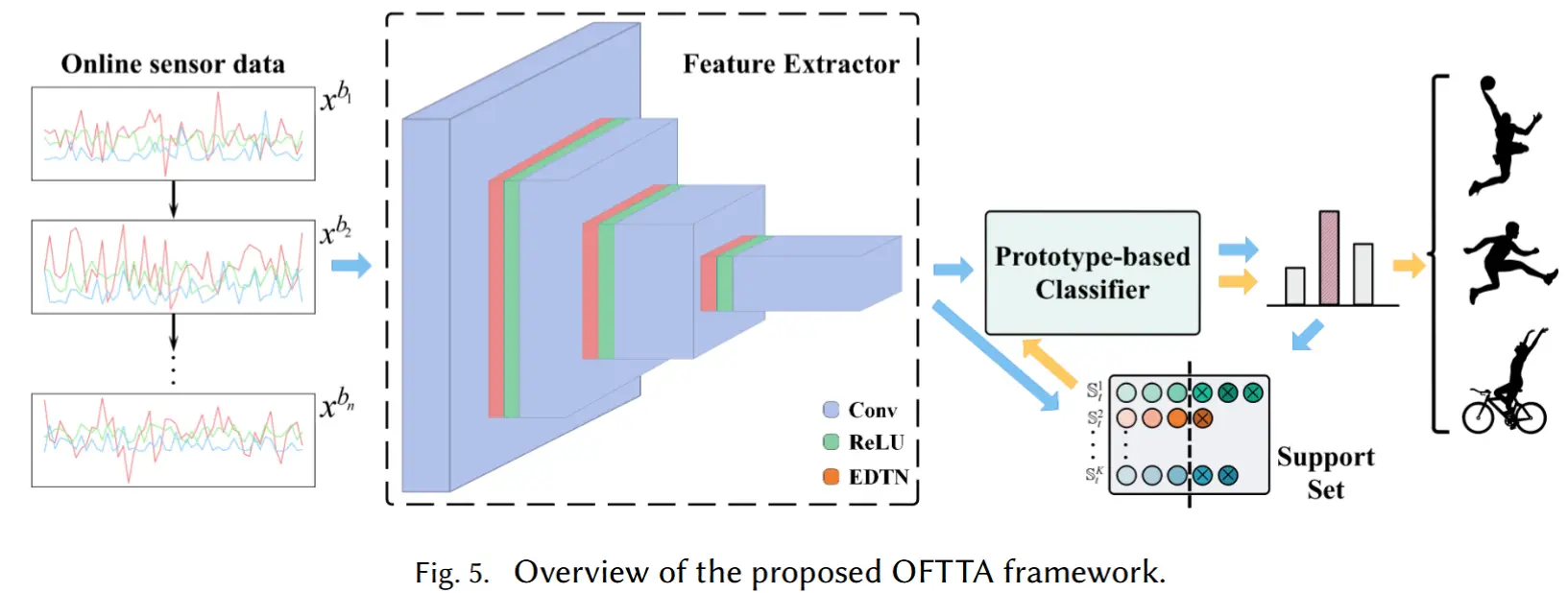
在评估通用模型与个性化模型之间的差异之后，可以利用这一信息，通过无源知识迁移来定制个性化的 HAR 模型。如图 5 所示，作者设计了一种对抗机制以促进这种无源的知识迁移。

该机制分为两个阶段：

最小化阶段：基于最小 DIG 值选择高质量的无标签数据，并用于微调 HAR 模型。包含差异度量以选择高质量数据和差异消除(3.2.1&3.2.2)。
最大化阶段：使用最大 DIG 值判断当前高质量数据是否足够完成微调任务，从而决定是否终止训练。包含防止过拟合(3.2.3)。

3.2.1 差异度量以选择高质量数据

作者利用 DIG 方法 来量化无标签数据与其增强版本之间的距离，确保 MobHAR 能够有效选择出高质量样本。

具体流程如下：

对每个样本应用多种数据增强技术。使用多种数据增强策略的原因是：某些增强操作可能会改变数据中的关键特征。
计算每对原始样本与增强样本之间的 DIG 距离，根据最小 DIG 值筛选出最接近源域的新用户数据及其变体。

选择多种增强策略的原因在于，不同的增强方式可能会影响数据中的关键特征，有助于识别哪些样本在变换后仍能保持稳定特性，从而反映其与源域的接近程度。

为了基于新用户数据及其变体进行无源知识迁移，借助 HAR 模型预测出的判别信息进行处理。具体来说，计算两个特征分布 P_t（原始样本）与 P_{ta}（增强样本）之间的 Wasserstein 距离。然而，由于新用户数据的分布复杂，Wasserstein 距离往往会错误地强调领域级特征混淆，从而削弱用户的活动信息。

根据文献 [22]，HAR 模型预测的自相关矩阵中：

主对角线元素表示类内相关性 I_i
非对角线元素表示类间混淆 I_o

对于一个未知的目标用户：如果其与预训练模型所使用的用户数据分布差异较大，则模型预测通常会产生较小的 I_i 和较大的 I_o；反之，则会产生较大的 I_i 和较小的 I_o。因此，可以使用 I_i - I_o 来衡量模型预测的稳定性，同时有助于消除分布偏移带来的影响。

3.2.2 消除差异

为了减少通用模型与个性化模型之间的差异，基于预训练的 HAR 模型 f 和一个 softmax 层作为分类器 S 构建了一个结构。由于通过 Frobenius 范数 Wasserstein 距离衡量的 I_i 和 I_o 之间的差异可能会忽略样本量较小的类别，作者使用核范数 \|\cdot\|_* 来增强预测多样性。

为了解决 HAR 模型在适应过程中需要重复交替更新的问题，引入了梯度反转层（Gradient Reverse Layer, GRL），这有助于在一个反向传播步骤中完成更新。因此，MobHAR 的无源知识迁移过程如下：

\mathcal{L}_{\theta_f} = \min \left\{ \frac{1}{N_u} \sum_{i=1}^{N_u} \left( \| S(f(x_i^t)) \|_* - \| S(f(x_i^{ta})) \|_* \right) \right\}, \tag{6}

其中，N_u 表示未知目标用户的数据样本数量，x^t 表示未知目标用户 t 的样本，x^{ta} 表示其增强数据样本。

3.2.3 防止过拟合

为了解决遇到挑战性样本时带来灾难性遗忘的问题，作者利用 DIG 来量化最大 DIG 值对应的停止时间。此外，还采用了一种随机恢复方法，从预训练模型中恢复权重，以支持长期适应。首先，我们使用一种随机恢复方法，从预训练模型中恢复权重：

W_{t+1} = M \odot W_0 + (1 - M) \odot W_{t+1}, \tag{7}

其中，M \sim \text{Bernoulli}(p)，\odot 表示逐元素乘法，W_0 表示源权重，W_{t+1} 表示可训练参数，而 M 是一个掩码张量。

为了最大化模型对新用户高质量无标签数据的利用，在移除 DIG 距离中的显著异常值后，在最大值处停止微调。如算法 1 所示，结合Gramian矩阵的差异信息与源模型的自适应，形成了 MobHAR 框架。

4 实验

4.1 实验设定

数据集：HHAR、UCI、Motion、Shoaib、USC（加速度计+陀螺仪）
评估指标：F1分数和准确率
基线：OFTTA、TAST、Tent、SAR、UniHAR、CrossHAR
实验场景：单源（从HHAR数据集迁移到其他数据集）、多源（在其他数据集训练迁移到HHAR数据集）

4.2 实验结果

多源单目标
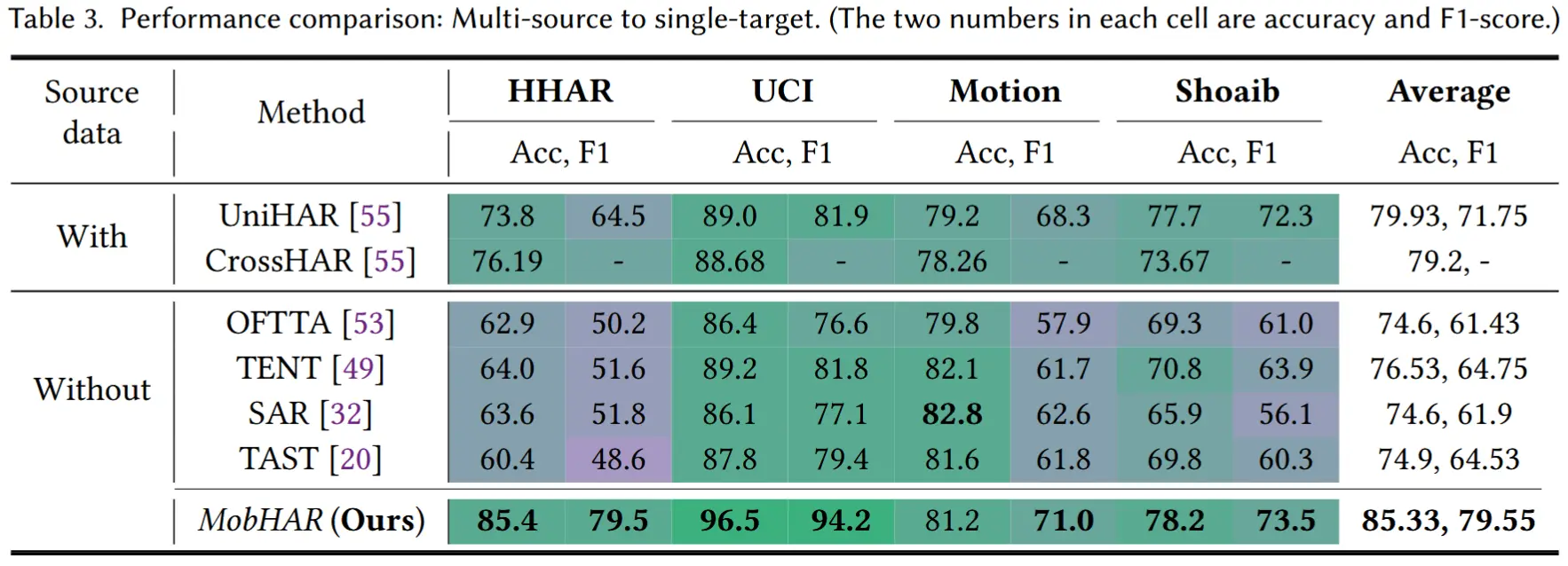
- 结果如表3所示。
- 基于源域数据的方法整体性能优于当前最先进的无源方法。
- 与无源方法相比，MobHAR 在 F1 分数上提升了 14.76% ，在准确率上提升了 8.8% 。

单源单目标
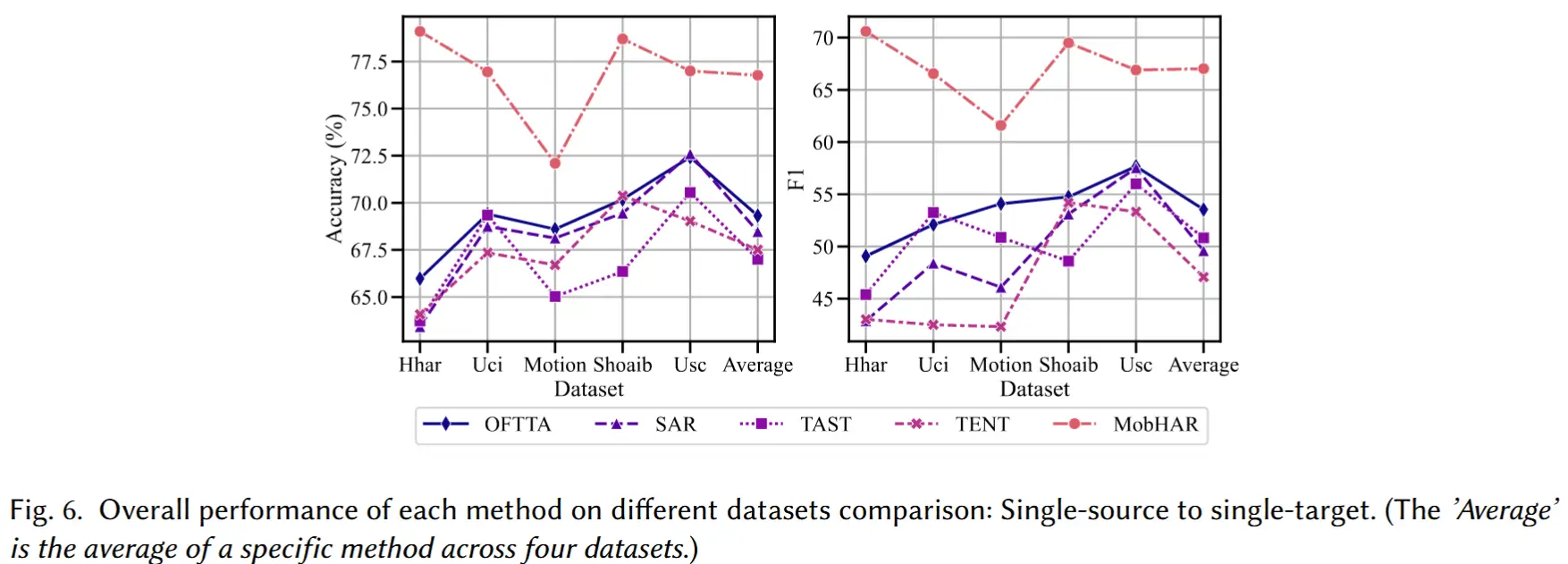
- 结果如图6所示。
- OFTTA 的性能高于其他无源方法。这是由于 OFTTA 是专门为 IMU 数据设计的，而其他无源方法主要是针对图像数据设计的。
- MobHAR 实现了 76.77% 的平均准确率和 67.03% 的 F1 分数，在 F1 分数上至少比最优基线方法高出 17.43% ，在准确率上高出 9.77%。

论文笔记《MobHAR: Source-free Knowledge Transfer for Human Activity Recognition on Mobile Devices》

摘要