论文 - 《Adaptive Keyframe Sampling for Long Video Understanding》
代码 - Github
关键词 - 自适应抽帧、多模态大模型MLLM、相关性、覆盖度、采样

1 引言

研究问题
- MLLMs 通过将视觉输入作为额外的标记注入到 LLMs 中作为上下文，然而，当视觉输入从单张图像变为长视频时，会导致视频标记的数量巨大，远远超出 MLLMs 的最大处理能力。
现有的工作和不足
- 现有的基于视频的MLLMs大多依赖于从输入数据中采样少量标记，这可能导致关键信息丢失，从而产生错误的答案。
本文工作
- 提出了一种简单而有效的算法，称为自适应关键帧采样（Adaptive Keyframe Sampling, AKS）。
- 该算法引入了一个即插即用的模块——关键帧选择，旨在在固定数量的视频标记下最大化有用信息。
- 作者将关键帧选择问题建模为一个优化问题，包含两个方面：
  1. 相关性：利用视觉-语言（VL）模型计算每个候选帧与输入提示之间的相关性；
  2. 覆盖度：通过将视频递归划分为多个区间（bins），统计每个区间内的关键帧数量，从而估计覆盖度。
- 单独最大化相关性或覆盖度可产生简单基线，而自适应关键帧采样（AKS）算法在两者之间实现合理权衡，能够实现最优的视频理解效果。

2 相关工作

LLM 和 MLLM
- 为了扩展LLMs以实现视觉理解，学术界致力于将视觉与语言数据对齐到统一的特征空间中。目前的方法主要分为两类：
  1. 内部适配（internal adaptation），例如通过在LLM内部引入交叉注意力机制来实现视觉-语言对齐；
  2. 外部适配（external adaptation），例如通过训练额外的模块来达成相同目标。
- 通过上述方法，视觉基础模型逐渐演进为 MLLMs。
基于视频的 MLLMs
- 早期工作包括 VideoChat [18]、Video-ChatGPT [26]、VideoLLaMA [50]、Video-LLaVA [20]、LanguageBind [56] 和 Valley [25] 等。
- 不同于静态图像，视频的视觉标记往往超出 MLLM 的最大上下文容量，因此大部分方法通过采样的方法来适配输入限制，例如：Video-ChatGPT [26]，引入了更高效的视频特征表示。
面向长视频理解的 MLLMs
- 长视频理解面临更大挑战，尤其是关键帧选择的难度显著增加，容易导致关键信息严重丢失。
- 尽管一些 MLLM 采用具有更大上下文容量的语言模型，以编码和处理更多帧，但更多方法则设计了特定策略来缓解该问题，例如：
  - MovieChat [34] 引入了短期和长期记忆库来压缩并保留视频内容；
  - MA-LMM [11] 和 VideoStreaming [30] 使用Q-former和小型语言模型（phi-2 [12]）来压缩视频数据；
  - LongVLM [42] 采用标记合并（token merging）技术以减少视频标记数量；
  - Goldfish [2] 将短视频理解与信息检索相结合，以回答复杂查询。
- 局限：这些方法旨在减少视频标记数量，但通常无法保证视频中的关键信息得以保留。

3 方法

3.1 预备知识

视频理解的定义：

输入：一段视频片段 V \in \mathbb{R}^{(T×W×H×C)} 和一条文本指令 \mathbf{Q}
输出：一个文本答案
处理流程：
- 视每一帧为一张图像 \mathbf{V}_t(t \in \{1, 2, ..., T\})，提取视觉标记 \mathbf{F}_t
- 采用一个标准的 MLLM G(\{\mathbf{F}_t\})，其处理视频理解任务的模板为：[User: ⟨video-tokens⟩ ⟨text-instruction⟩ Assistant: ]，其中视频标记和文本指令通过 MLP 投影到相同的特征空间。
- (为简化表述，这里省略语言模型部分，仅关注视觉标记作为上下文的作用)
困难：在处理长视频时面临困难。

本文目标，设计一个选择函数 KS_M(\mathbf{Q}, \mathbf{F})，该函数输出一个索引集合 \mathcal{I} ⊆ \{1, 2, ..., T\}，且 |\mathcal{I}| = M ，表示选出的 M 个最优关键帧（M 根据 MLLM 的上下文容量预先设定）。从这些关键帧中提取的视频标记（即 \{\mathbf{F}_t | t \in KS_M(\mathbf{Q}, \mathbf{F})\} ）构成 MLLM 的上下文。

本文方法的整体框架如图2所示。

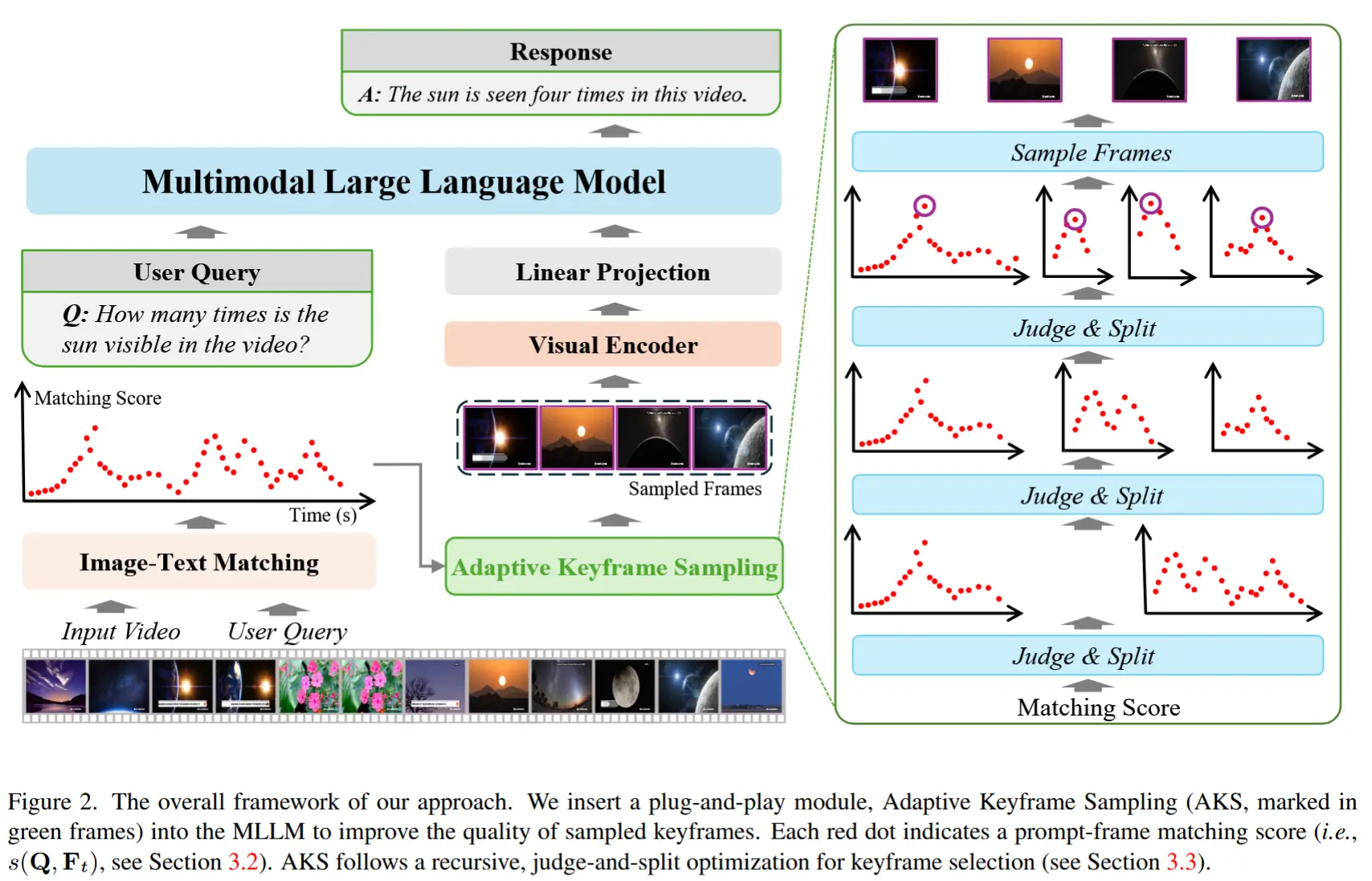
3.2. 关键帧选择的原则

关键帧选择函数 \text{KS}_M(\mathbf{Q}, \mathbf{F}) 的目标是最大化有用信息的总量，即：

\text{KS}_M(\mathbf{Q}, \mathbf{F}) = \arg\max_{|\mathcal{I}|=M} G'(\{\mathbf{F}_t \mid t \in \mathcal{I}\}). \quad (1)

这里，假设 G'(\cdot) 是 G(\cdot) 的互补函数，表示 MLLM 对其输出的置信度。公式 (1) 在数学上难以求解，原因有两个：（1）优化问题涉及指数级数量的候选集合 \mathcal{I} ；（2）函数 G'(\cdot) 难以估计，因为关键帧选择任务缺乏监督信号——即使存在训练集，且可以将 G(\cdot) 的输出与真实答案进行比较，也无法保证一个正确答案对应一组完美的关键帧，反之亦然。

为此，作者提出一种启发式方法来近似公式 (1)。直观上，当满足以下两个条件时，一组关键帧具有较高的信息量：

每一帧与提示之间的相关性较高，即视觉数据对回答问题有帮助；
所选帧在时间上的覆盖度足够，能够全面回答问题。

需要注意的是，覆盖度难以量化，但是条件二与防止冗余帧被选中密切相关，因为在关键帧总数固定的情况下，选择过多相似帧会减少其他有用信息的容量，从而损害整个关键帧集合的时间覆盖能力。

基于上述分析，重新表述公式 (1) 的右侧，得到：

\text{KS}_M(\mathbf{Q}, \mathbf{F}) = \arg\max_{|\mathcal{I}|=M} \sum_{t \in \mathcal{I}} s(\mathbf{Q}, \mathbf{F}_t) + \lambda \cdot c(\mathcal{I}). \quad (2)

其中，我们引入两个量：

s(\mathbf{Q}, \mathbf{F}_t) 表示提示 \mathbf{Q} 与第 t 帧 \mathbf{F}_t 之间的相关性；
c(\mathcal{I}) 表示整个关键帧集合在时间轴上的覆盖度；
\lambda 是用于平衡的超参数。

计算 s(\mathbf{Q}, \mathbf{F}_t) 。

这需要一个视觉-语言（VL）模块来衡量帧 \mathbf{F}_t 是否包含回答问题 \mathbf{Q} 所需的信息（MLLM 自己可以承担这一角色，但计算成本太高）。在实际应用中，选择使用更轻量级的 VL 模型（例如 CLIP 或 BLIP ITM ）。

估计 c(\mathcal{I}) 。

衡量覆盖度是一个开放性问题，与数据分布的均匀性密切相关。在数学中，Ripley 的 K -函数 [33] 是一种常用的度量均匀性的方法。给定时间戳集合 \mathcal{I} 和任意搜索半径 r < T ， r 的 K -函数记为 \hat{K}(r) ，其值与满足 |t_i - t_j| < r 的帧对 (t_i, t_j) 的数量成正比。若 \hat{K}(r) 近似与 r^2 成正比，则认为时间分布是均匀的（即覆盖了整个时间轴）。

为了将 K -函数应用于覆盖度计算（该任务与均匀性密切相关但略有不同），并降低计算开销，作者引入宽度为 r 的分桶，并将指示函数 \mathbb{I}(|t_i - t_j| < r) 近似为判断 t_i 和 t_j 是否落在同一桶中。采用递归划分策略：

在第一层，设置两个宽度为 T/2 的桶，即将时间轴 [0, T) 划分为两个不重叠区间：[0, T/2) 和 [T/2, T)。设这两个区间中的关键帧数量分别为 m_1 和 m_2 ，则覆盖度惩罚项为 |m_1 - m_2| ，因为分布不均意味着某些时间段的关键帧较少，覆盖较弱。
在第二层，每个子区间进一步划分为两个子桶，继续相同计算。
递归过程持续到第 L 层，其中 L \leq \lceil \log_2 M \rceil 为超参数。

3.3. 自适应关键帧采样

由于覆盖度函数 c(\mathcal{I}) 的定义较为复杂，难以对公式 (2) 进行闭式或精确优化。本节讨论一种近似求解方法。与仅依赖于相关性得分 s(\mathbf{Q}, \mathbf{F}_t) 的基线方法相比，称此类考虑时间戳信息以提升关键帧选择质量的方法为“时间戳感知优化”。

首先讨论两个特殊情况：
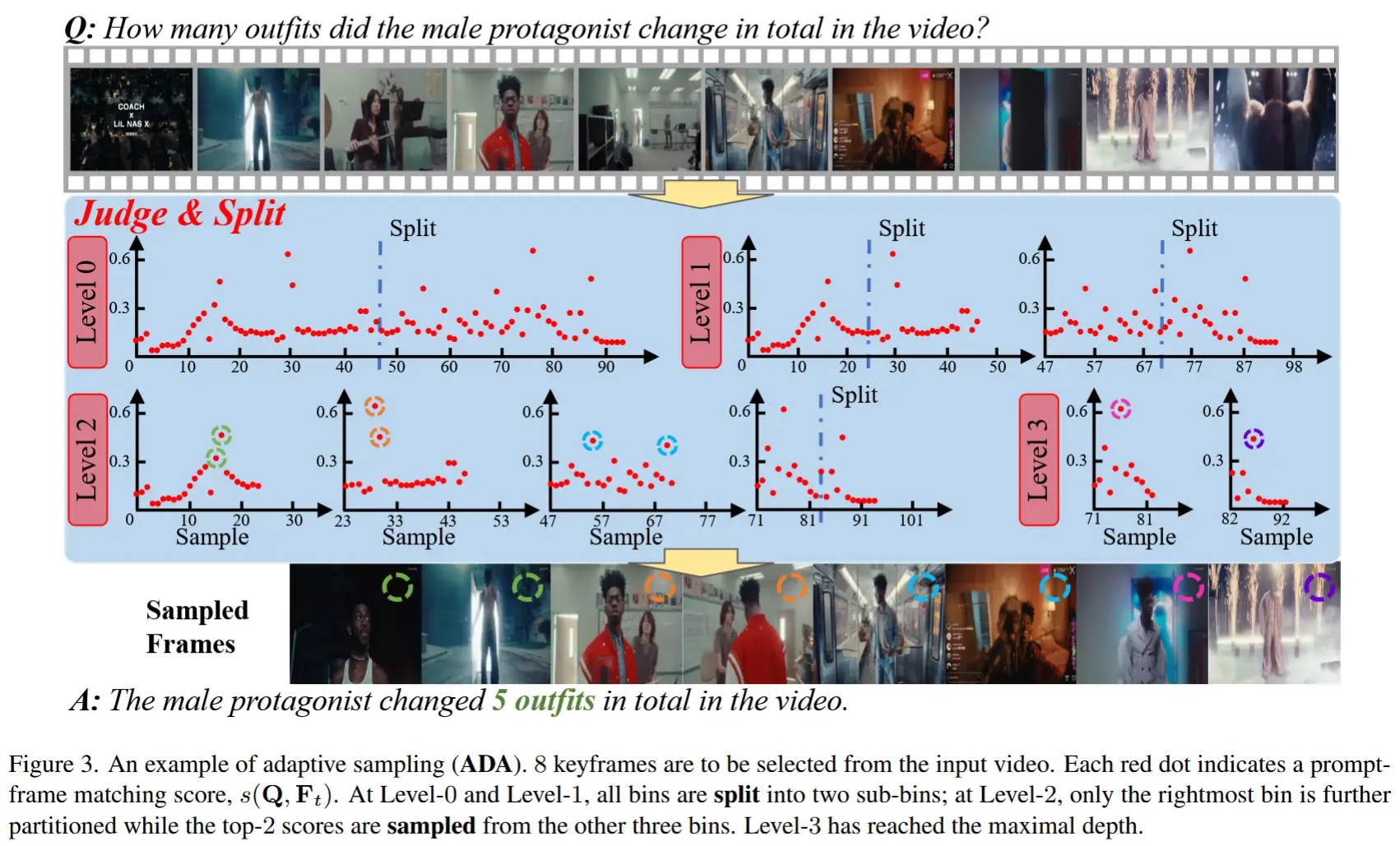
(1) 当 \lambda = 0 （即忽略覆盖度）时，公式 (2) 可通过简单选取得分最高的前 M 帧来求解。将此策略命名为 TOP，意为“顶部采样”；如图 5 所示，在某些情况下，该方法会导致所有关键帧集中在短时间内，从而使 MLLM 在其他时刻丢失重要信息。
(2) 当 \lambda \to +\infty （即严格保证覆盖度）时，公式 (2) 的解是：在每个分桶中选择得分最高的帧作为关键帧（当分桶数量超过 M 时，保留得分最高的若干帧）。我们称该策略为 BIN，简称“分桶采样”。若使用一个恒定得分的虚拟视觉-语言模型（即 s(\mathbf{Q}, \mathbf{F}_t) 对所有 t 都相同），则该策略退化为均匀采样基线，作者将其命名为 UNI，即“均匀采样”。

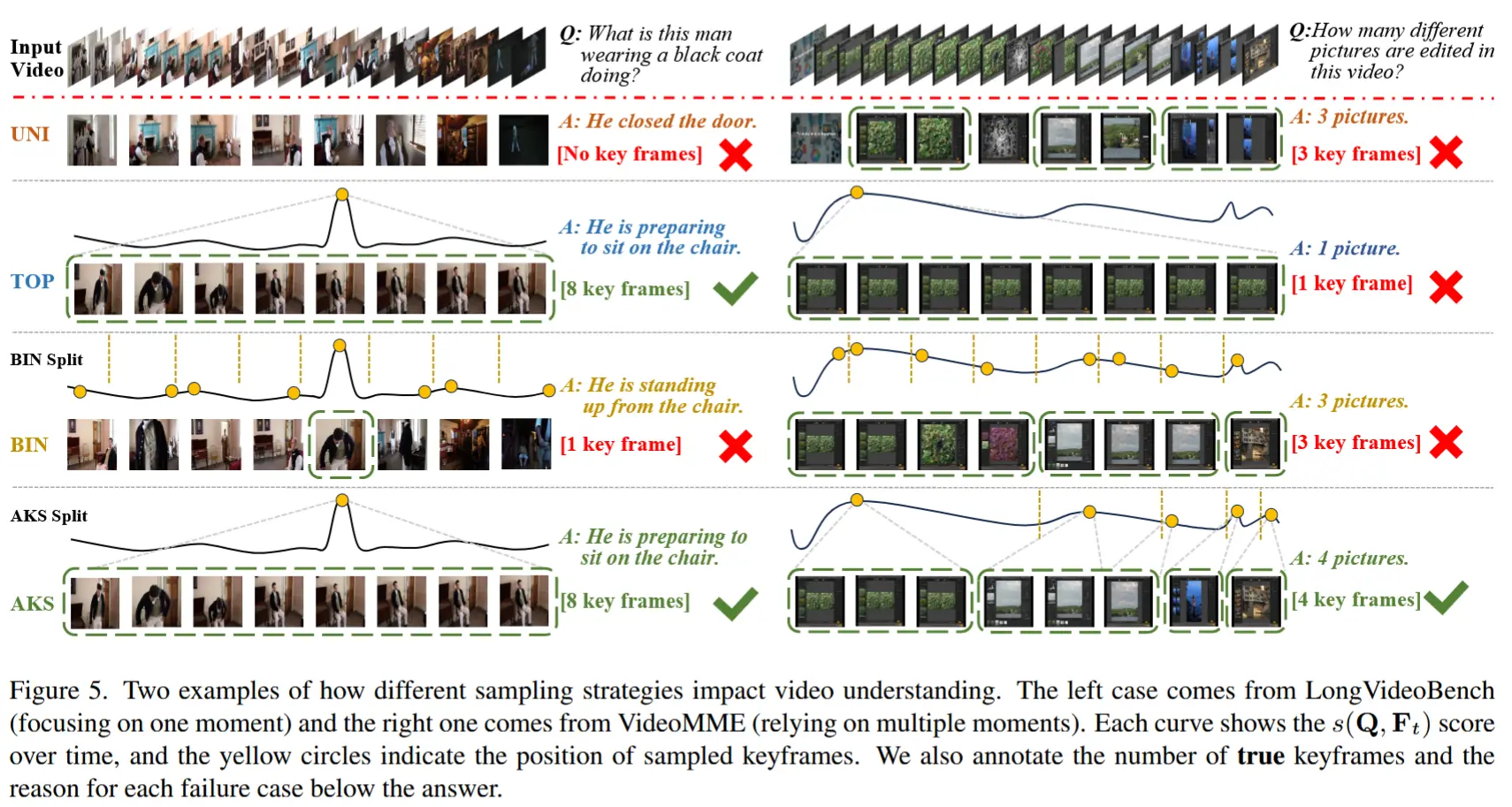
在其他情况（ 0 < \lambda \ll +\infty ）下，采用一种层次化的优化方法，遵循 c(\mathcal{I}) 的定义。在第一层，需要决定如何将 M 个关键帧分配到两个时间区间 [0, T/2) 和 [T/2, T) 中。回顾所有帧的相关性得分 s(\mathbf{Q}, \mathbf{F}_t) ，计算所有帧的平均得分（记为 s_{\text{all}} ）以及得分最高的 M 帧的平均得分（记为 s_{\text{top}} ）。如果只需选择一个关键帧，或者 s_{\text{top}} - s_{\text{all}} 超过某个阈值 s_{\text{thr}} ，作者认为应优先保证高分帧被选中（即最大化公式 (2) 的第一项），因此算法直接返回得分最高的前 M 帧作为关键帧。否则，将当前区间划分为两个子区间，并将关键帧数量均等分配（即最大化公式 (2) 的第二项），然后递归调用上述程序处理子区间。作者称该策略为 ADA，简称“自适应采样”。需要注意的是，超参数 \lambda 并未显式调节，其作用由 s_{\text{thr}} 替代。

图 3 通过一个例子展示了自适应采样（ADA）的工作过程。ADA 是 TOP 和 BIN 两种极端情况之间的折衷方案。

论文笔记《Adaptive Keyframe Sampling for Long Video Understanding》