论文 - 《Towards Stable Test-Time Adaptation in Dynamic Wild World》
代码 - Github
关键词 - TTA、ICLR2023

摘要

研究背景
- 测试时自适应（TTA）的在线模型更新可能不稳定，这通常是阻碍现有 TTA 方法在实际场景中部署的关键障碍。
- 具体来说，当测试数据具有以下特性时，TTA 可能无法提升模型性能，甚至可能损害性能：
  - 1) 混合分布偏移
  - 2) 小批量大小
  - 3) 在线类别分布不平衡的偏移
准备工作
- 研究了不稳定的根源，发现 batchnorm layer 是导致 TTA 不稳定的重要因素。相反，使用与批次无关的归一化层（如 group and layer norms）可以使 TTA 更加稳定。
- 然而，即使是使用组归一化和层归一化的 TTA 也并不总是成功，仍然存在许多失败案例。通过深入分析这些失败案例，作者发现某些梯度较大的噪声测试样本可能会干扰模型的自适应过程，导致模型崩溃为平凡解。
解决办法
- 为了解决上述崩溃问题，作者提出了一种锐度感知且可靠的熵最小化方法，称为 SAR。从两个方面进一步稳定 TTA：
  - 移除部分具有较大梯度的噪声样本。
  - 鼓励模型权重趋向平坦的最小值，从而使模型对剩余的噪声样本具有鲁棒性。

1 引言

TTA 实验设置
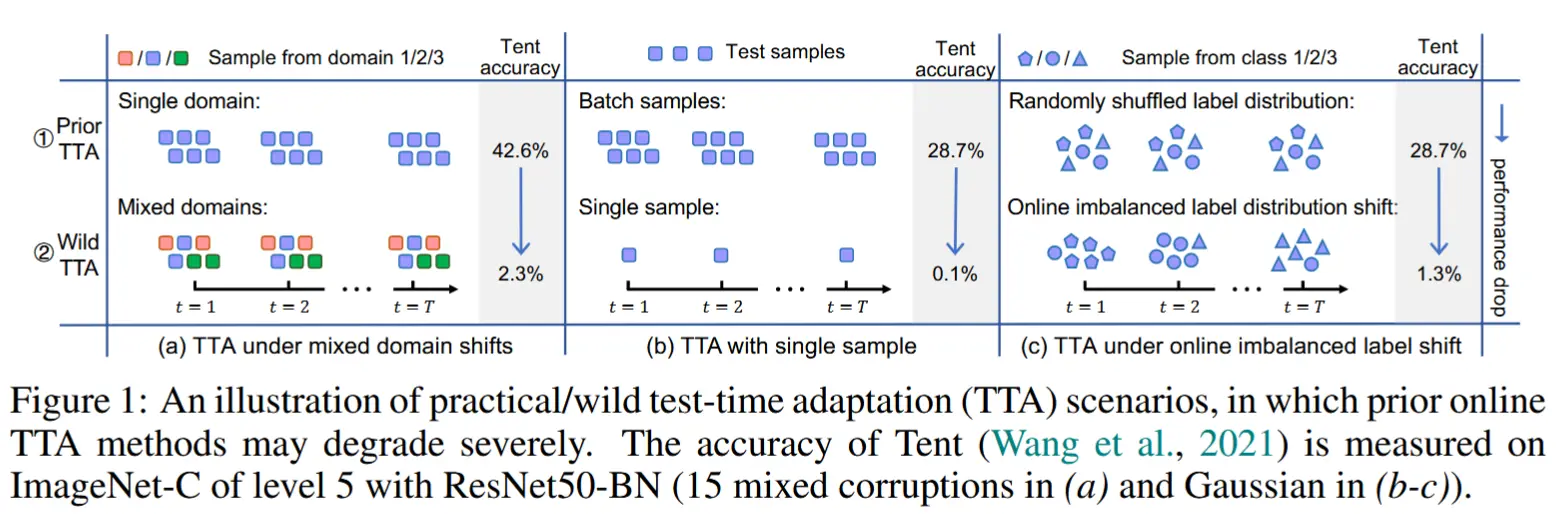
- 当前TTA的卓越性能通常是在温和的测试设置下实现的，例如使用具有相同分布偏移类型且标签分布随机打乱的一批测试样本进行自适应（如图①）。
- 在复杂的真实世界中，测试数据可能以任意方式到来。如图 1② 所示，测试场景可能会遇到以下情况：
  - i) 多种分布偏移的混合。
  - ii) 较小的测试批次大小（甚至单个样本）。
  - iii) 真实测试标签分布 Q_t(y) 在线偏移，并且 Q_t(y) 在每个时间步 t 可能是不平衡的。
- 在这些复杂的测试设置下，使用现有的 TTA 方法在线更新模型可能是不稳定的，即无法帮助甚至可能损害模型的鲁棒性。

前人工作
- 为了稳定复杂的 TTA，一个直接的解决方案是在每次对样本或小批量进行自适应后恢复模型权重，例如 MEMO（Zhang et al., 2022）和 episodic Tent（Wang et al., 2021）。
- 同时，DDA（Gao et al., 2022）提供了一种潜在有效的思路来解决这一问题：与其进行模型自适应，它试图将测试样本转移到源训练分布（通过训练好的扩散模型），在测试过程中所有模型权重均被冻结。
- 局限：这些方法无法累积利用先前测试样本的知识来提升自适应性能，因此在测试样本数量较多时效果有限。此外，DDA 中的扩散模型需要具备良好的泛化能力，并能够将任何可能的目标偏移投影到源数据上，这一点很难完全满足。

本文工作
- 作者首先指出，批归一化（BN）层 是一个关键障碍，因为在上述复杂的场景下，BN 层中的均值和方差估计会存在偏差。并发现使用与批次无关的归一化层（ GN 和 LN ）的预训练模型对稳定的 TTA 更加有利。
- 然而，在 GN/LN 模型上的 TTA 通过在线熵最小化优化的 GN/LN 模型（Wang et al., 2021）容易发生 模型崩溃 ，尤其是在分布偏移较为严重的情况下。
- 为此，作者提出了一种锐度感知且可靠的熵最小化方法 （称为 SAR）。
  - 根据样本的熵值过滤掉部分具有较大且噪声较多梯度的样本，使其不参与自适应。
  - 对于剩余的样本，我们引入了一种锐度感知的学习方案，以确保模型权重被优化到平坦的最小值，从而对较大的噪声梯度/更新具有鲁棒性。

2 通过测试熵和锐化最小化实现稳定适应

2.1 不稳定TTA原因

本节首先通过分析 TTA 中归一化层的影响来研究为什么在复杂场景下 TTA 会失败，并深入探讨基于熵的方法（如组归一化）不稳定的原因。

批归一化

在 TTA 中，先前的方法通常对带有批归一化（BN）层的预训练模型进行自适应，并且大多数方法都是基于 BN 统计的自适应。具体来说，对于输入维度为 d 的层 \mathbf{x} = (x^{(1)}, \dots, x^{(d)})，经过批归一化的输出为：

y^{(k)} = \gamma^{(k)} \widehat{x}^{(k)} + \beta^{(k)},

其中，\widehat{x}^{(k)} = \frac{x^{(k)} - \mathbb{E}[x^{(k)}]}{\sqrt{\text{Var}[x^{(k)}]}}。这里，\gamma^{(k)} 和 \beta^{(k)} 是可学习的仿射参数。

BN 自适应方法通过对（小批量）测试样本计算均值 \mathbb{E}[x^{(k)}] 和方差 \text{Var}[x^{(k)}] 来更新统计量。 然而，在复杂的 TTA 场景中，所有可能导致 TTA 失败的三种实际自适应设置都会导致均值和方差估计出现问题：

多分布共享统计量的问题：在复杂 TTA 场景中，BN 统计实际上代表了多个分布，理想情况下每个分布应该有自己的统计量。简单地从小批量测试样本中估计多个分布的共享 BN 统计量不可避免地会导致性能有限，例如在多任务/多领域学习中。
批次大小对统计质量的影响：估计统计量的质量依赖于批次大小，使用非常少的样本（即小批量）很难准确估计统计量。
类别不平衡导致的偏差：类别不平衡也会导致某些特定类别的 BN 统计量出现偏差。

作者给出的这三个原因非常有说服力！总而言之就是，更加复杂的场景导致估计统计量难以准确得到，因此BN失效。

（结论） 基于以上分析可知，与批次无关的归一化层（即对样本如何分组到批次中无感知的层），如GN和LN，更适合用于 TTA。

在线熵最小化

（核心思想）尽管 TTA 在 GN 和 LN 模型上表现得更加稳定，但它并不总是成功，并且仍然面临多个失败案例（如第 4 节所示）。

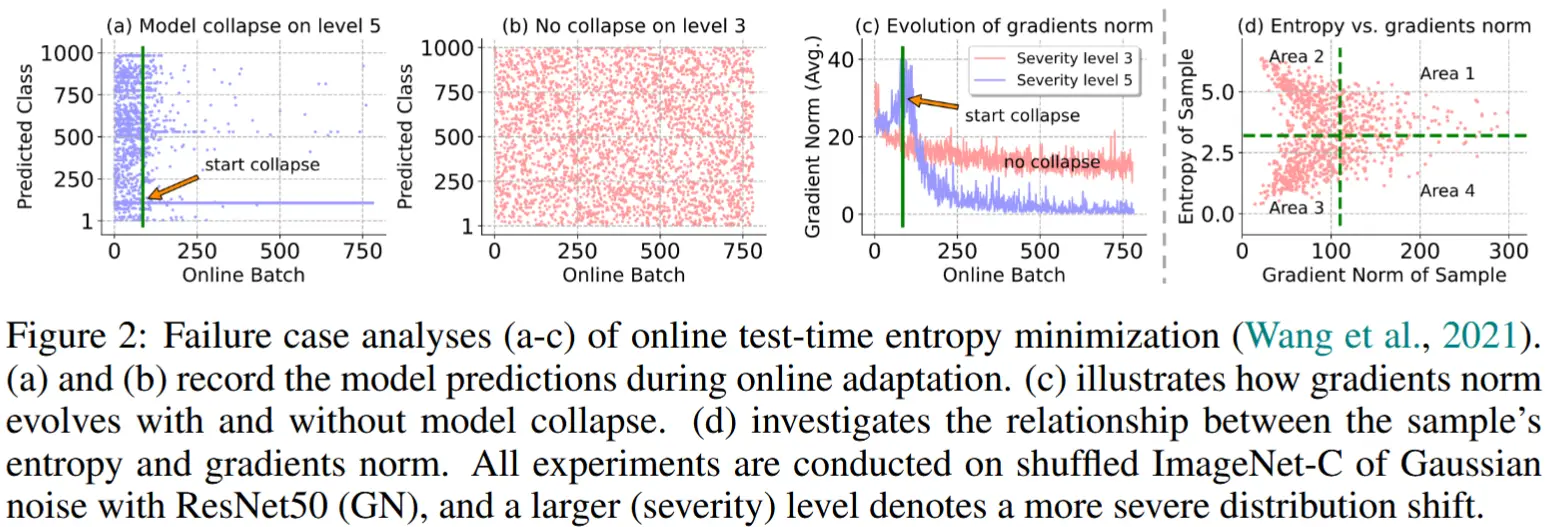
（实验验证） 在在线自适应过程中，作者记录了 ResNet50-GN 在高斯噪声下的 ImageNet-C 数据集（经过打乱处理）的预测类别以及由熵损失产生的梯度范数。通过比较图 2(a) 和 (b)，可以看出熵最小化是不稳定的，并且在分布偏移严重时容易出现崩溃（图 2(a)）。与此同时，我们注意到，当模型开始崩溃时，所有可训练参数的 \ell_2 -范数突然增加，然后迅速下降到接近 0（图 2(c)），而在严重程度 3 的情况下，模型表现良好，梯度范数始终保持在一个稳定的范围内。

（结论）这表明某些测试样本会产生较大的梯度，可能会损害自适应过程并导致模型崩溃。

2.2 锐度感知且可靠的测试时熵最小化

两种最直接解决方案是根据样本梯度 过滤测试样本 或 执行梯度裁剪。然而，这些方法并不实用，因为不同模型和分布偏移类型下的梯度范数具有不同的尺度，因此很难设计一种通用的方法来设置样本过滤或梯度裁剪的阈值。作者提出以下解决方案。

可靠的熵最小化

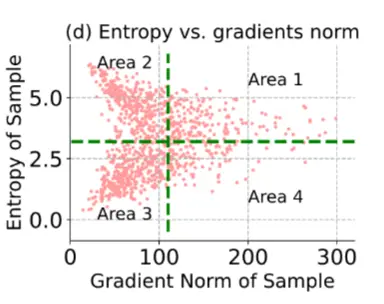
由于直接根据梯度范数过滤样本不可行，作者首先研究了熵损失与梯度范数之间的关系，并试图基于熵去除具有大梯度的样本。在这里，熵依赖于模型的输出类别数 C ，并且对于不同的模型和数据，熵属于区间 (0, \ln C)。从这个意义上讲，根据熵进行样本过滤的阈值更容易选择。如图 2(d) 所示，选择小损失值的样本可以将部分具有大梯度的样本（ area@1）排除在自适应之外。形式上，令 E(\mathbf{x}; \Theta) 表示样本 \mathbf{x} 的熵，则选择性熵最小化定义为：

\min_{\Theta} S(\mathbf{x}) E(\mathbf{x}; \Theta), \quad \text{wher } S(\mathbf{x}) \triangleq \mathbb{I}_{\{E(\mathbf{x}; \Theta) < E_0\}}(\mathbf{x}), \tag{2}

这里，\Theta 表示模型参数，\mathbb{I}_{\{\cdot\}}(\cdot) 是指示函数，E_0 是预定义的参数。需要注意的是，上述标准还会移除图 2(d) 中的 area@2 内的样本，这些样本置信度较低，因此不可靠。

锐度感知的熵最小化

理想情况下，我们希望仅通过 area@3 中的样本来优化模型，因为 area@4 中的样本仍然具有较大的梯度，可能会对自适应过程造成损害。然而，通过过滤方案进一步移除 area@4 中的样本是困难的。因此，我们转而寻求使模型对 area@4 中样本所贡献的大梯度不敏感。

为此，作者鼓励模型进入熵损失曲面的平坦区域。原因在于，平坦的极小值具有良好的泛化能力，并且对噪声或大梯度具有鲁棒性，即在平坦极小值上的噪声或大更新不会显著影响原始模型的损失，而尖锐的极小值则会受到影响。为此，通过以下方式共同最小化熵和熵损失的尖锐度：

\min_{\Theta} E^{SA}(\mathbf{x}; \Theta), \quad \text{where } \quad E^{SA}(\mathbf{x}; \Theta) \triangleq \max_{\|\epsilon\|_2 \leq \rho} E(\mathbf{x}; \Theta + \epsilon). \tag{3}

这里，内部优化的目标是寻找一个权重扰动 \epsilon，使得在以半径为 \rho 的欧几里得球内，熵达到最大值。锐度通过 \Theta 和 \Theta + \epsilon 之间的熵的最大变化来量化。这种双层优化问题鼓励优化过程找到平坦的极小值。为了处理公式 (3)，我们遵循 SAM 的方法，首先通过一阶泰勒展开近似求解内部优化问题，即：

\epsilon^*(\Theta) \triangleq \arg\max_{\|\epsilon\|_2 \leq \rho} E(\mathbf{x}; \Theta + \epsilon) \\ \approx \arg\max_{\|\epsilon\|_2 \leq \rho} E(\mathbf{x}; \Theta) + \epsilon^T \nabla_\Theta E(\mathbf{x}; \Theta) \\ = \arg\max_{\|\epsilon\|_2 \leq \rho} \epsilon^T \nabla_\Theta E(\mathbf{x}; \Theta).

然后，解决这一近似的 \hat{\epsilon}(\Theta) 是经典对偶范数问题的解：

\hat{\epsilon}(\Theta) = \rho \cdot \frac{\text{sign}(\nabla_\Theta E(\mathbf{x}; \Theta)) \cdot |\nabla_\Theta E(\mathbf{x}; \Theta)|}{\|\nabla_\Theta E(\mathbf{x}; \Theta)\|_2}. \tag{4}

将 \hat{\epsilon}(\Theta) 代入公式 (3) 并进行微分，忽略二阶项以加速计算，最终的梯度近似为：

\nabla_\Theta E^{SA}(\mathbf{x}; \Theta) \approx \nabla_\Theta E(\mathbf{x}; \Theta) \big|_{\Theta + \hat{\epsilon}(\Theta)}. \tag{5}

总体优化

综上所述，我们的锐度感知且可靠的熵最小化方法为：

\min_{\tilde{\Theta}} S(\mathbf{x}) E^{SA}(\mathbf{x}; \Theta), \tag{6}

其中，S(\mathbf{x}) 和 E^{SA}(\mathbf{x}; \Theta) 分别在公式 (2) 和 (3) 中定义，\tilde{\Theta} \subset \Theta 表示测试时自适应过程中可学习的参数。此外，为了避免公式 (6) 在少数极端困难情况下失效，进一步引入了一种模型恢复方案。记录熵损失值的移动平均值 e_m，一旦 e_m 小于一个小阈值 e_0，就将 \tilde{\Theta} 重置为原始值，因为模型崩溃后会产生非常小的熵损失。在这里，额外的内存开销可以忽略不计，因为仅优化归一化层中的仿射参数。

3 实证研究归一化层

3.1 实验设计

模型：ResNet-50-BN、ResNet-50-GN、VitBase-LN
代表性方法：自监督Test-Time Training、无监督Tent

3.2 研究结果

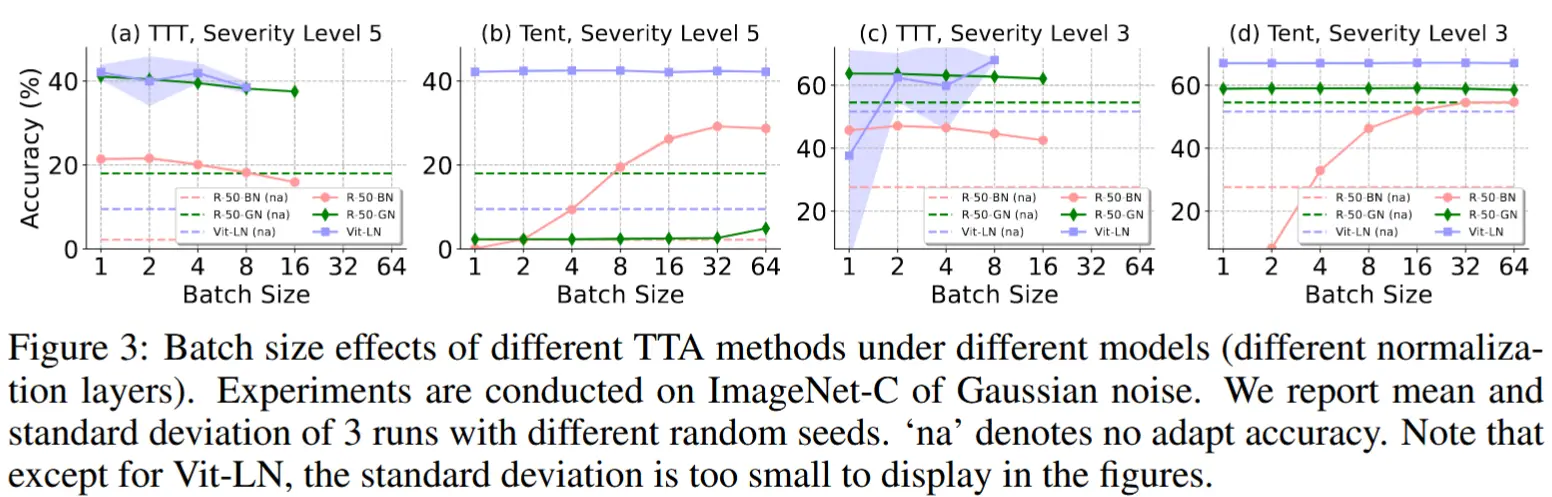
小测试批次下 TTA 中的Norm Layer影响
- 实验方法：评估不同批量大小（1, 2, 4, 8, 16, 32, 64）下，TTA方法（TTT和Tent）的效果。由于GPU内存限制，TTT的批量大小仅报告到8或16。
- 如图3所示，可以得到以下结论
  - Tent方法在小批量情况下，R-50-GN和Vit-LN比R-50-BN更不容易受批量大小变化的影响，但仍然存在失败案例。
  - TTT方法对于不同批量大小的适应性较强，但在Vit-LN上表现出不稳定性，尤其是对样本顺序的高度敏感性。
  - R-50-BN的表现最为稳定，尤其是在批量大小为1时，得益于增强技术对单一样本的处理。

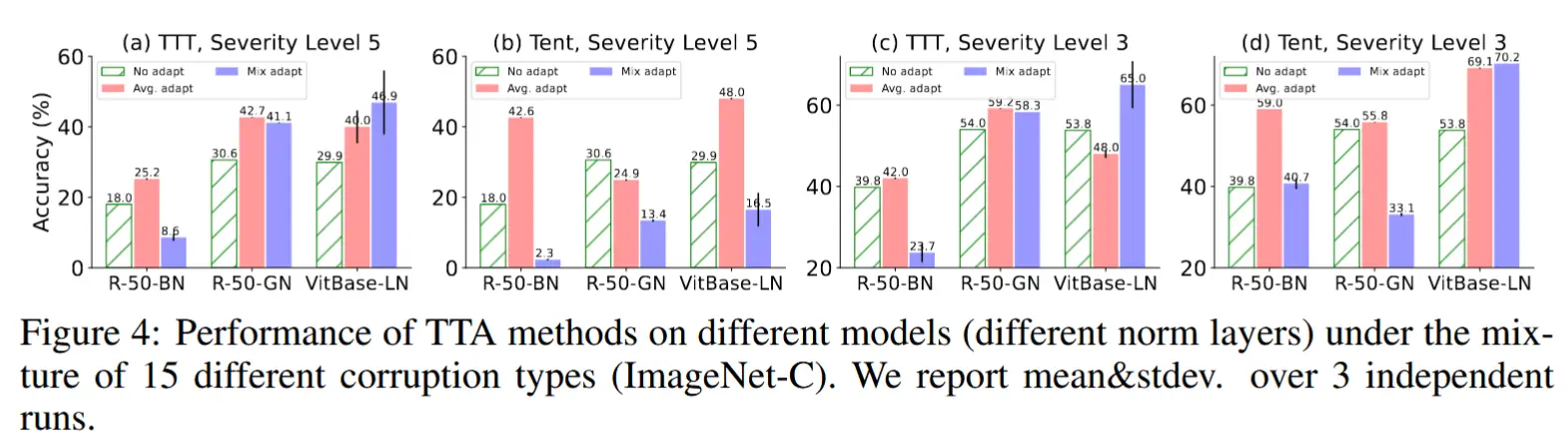
混合分布偏移下 TTA 中的Norm Layer影响
- 实验方法：评估Tent和TTA在不同归一化层模型熵，在在测试数据来自多个分布发生变化的域时的表现。同时设计了三种情景：No Adapt、Avg. adapt（分别对每个域进行自适应的平均准确率）、Mix adapt（在多个混合的、发生变化的域上进行自适应的准确率）
- 如图4所示，可以得到以下结论
  - R-50-GN和Vit-LN在面对混合分布变化时比R-50-BN更稳定，能够保持较好的适应性。
  - TTT方法在R-50-GN和Vit-LN上的表现普遍更稳定，尤其是在混合域适应（mix adapt）任务中。
  - Tent方法在某些情况下（尤其是在R-50-GN和Vit-LN的特定层级上）表现较差，失败的案例更多。
  - TTT+Vit-LN表现出对样本顺序的较大敏感性，表明其在多个运行中的方差较大。

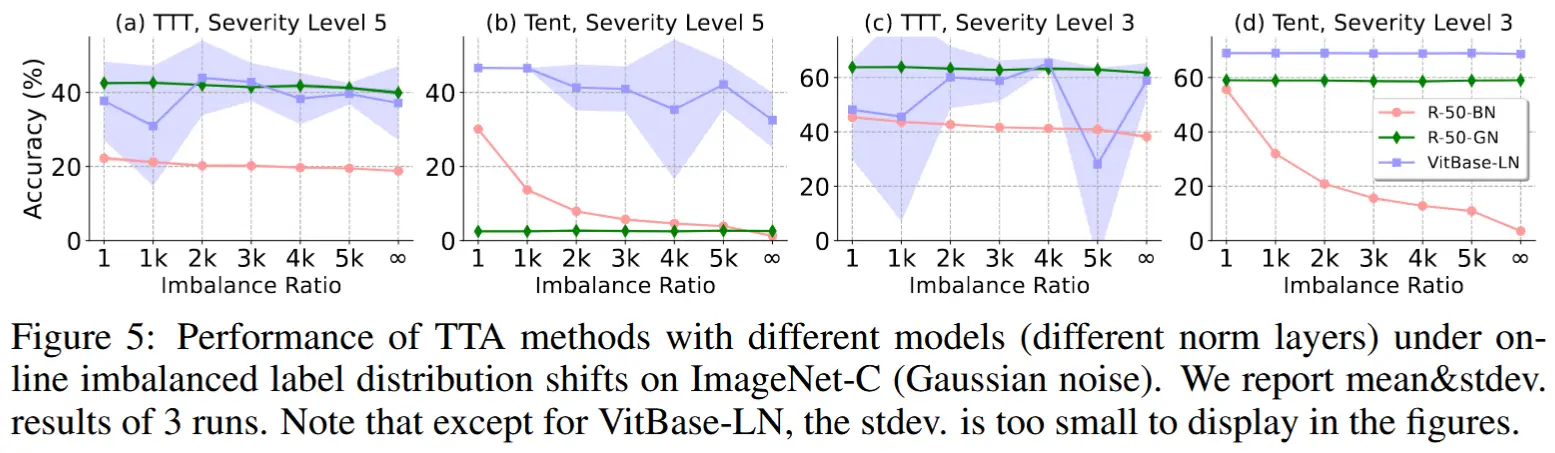
在线不平衡标签偏移下 TTA 中的Norm Layer影响
- 实验方法：假设有 T 个时间步长，并且 T 等于类别数 C。设置概率向量 Q_t(y) = [q_1,q_2, ..., q_C ]，其中 q_c = q_{max}，if \ c = t，且 q_c = q_{min} = (1 − q_{max})/(C − 1), if \ c \neq t。这里，q_{max}/q_{min} 表示不平衡比。然后，在每 t \in \{1, 2, ..., T=C\}，我们根据 Q_t(y) 从测试集中采样 M 张图像。
- 如图5所示，可以得到以下结论
  - R-50-GN和Vit-LN在面对在线不平衡标签分布变化时表现出较好的稳定性，尤其在高不平衡比例下，能够保持较好的适应性。
  - R-50-BN在不平衡标签分布变化下的适应性较差，尤其是在不平衡比例较大时，表现显著下降。
  - Tent方法在不平衡标签分布变化时表现出较大的敏感性，尤其是在使用R-50-GN时，存在较严重的失败情况。
  - TTT方法的表现较为稳定，但TTT+Vit-LN在多次实验中的方差较大，表明对样本顺序的敏感性较高。

4 实验

4.1 实验设定

数据集：ImageNet-C
基线：DDA\MEMO\Tent\EATA
模型：ResNet50-BN/GN和VitBase-LN

4.2 WILD 测试设置下鲁棒性

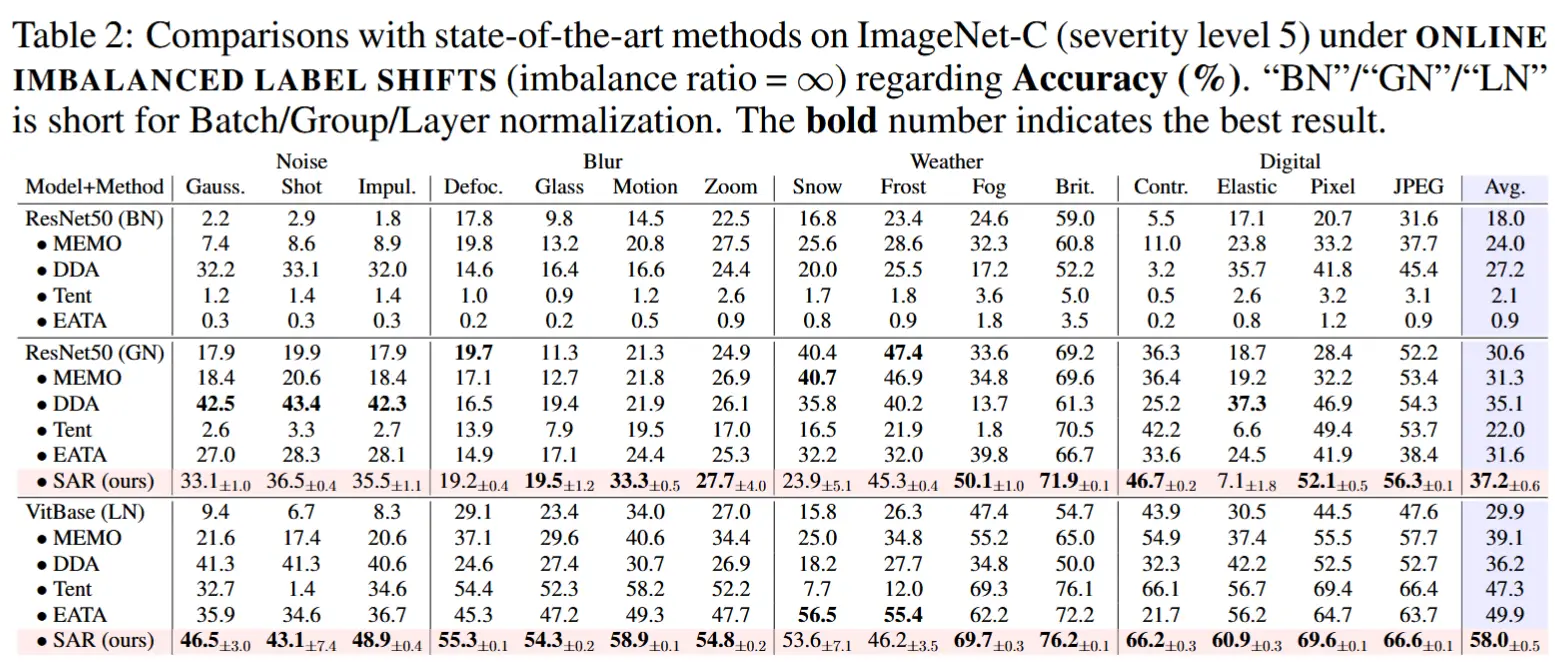
在线不平衡标签分布变化下
- 设置不平衡比为无穷。
- 结果如表2所示，可以得到以下结论
  - SAR方法在面对在线不平衡标签分布变化时表现优异，在不同腐蚀类型下均能取得最佳结果。
  - Tent方法在一些腐蚀类型上表现较好（如焦点模糊和运动模糊），但在ResNet50-BN上总是失败，且在部分特定腐蚀类型上失败更多。
  - EATA方法相比Tent在失败案例上有所减少，并能通过权重正则化缓解一些模型崩溃问题。

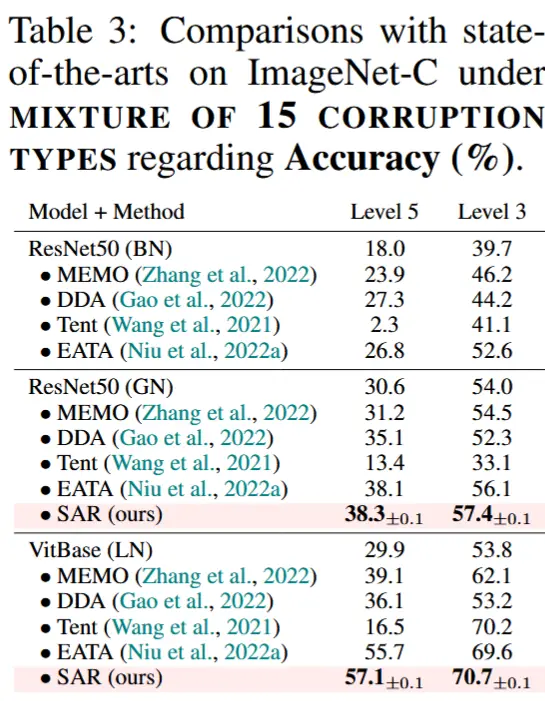
混合分布变化下
- 对15种腐蚀类型的混合数据集进行评估，包含50,000张图像，分为不同的严重程度级别（5和3）
- 结果如表3所示，可以得到以下结论
  - SAR在面对混合分布变化时持续表现优异，准确率优于所有对比方法。
  - MEMO和DDA在准确率上优于Tent，但由于计算开销较大，且DDA需要修改训练过程，因此效率较低。
  - EATA方法在准确率上也有较好表现，但需要额外的分布内测试样本，这可能会带来实际应用上的不便。

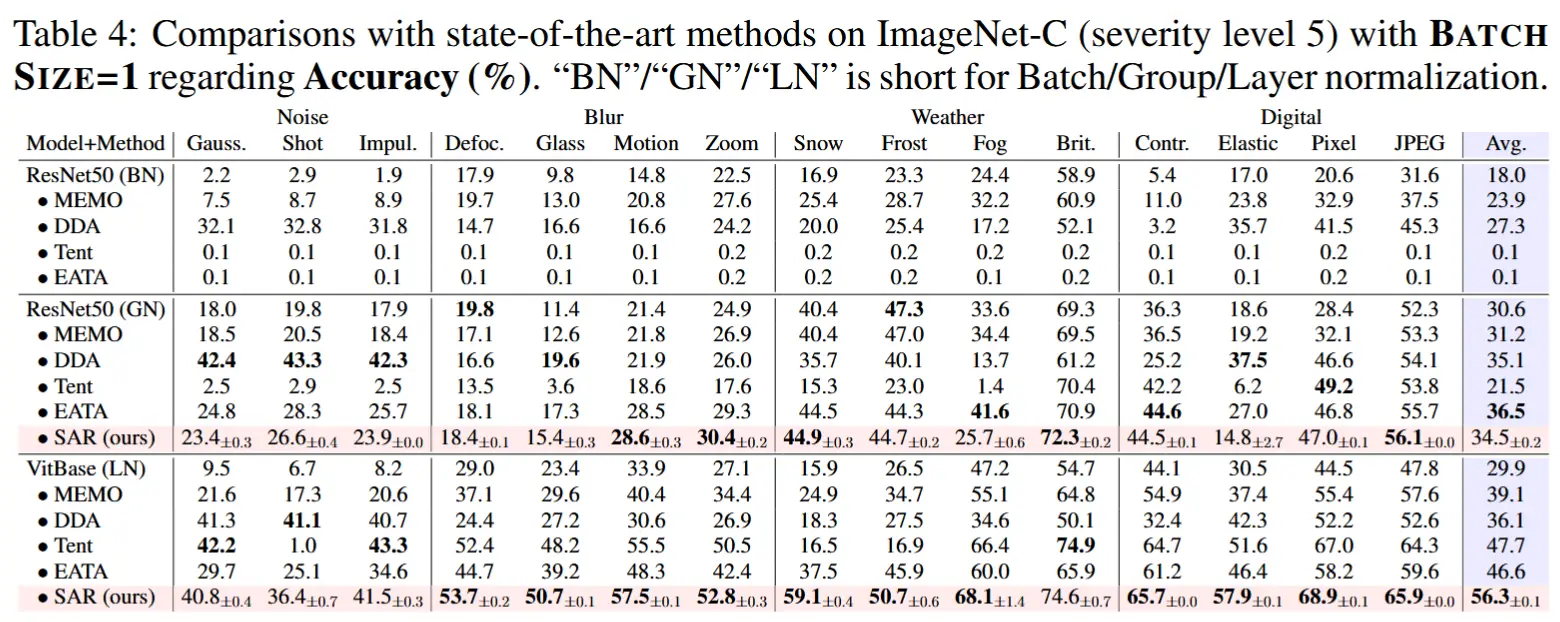
批量大小为1
- 实验在批量大小为1（即每次只有一个样本）时进行比较
- 结果如表4所示，可以得到以下结论
  - SAR在批量大小为1时表现出色，取得了最佳结果。
  - MEMO和DDA虽然不受小批量或其他变化的影响，但由于计算复杂度高，且无法充分利用先前图像的信息，性能提升有限。

论文笔记《Towards Stable Test-Time Adaptation in Dynamic Wild World》

摘要