论文笔记《Feature Augmentation based Test-Time Adaptation》

论文笔记《Feature Augmentation based Test-Time Adaptation》

Administrator 22 2025-04-25
  • 论文 - 《Feature Augmentation based Test-Time Adaptation》
  • 代码 - Github
  • 关键词 - WACV、TTA、特征增强、熵最小化

摘要

  • 研究背景
    • 测试时适应（TTA）允许模型在无法访问源数据的情况下适应未见过的领域。由于实际环境的特性，TTA用于适应的数据量有限。
    • 最近的TTA方法通过过滤输入数据以提高可靠性，进一步限制了数据量，使得有效数据规模更小，从而限制了适应潜力。
  • 本文工作
    • 提出了 基于特征增强的测试时适应方法（FATA），这是一种充分利用有限输入数据的简单方法。
    • FATA采用 归一化扰动 来增强特征，并通过 FATA损失函数 使 增强特征与原始特征的输出 保持相似，从而实现模型的适应。
    • FATA是与模型无关的方法，可以无缝集成到现有模型中，而无需更改模型架构。

1 相关工作

1.1 TTA

略


1.2 特征增强

  • 数据增强
    • 在领域泛化领域，数据增强已被证明是一种充分利用源数据的有效方法。
    • 现有的数据增强方法依赖于图像空间的操作，这些方法需要精心设计增强策略，并消耗大量的计算资源。
  • 特征增强
    • 最近，特征增强被提出作为解决数据增强中有限多样性和效率不足的一种解决方案。
    • 通过在特征空间中应用变换 [14]，以模拟训练过程中各种特征分布 [29]，特征增强比传统数据增强方法更有效地提升模型对新领域的泛化能力。
  • 特征增强相关工作
    • MixStyle [38] 提出了一种显式的增强方法，通过插值利用领域标签扰动潜在特征。
    • Li 等人 (2021) [14] 提出了随机特征增强（Stochastic Feature Augmentation, SFA），该方法通过对从正态分布中随机采样的权重和偏置使用线性函数来增强潜在特征。SFA 可以作为一个即插即用的模块实现，使其能够灵活集成到各种模型中。
    • Fan 等人 (2023) [5] 提出了归一化扰动（Normalization Perturbation, NP），这一方法受到自适应实例归一化（AdaIN）[10] 的启发，而 AdaIN 是一种利用特征通道统计信息进行归一化和变换的风格迁移方法。与直接扰动特征不同，NP 通过对通道统计信息进行扰动，从而有效保留特征内容。
  • 本文将特征增强技术引入TTA中，通过基于熵值进行数据采样，解决了数据稀缺的问题。

2 动机

2.1 样本选择策略

基于熵最小化，Niu 等人 [19] 提出仅使用低熵值的样本过滤掉不可靠的样本。因此，模型通过基于样本选择标准 ​ S(\mathbf{x}) 选择的样本来最小化熵：

\min_\theta S(\mathbf{x}) \operatorname{Ent}_\theta(\mathbf{x}), \quad \text{where } S(\mathbf{x}) \triangleq \mathbb{I}_{\{\mathbf{x} \in \mathcal{S}\}}, \tag{2}

其中 ​ \mathbb{I}_{\{\cdot\}}(\cdot) 是指示函数，​ \mathcal{S} 是一组选定的样本。例如，基于熵的样本选择集合为 ​ \mathcal{S}_{\text{ent}} = \{\mathbf{x} | \operatorname{Ent}_\theta(\mathbf{x}) < \tau_{\text{ent}}\} ，其中 ​ \tau_{\text{ent}} 是预定义的熵阈值。


2.2 样本选择策略分析

作者测量了这种采样策略选择了多少样本。使用在 ImageNet 上预训练的 ResNet50-BN ，并根据 EATA 和 SAR 的作者推荐的熵阈值 ​ \tau_{\text{ent}} ，从目标数据集 ​ \mathcal{D}^{\text{test}} （即 ImageNet-C ）中统计被选中的样本数量。

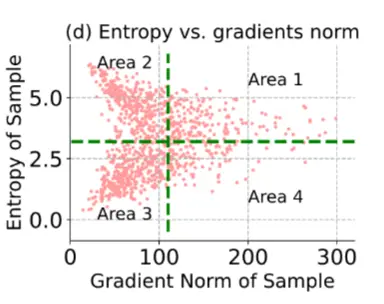
当在线目标数据量较小或存在标签不平衡时，有限的样本可能会降低适应性能。 如图 1c 所示，当使用基于熵的过滤策略时，只有 ​ 11.85\% 的 ​ \mathcal{D}^{\text{test}} 数据可以被使用。相对于数据集中的一千个类别而言，这个数量非常小。这表明平均每个类别只能使用五到六个样本进行适应（见图 1a），其中采样较少的类别的准确性较低（见图 1b），从而导致整体性能不佳。此外，DeYO 通过基于熵的过滤选择具有有益结构和形状的样本，进一步减少了使用的样本数量。

尽管样本数量有限，这些方法仍然简单地仅依赖于熵损失，而没有考虑泛化的表示。作者认为，这种方法会限制模型对目标域的暴露程度，从而导致性能提升有限。为了增强模型对目标域的暴露，并进一步利用可靠的采样数据，需要一种更复杂的方法。

paper38-1.webp

3 方法

3.1 特征增强

作者通过特征增强来充分利用有限的数据，这允许生成多样化的增强特征，如图 2 所示。给定一个由 ​ N 层组成的编码器 ​ f = f^1, f^2, \dots, f^N 和一个样本 ​ \mathbf{x} \in \mathbb{R}^{B \times C \times H \times W} ，特征增强会增强第 ​ i 层的中间特征 ​ \mathbf{z} = f^i \circ f^{i-1} \circ \dots \circ f^1(\mathbf{x}) 。例如，归一化扰动增强（NP+）使用归一化方法对中间特征 ​ \mathbf{z} \in \mathbb{R}^{B \times C_i \times H_i \times W_i} 的通道统计进行扰动，公式如下：

\mathbf{z}' = \alpha \mathbf{z} + \delta (\beta - \alpha) \mu_c, \tag{3}

其中 ​ \alpha, \beta \in \mathbb{R}^{B \times C} 是从 ​ N(\mathbf{I}, \sigma_n \mathbf{I}) 中采样的随机噪声，​ \delta = \text{Var}(\mu_c) / \max(\text{Var}(\mu_c)) 是归一化方差，​ \mu_c = \{\mu_c^j\}_{j=1}^B \in \mathbb{R}^{1 \times C_i} 是通道维度上的特征均值。

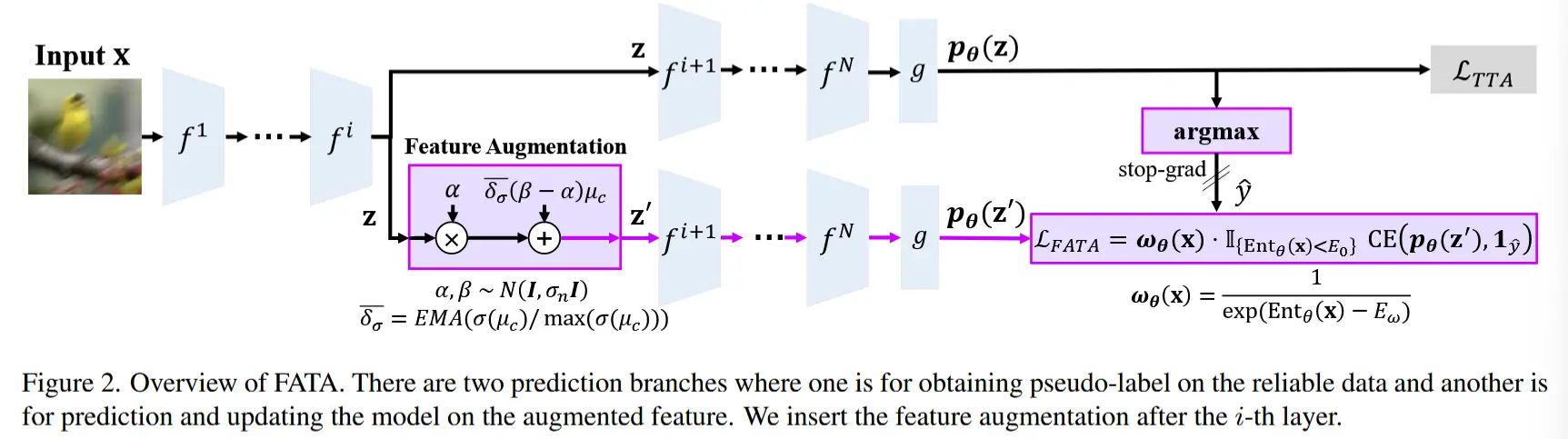
paper38-2.webp

FATA 增强中间特征 ​ \mathbf{z} 的方式如下：

\mathbf{z}' = \alpha \mathbf{z} + \overline{\delta_\sigma} (\beta - \alpha) \mu_c, \tag{4}

其中 ​ \overline{\delta_\sigma} 是归一化标准差 ​ \delta_\sigma = \sigma(\mu_c) / \max(\sigma(\mu_c)) 的指数移动平均，​ \sigma 是标准差运算符。我们将 ​ \delta 替换为 ​ \overline{\delta_\sigma} 来解决以下问题：首先，与领域泛化不同，TTA 需要从有限的数据中适应特定的域。为了自适应地调整噪声以适应目标域，我们添加了一个估计目标域统计量的指数移动平均。其次，公式 (3) 引入了方差的平方大小，因为归一化统计方差 ​ \delta 调整每个通道的均值 ​ \mu_c 来控制随机噪声。为了解决这一问题，我们将方差替换为标准差。


3.2 FATA 损失

为了充分利用增强后的特征，我们提出了 FATA 损失（FATA Loss），这是一种应用于增强特征的增强损失。

增强损失

给定一个分类器 ​ g ，增强特征的输出概率为 ​ \mathbf{p}_\theta(\mathbf{z}) = g \circ f^N \circ f^{N-1} \circ \dots \circ f^{i+1}(\mathbf{z}) 。我们提出了一种基于交叉熵的增强损失，该损失基于增强特征的输出和原始特征的伪标签之间的差异。给定伪标签 ​ \hat{y} = \text{stopgrad}(\argmax(\mathbf{p}_\theta(\mathbf{z}))) ，我们的增强损失公式如下：

\mathcal{L}_{\text{aug}}(\mathbf{x}; \theta) = \text{CE}(\mathbf{p}_\theta(\mathbf{z}'), \mathbf{1}_{\hat{y}}), \tag{5}

与 CoTTA [34] 不同，FATA 在增强特征上更新模型，并将原始数据的预测作为伪标签。因此，模型可以在更多样化的特征上进行预测并根据这些特征进行更新。此外，伪标签是可靠的，因为数据已经通过熵阈值 ​ E_0 进行了采样。


样本选择与加权

遵循 EATA [19] 的方法，我们应用基于熵的样本选择和样本加权。给定一个熵阈值 ​ E_0 和归一化因子 ​ E_w ，样本选择标准为 ​ \{\mathbf{x} | \operatorname{Ent}_\theta(\mathbf{x}) < E_0\} ，样本加权函数 ​ \omega_\theta 定义为 ​ \omega_\theta(\mathbf{x}) = 1 / \exp(\operatorname{Ent}_\theta(\mathbf{x}) - E_w) 。


FATA 增强损失

最后，我们将样本选择和加权整合到我们的增强损失中，公式如下：

\mathcal{L}_{\text{FATA}}(\mathbf{x}; \theta) = \omega_\theta(\mathbf{x}) \cdot \mathbb{I}_{\{\operatorname{Ent}_\theta(\mathbf{x}) < E_0\}} \text{CE}(\mathbf{p}_\theta(\mathbf{z}'), \mathbf{1}_{\hat{y}}), \tag{6}

其中 ​ \text{CE}(p, q) 是交叉熵函数。


总损失

给定一个 TTA 损失 ​ \mathcal{L}_{\text{TTA}} （例如熵最小化损失），我们将 FATA 增强损失纳入 TTA 损失中。因此，总损失 ​ \mathcal{L} 表示如下：

\mathcal{L} = \mathcal{L}_{\text{TTA}} + \mathcal{L}_{\text{FATA}}, \tag{7}

该公式结合了 TTA 损失和 FATA 增强损失。所提出的损失可以无缝集成到任何方法中，而无需修改 TTA 损失（如基于样本选择的熵最小化损失）。

TTA 论文笔记