论文笔记《CAFA: Class-Aware Feature Alignment for Test-Time Adaptation》

论文笔记《CAFA: Class-Aware Feature Alignment for Test-Time Adaptation》

Administrator 20 2025-04-28
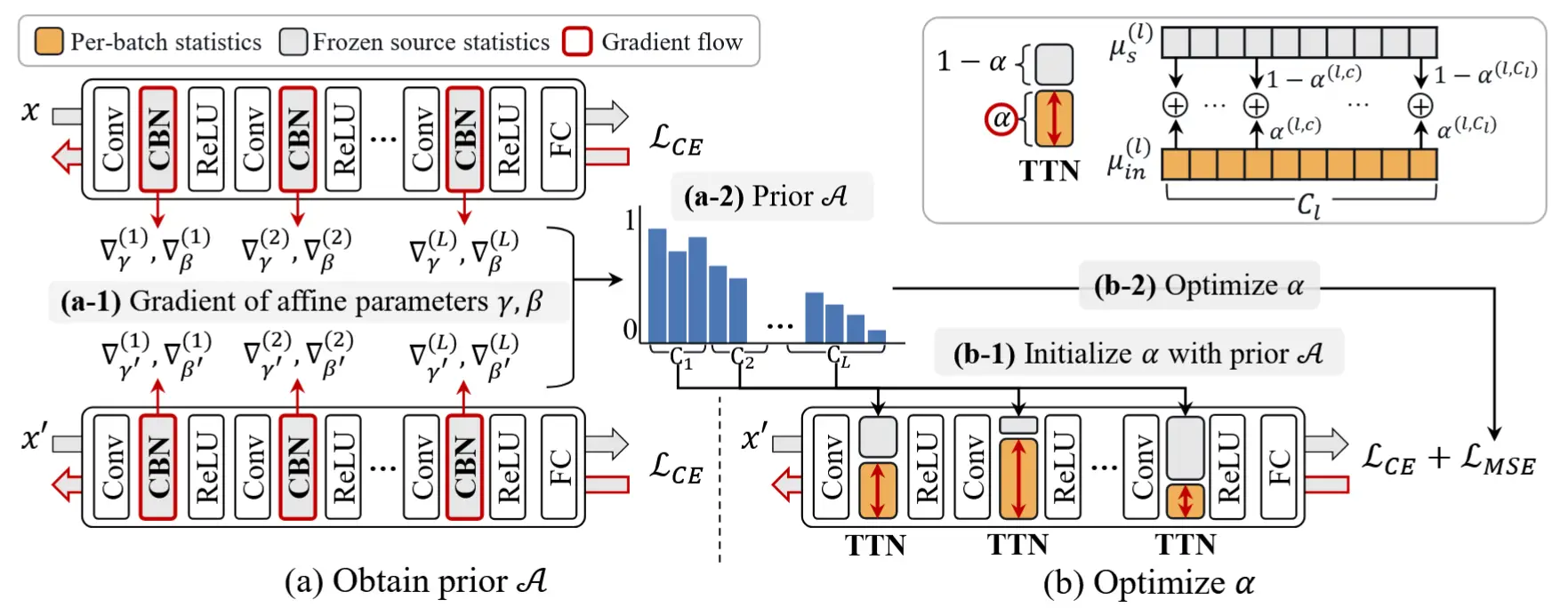
  • 论文 - 《CAFA: Class-Aware Feature Alignment for Test-Time Adaptation》
  • 关键词 - 特征对齐、类别感知、TTA、高斯分布、马氏距离

摘要

  • 研究问题：测试时适应TTA，一种可能的方法是将测试样本的表示空间与源分布对齐（即特征对齐）。然而，在适应过程中无法访问带标签的源数据使得实现具有挑战性。
  • 本文工作
    • 基于上述观察，作者提出了一种简单有效的特征对齐方法 - 类别感知特征对齐（Class-Aware Feature Alignment, CAFA）。
    • 该方法同时实现了以下两点：
      • 1）鼓励模型以类别判别的方式学习目标表示；
      • 2）有效缓解测试时的分布偏移。

1 引言

  • 源与目标分布对齐
    • 现有研究
      • DANN 直接减少了源分布和目标分布之间的 H-散度。
      • CORAL 则最小化了源数据和目标数据之间二阶统计量的差异。
    • 这些方法在无监督域适应（UDA）任务中有效，但是在TTA中存在局限性：这些对齐方法通常依赖于源数据上的监督损失，从而鼓励模型以类别判别的方式学习目标分布。然而TTA中无法访问源数据。
  • 分析
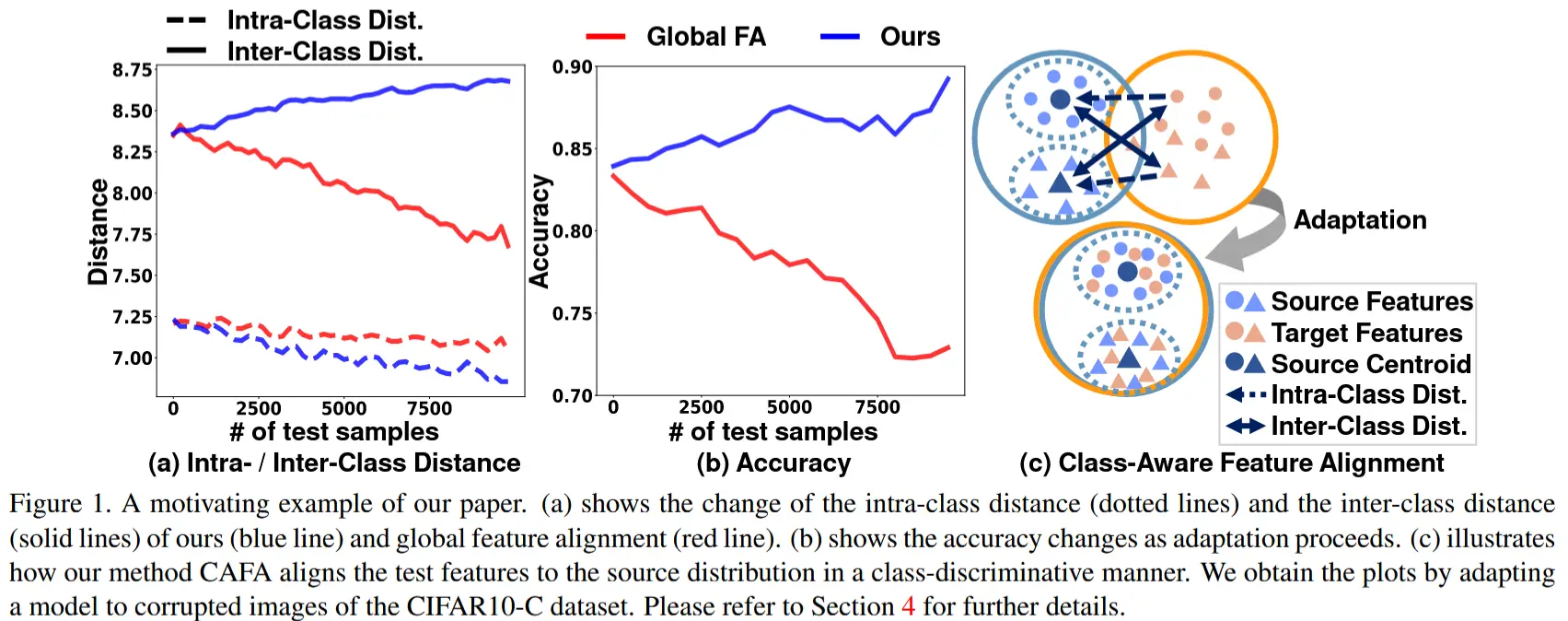
    • 基于这一问题，作者通过表示空间中的两种距离（类内距离和类间距离）分析了特征对齐在 TTA 中的效果。
      • 如图 1 (c) 所示，类内距离（虚线箭头）定义为样本与其真实源类别分布之间的距离，而类间距离（实线箭头）表示样本与其他源类别分布之间的平均距离。
    • 为此，作者首先通过对齐源分布和目标分布的均值和协方差（即全局特征对齐）减少源域和目标域之间领域级差异，结果如图 1 (a) 中的红线所示。类内距离得以减少，这符合期望，但同时也伴随着类间距离的下降。这种效应可能会降低图像分类的准确性（如图 1 (b) 中的红线所示）。

  • 本文方法 - CAFA
    • 同时考虑类内距离和类间距离，将目标特征与预先计算的源特征分布对齐。
    • 首先，预先计算源分布的统计量（即均值和协方差），从预训练网络中估计类别条件高斯分布。
    • 在测试时，我们使用马氏距离（Mahalanobis distance）来：
      • 1）将每个样本与其预测的类别条件高斯分布对齐（即减少类内距离）；
      • 2）强制样本与其他类别条件高斯分布保持区分（即增加类间距离）。
    • 如图1(a)和(b)蓝线所示，应用 CAFA 成功增强了类别判别能力，并且随着适应过程的进行，显著提高了分类精度。
paper41-1.webp

2 方法

2.1 预备知识

TTA相关符号定义跳过。

马氏距离（Mahalanobis Distance）

在这项工作中，我们采用马氏距离来对齐源分布和目标分布。马氏距离衡量的是一个分布与一个样本之间的距离。对于输入图像 ​ x 、特征提取器 ​ g(\cdot) 和高斯分布 ​ \mathcal{N}(\boldsymbol{\mu}, \boldsymbol{\Sigma}) ，马氏距离定义为：

D(x; \boldsymbol{\mu}, \boldsymbol{\Sigma}) = (g(x) - \boldsymbol{\mu})^\top \boldsymbol{\Sigma}^{-1} (g(x) - \boldsymbol{\mu}), \tag{1}

类内/类间距离（Intra-/Inter-class Distance）
为了分析，我们测量类条件源分布与目标样本之间的类内和类间距离。具体而言，我们将类条件高斯分布定义为 ​ P(g_s(x) | y = c) = \mathcal{N}(g_s(x) | \boldsymbol{\mu}_c, \boldsymbol{\Sigma}_c) ，其中 ​ \boldsymbol{\mu}_c, \boldsymbol{\Sigma}_c 是类别 ​ c \in \{1, \dots, C\} 的多元高斯分布的均值和协方差。

对于目标图像 ​ x_t ，类内距离定义为：

D_{\text{intra}}(x_t, y_t) = D(x_t; \boldsymbol{\mu}_{y_t}, \boldsymbol{\Sigma}_{y_t}), \tag{2}

其中 ​ y_t 表示目标图像的真实标签。类似地，类间距离定义为：

D_{\text{inter}}(x_t, y_t) = \frac{1}{C-1} \sum_{c=1}^C \mathbb{1}(y_t \neq c) D(x_t; \boldsymbol{\mu}_c, \boldsymbol{\Sigma}_c), \tag{3}

需要注意的是，实现低类内距离和高类间距离对于提高图像分类准确性非常重要。


2.2 特征对齐中的类别判别性分析

我们比较和分析了三种不同的特征对齐方法，重点关注类内和类间距离。

第一种：全局特征对齐（Global FA）

全局特征对齐在不考虑类别信息的情况下减少源分布和目标分布之间的差异。给定源高斯分布 ​ \mathcal{N}(g_s(x_s) | \boldsymbol{\mu}_s, \boldsymbol{\Sigma}_s) ，全局特征对齐损失 ​ \mathcal{L}_{\text{FA}} 定义为：

\mathcal{L}_{\text{FA}} = \| \boldsymbol{\mu}_s - \hat{\boldsymbol{\mu}}_t \|_2^2 + \| \boldsymbol{\Sigma}_s - \hat{\boldsymbol{\Sigma}}_t \|_F^2, \tag{4}

其中 ​ \boldsymbol{\mu}_s, \boldsymbol{\Sigma}_s 表示不考虑类别信息的源特征均值和协方差，而 ​ \hat{\boldsymbol{\mu}}_t, \hat{\boldsymbol{\Sigma}}_t 表示从一批测试样本中估计出的均值和协方差。​ \| \cdot \|_2 和 ​ \| \cdot \|_F 分别表示欧几里得范数和弗罗贝尼乌斯范数。如图 1 (a)（红色线条）所示，虽然全局特征对齐显著减少了类内距离，但它同时也伴随着类间距离的显著下降，而类间距离需要较高才能实现合理的图像分类准确性。图 1 (b)（红色线条）显示了准确性下降。


第二种：考虑类别信息

为了应对这一问题，我们在对齐特征时考虑类别信息。以类别方式对齐源分布和目标分布是一种直接的方法。然而，在测试时，每个类别在小批量中只有很少的样本可以精确估计测试数据的类条件分布。因此，使用马氏距离将单个测试样本与预测类别的源类条件分布对齐。 需要注意的是，作者将每个样本的预测类别作为其真实标签的代理，因为无法访问真实的标签。具体而言，给定源类条件高斯分布 ​ \mathcal{N}(\boldsymbol{\mu}_c, \boldsymbol{\Sigma}_c) ，最小化类内距离的损失 ​ \mathcal{L}_{\text{intra}} 定义为：

\mathcal{L}_{\text{intra}} = \frac{1}{N} \sum_{n=1}^N D_{\text{intra}}(x_{t,n}, \hat{y}_{t,n}), \tag{5}

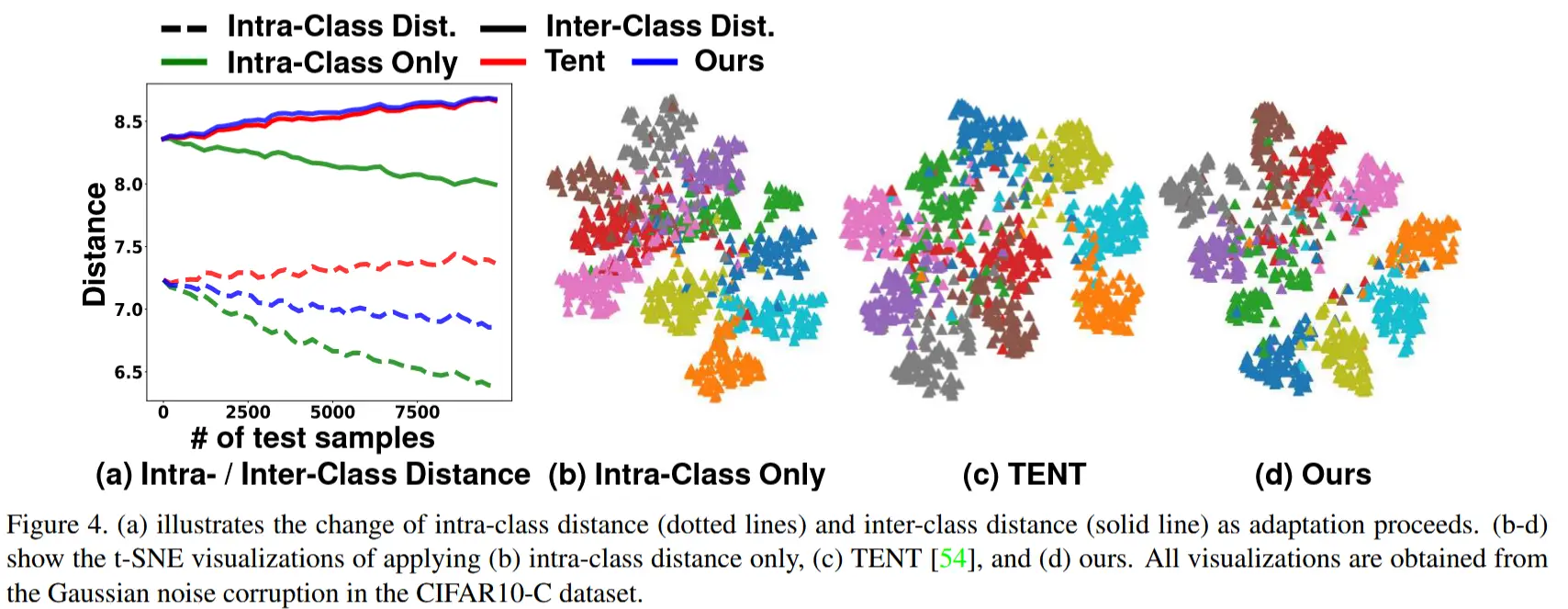
其中 ​ \hat{y}_{t,n} 表示目标样本 ​ x_{t,n} 的预测类别，​ N 表示目标样本的数量。尽管利用 ​ \mathcal{L}_{\text{intra}} 能够有效减少类内距离，但它仍然会降低类间距离，如图 4 (a)（绿色线条）所示。

paper41-2.webp

2.3 CAFA：类别感知特征对齐

第三种：类别感知特征对齐（CAFA）

源统计量的预计算

如图 2 的预处理阶段所示，我们使用预训练的特征提取器 ​ g_s(\cdot) 对源训练样本 ​ (x_s, y_s) 计算 ​ C 个类条件高斯分布 ​ P(g_s(x_s) | y = c) = \mathcal{N}(g_s(x_s) | \boldsymbol{\mu}_c, \boldsymbol{\Sigma}_c) ，公式如下：

\boldsymbol{\mu}_c = \frac{1}{N_c} \sum_{n=1}^{N_c} g_s(x_{s,n_c}), \\ \boldsymbol{\Sigma}_c = \frac{1}{N_c} \sum_{n=1}^{N_c} (g_s(x_{s,n_c}) - \boldsymbol{\mu}_c)(g_s(x_{s,n_c}) - \boldsymbol{\mu}_c)^\top, \tag{6}

其中 ​ N_c 表示类别 ​ c 的训练样本数量，​ x_{s,n_c} 表示类别 ​ c 的训练样本。

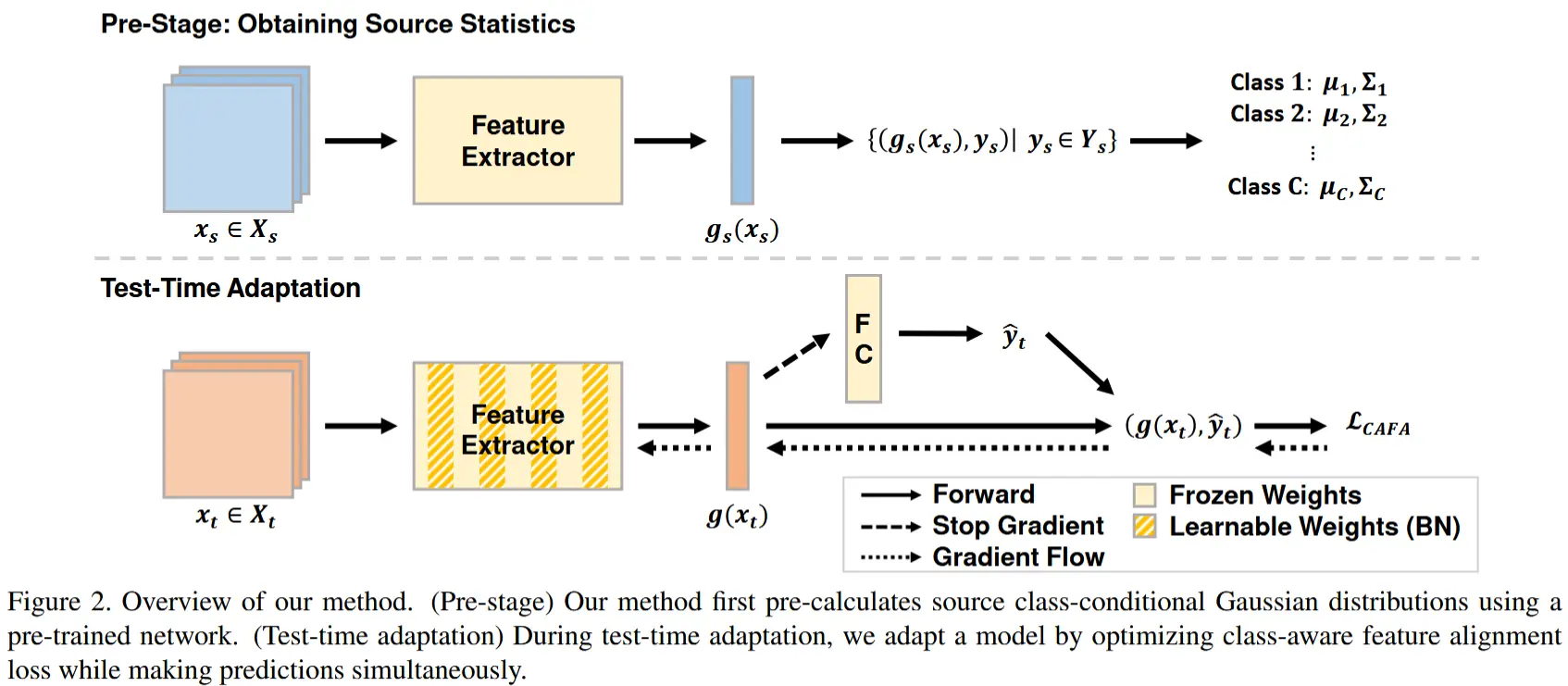
paper41-3.webp

测试时适应

利用源类条件分布 ​ P(g_s(x_s) | y = c) ，我们在测试时执行类别感知特征对齐，如图 2 的测试时适应阶段所示。我们使用预训练网络的权重初始化模型，并在考虑类内和类间距离的情况下对目标数据进行适配。我们的最终损失 ​ \mathcal{L}_{\text{CAFA}} 定义为：

\mathcal{L}_{\text{CAFA}} = \frac{1}{N} \sum_{n=1}^N \log \frac{D_{\text{intra}}(x_{t,n}, \hat{y}_{t,n})}{\sum_{c=1}^C D(x_{t,n}; \boldsymbol{\mu}_c, \boldsymbol{\Sigma}_c)}. \tag{7}

如前面图 4 （a） 所示（蓝线），最终损失通过减小类内距离和扩大类间距离，以理想的方式对齐源和目标分布。


TTA 论文笔记