论文笔记《TTA杂记（二）》

论文笔记《TTA杂记（二）》

Administrator 24 2025-05-06
  • 本文简单记录了最近阅读的经典的TTA方法，细节比较含糊，论文包括：NOTE、TTN、CoTTA

一、NOTE

  • 论文 - 《NOTE: Robust Continual Test-time Adaptation Against Temporal Correlation》

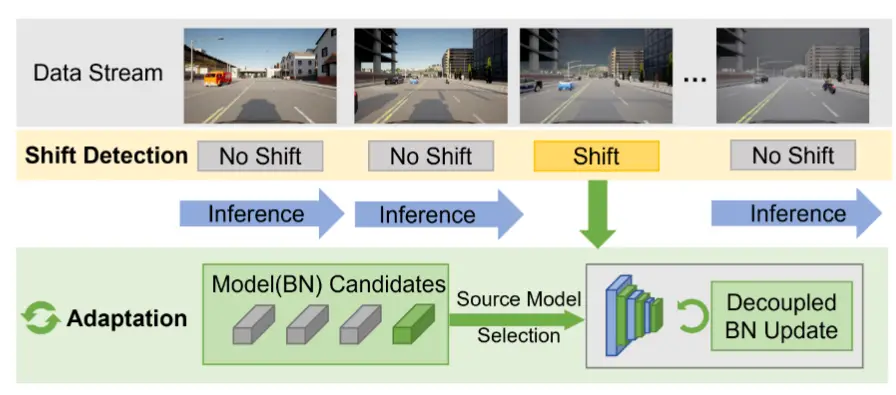
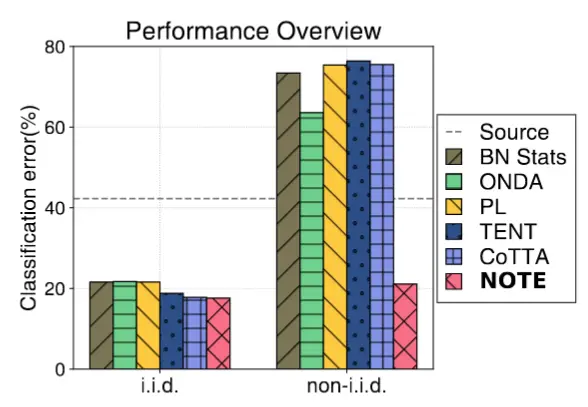
作者的动机非常简单，就是考虑到现实场景中测试数据流往往具有时间相关性，而不是过去工作中假设的独立同分布，如图可以看到对于非独立同分布的场景下，过去的方法性能下降非常明显。

paper42-1.webp

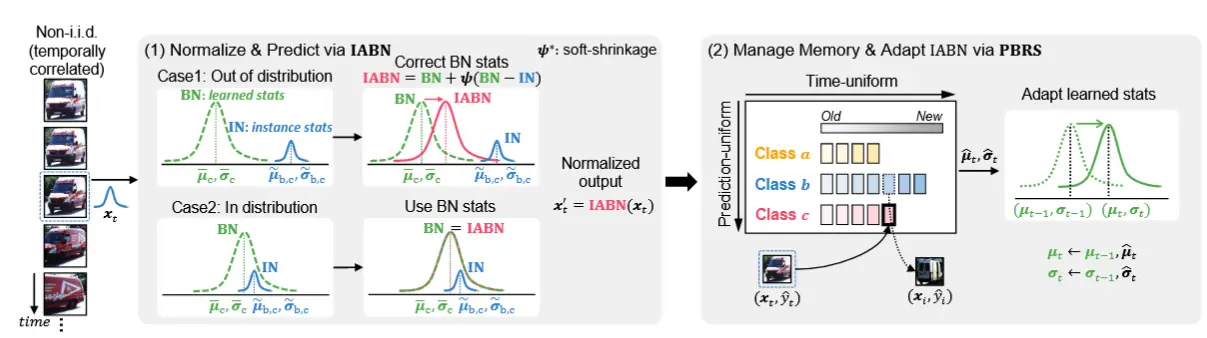
作者提出的NOTE由两个部分组成：Instance-Aware Batch Normalization (IABN) 和 Prediction-Balanced Reservoir Sampling (PBRS)。整体结构如下图所示，最左边是具有时序关联的输入。中间是IABN，通过BN层的均值方差代表源域特征，对每个实例计算统计信息，如果和源域差别不大则不移动；如果和源域差别较大，则通过一个 ​\psi 来校正统计量。右边是PBRS，设置一个缓冲区来存储遇到的测试样本，同时考虑预测类别和时间采样的均匀性，消除时许相关的影响，同时使用指数移动平均来更新均值方差。

paper42-2.webp

1.1 IABN

IABN 的核心思想是基于 实例级统计量（instance-wise statistics）来进行归一化，而不是像传统 BN 那样依赖于批次级统计量。具体来说：

  1. 实例级统计量：对于每个样本 ​b ，计算其特征图 ​\mathbf{f}_{b, c, l} 的实例级均值 ​ \tilde{\mu}_{b, c} 和方差 ​ \tilde{\sigma}^2_{b, c} 。
  2. 统计量校正：为了确保实例级统计量能够反映全局分布，同时避免过度白化，IABN 提出了一种校正机制，将实例级统计量与全局统计量结合使用。

1.1.1 实例级统计量

对于特征图 ​\mathbf{f} \in \mathbb{R}^{B \times C \times L} ，（BCL分别是批次大小、通道数、特征维度）

对于每个样本 ​ b 和每个通道 ​c ，计算实例级均值和方差：

\tilde{\mu}_{b, c} := \frac{1}{L} \sum_l \mathbf{f}_{b, c, l}, \quad \tilde{\sigma}^2_{b, c} := \frac{1}{L} \sum_l (\mathbf{f}_{b, c, l} - \tilde{\mu}_{b, c})^2. \tag{3}

1.1.2 样本均值和方差的方差

假设实例级均值 ​\tilde{\mu}_{b, c} 和方差 ​\tilde{\sigma}^2_{b, c} 来自总体分布 ​\mathcal{N}(\bar{\mu}_c, \bar{\sigma}^2_c) ，则可以计算样本均值和样本方差的方差：

s^2_{\tilde{\mu}_{b, c}} := \frac{\bar{\sigma}^2_c}{L}, \quad s^2_{\tilde{\sigma}^2_{b, c}} := \frac{2 \bar{\sigma}^4_c}{L - 1}. \tag{4}

这些公式反映了实例级统计量的不确定性，尤其是在小批量或时间相关性较强的情况下。

1.1.3 统计量校正

IABN 提出了一种校正机制，仅在实例级统计量与全局统计量显著不同时才进行调整。具体公式如下：

\mu^{\text{IABN}}_{b, c} := \bar{\mu}_c + \psi(\tilde{\mu}_{b, c} - \bar{\mu}_c; \alpha s_{\tilde{\mu}_{b, c}}), \quad and \quad (\sigma^{\text{IABN}}_{b, c})^2 := \bar{\sigma}^2_c + \psi(\tilde{\sigma}^2_{b, c} - \bar{\sigma}^2_c; \alpha s_{\tilde{\sigma}^2_{b, c}}),

  • ​\bar{\mu}_c 和 ​\bar{\sigma}^2_c 是训练数据的统计量。

  • ​\psi(x; \lambda) 是软收缩函数（soft-shrinkage function），定义为：

    \psi(x; \lambda) = \begin{cases} x - \lambda, & \text{if } x > \lambda \\ x + \lambda, & \text{if } x < -\lambda \\ 0, & \text{otherwise} \end{cases}

  • ​ \alpha 是一个超参数，用于控制校正的强度。

软收缩函数的作用是：

  1. 当实例级统计量与全局统计量差异较大时（即 ​|x| > \lambda），对其进行调整，使其更接近全局统计量。
  2. 当差异较小时（即 ​ |x| \leq \lambda ），保持实例级统计量不变，以保留其局部特性。

最后，IABN 的输出可以描述为：

\text{IABN}(\mathbf{f}_{b,c,:,:}; \bar{\mu}_c, \bar{\sigma}_c^2; \tilde{\mu}_{b,c}, \tilde{\sigma}_{b,c}^2) := \gamma \cdot \frac{\mathbf{f}_{b,c,:,:} - \mu_{b,c}^\text{IABN}}{\sqrt{(\sigma_{b,c}^\text{IABN})^2 + \epsilon}} + \beta.

观察到当 ​\alpha = 0 和 ​\alpha = \infty 时，IABN 分别退化为 Instance Normalization和 Batch Normalization。（作者取值为4）


1.2 PBRS

PBRS的核心思想：借助一个小内存（例如，一个 mini-batch 大小的内存）来模拟从时间相关流中抽取的独立同分布（i.i.d.）样本。

1.2.1 选择存储样本

主要由以下两个部分组成：

  1. 时间均匀采样：采用了水库采样（Reservoir Sampling, RS），这是一种经过验证的随机采样算法，可以在单次遍历数据流时收集时间均匀的数据，而无需提前知道数据的总长度。
  2. 预测均匀采样：首先使用预测标签计算内存中的多数类。然后，用一个新的样本替换多数类中的一个随机实例。

从下面的算法理解会更加直观：

paper42-3.webp

1.2.2 利用存储样本

利用内存中存储的样本，更新 IABN 层中的归一化统计量和仿射参数。虽然 IABN 在一定程度上对分布偏移具有鲁棒性，但在严重分布偏移的情况下，这一假设可能不再成立。因此，作者希望通过 PBRS 在分布偏移的情况下找到更好的 ​\mu, \sigma^2 估计值。因此通过指数移动平均更新归一化统计量，即均值 ​\mu_t 和方差 ​\sigma_t^2：
(a) ​\mu_t = (1 - m)\mu_{t-1} + m\frac{N}{N-1}\hat{\mu}_t
(b) ​\sigma_t^2 = (1 - m)\sigma_{t-1}^2 + m\frac{N}{N-1}\hat{\sigma}_t^2
其中 ​m 是动量项，​N 是内存的大小。

进一步地，通过单次反向传播并结合熵最小化来优化仿射参数（缩放因子 ​\gamma 和偏置项 ​\beta ）。注意，IABN 层每收到 ​N 个测试样本时会使用内存中的 ​N 个样本进行适应（​N =64）。


二、TTN

  • 论文 - 《TTN: A DOMAIN-SHIFT AWARE BATCH NORMALIZATION IN TEST-TIME ADAPTATION》

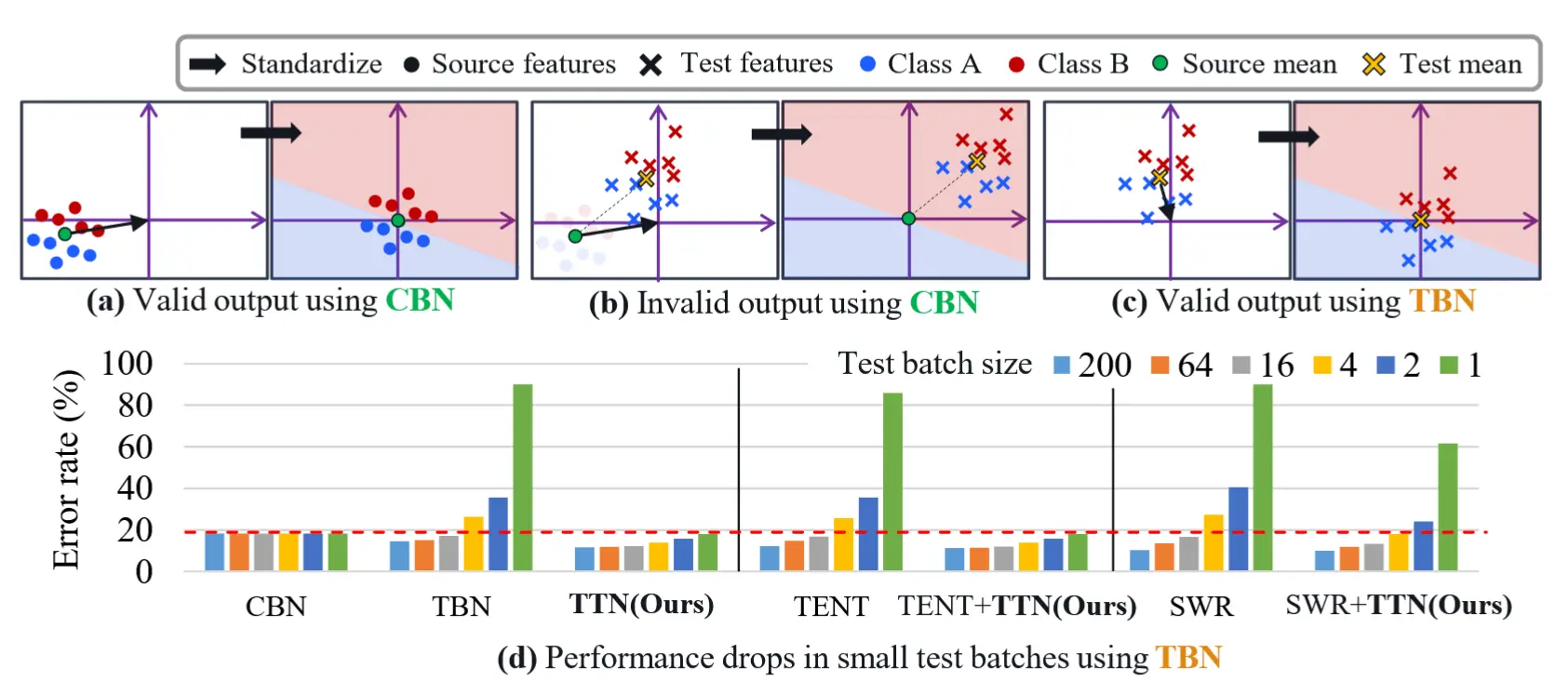
本文的动机就是作者认为CBN和TBN是一个权衡的关系，没有真正利用BN优化性能，如图1所示，具体来说：

  1. Conventional BatchNorm 在训练时使用源域数据的统计量（均值、方差），在测试时也固定这些统计量。当测试数据分布与源域不一致时，特征被错误地标准化到“非预期”的空间。
  2. Transductive BatchNorm 在测试时直接使用当前 batch 的统计量来标准化特征，动态调整 BN 层中的 running mean/var。但是对小批量非常敏感，在连续变化的数据流中表现不佳。
paper42-4.webp

2.1 TTN 整体架构

如图2所示，TTN在预训练和测试时中间引入了一个Post-train阶段，这个阶段作者首先将模型CBN替换成TTN，TTN可以看作是一个CBN和TBN的线性插值，通过参数 ​\alpha 来控制源统计信息和目标统计信息在BN中的权重。在Post-train阶段利用部分训练数据来确定最优的参数 ​\alpha，在测试阶段冻结该参数。

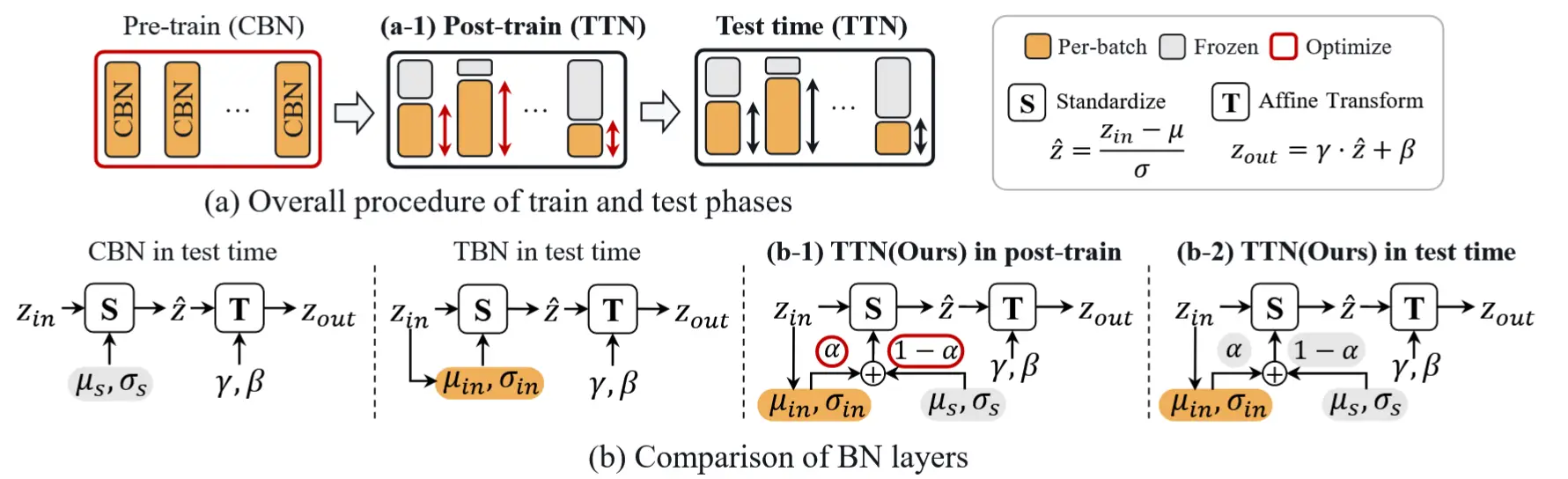
paper42-5.webp

TTN的归一化计算特征公式如下：

\tilde{\mu} = \alpha \mu + (1 - \alpha) \mu_s, \quad \tilde{\sigma}^2 = \alpha \sigma^2 + (1 - \alpha) \sigma_s^2 + \alpha (1 - \alpha) (\mu - \mu_s)^2,

2.2 Post-train

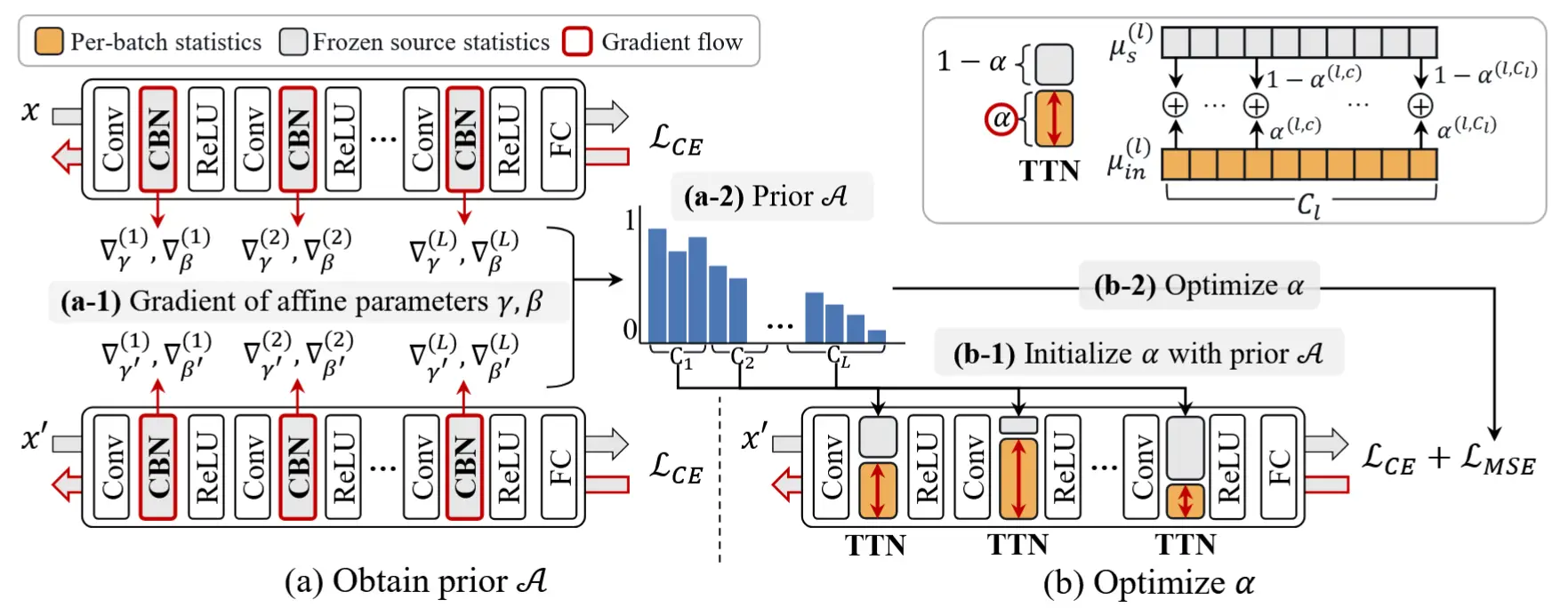
整个Post-train分成两个阶段，如下图所示，stage-1利用增强和原始源数据计算BN层仿射参数梯度的差异（通过梯度距离函数衡量），较大差异的BN层认为对域偏移敏感，得到先验A；stage-2将BN换成TTN，利用交叉熵和均方差损失开始优化 ​\alpha。

paper42-6.webp

三、CoTTA

  • 论文 - 《Continual Test-Time Domain Adaptation》

动机：现有TTA方法主要是利用伪标签更新模型和利用熵正则化提升预测置信度，它们假设测试数据来自静态目标域，然而在持续变化的环境中可能表现不稳定，原因如下：

  1. 伪标签不可靠：生成的伪标签更容易受到噪声干扰，早期的预测错误容易传播，进而导致误差累积。
  2. 灾难性遗忘 ：当模型长时间适应新的数据分布时，原本从源域学到的知识可能被覆盖，从而导致灾难性遗忘

3.1 CoTTA概述

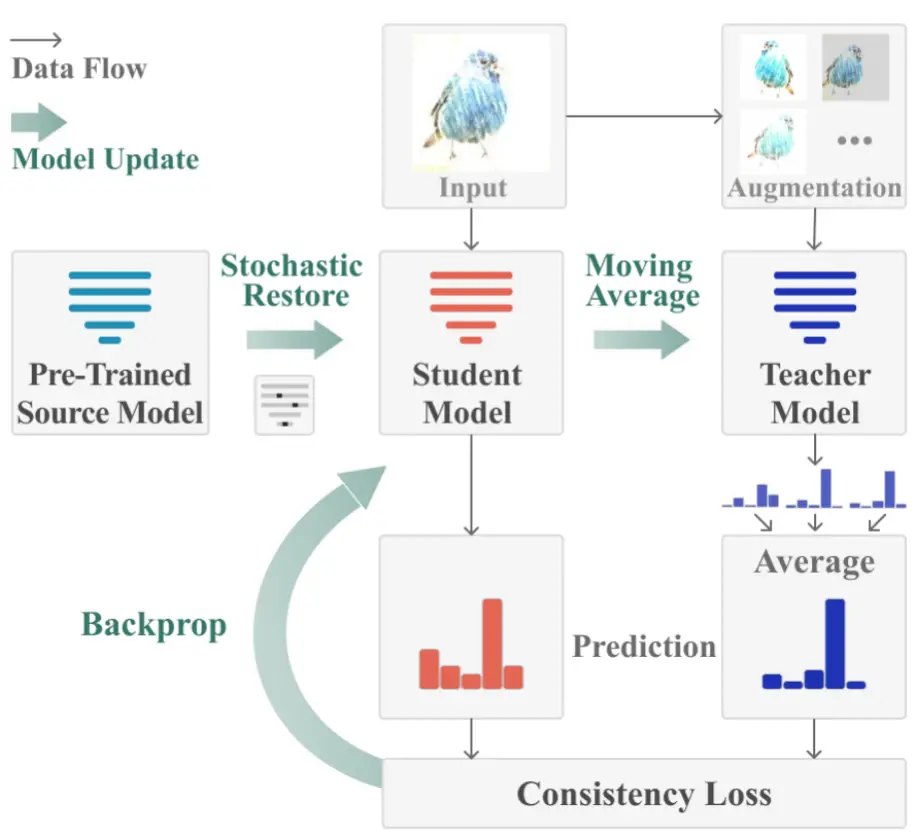
如图2为方法的整体流程图，主要有两个目的：缓解误差累积和避免灾难性遗忘。包含以下步骤：

  1. Weight-Averaged Teacher Model，用于提升伪标签质量，使用一个基于移动平均的教师模型来生成更准确的伪标签。
  2. Augmentation-Averaged Predictions，对于与源域差异较大的测试数据，进一步采用多视角数据增强，并对增强后的预测结果进行平均，从而进一步提升伪标签的准确性。
  3. Stochastic Restore，在每次迭代中随机恢复网络中一小部分神经元的权重 到源域预训练状态。有助于在长期适应过程中保留源域知识，避免灾难性遗忘。
paper42-7.webp

3.2 权重平均伪标签

受权重平均模型通常比最终模型更准确这一观察的启发，作者使用一个权重平均教师模型 ​f_{\theta'} 来生成伪标签。

教师网络被初始化为与源域预训练网络相同。在时间步 ​t，首先由教师模型生成伪标签 ​\hat{y}_t'^T = f_{\theta'}(x_t^T)。然后，学生模型 ​f_{\theta_t} 通过学生和教师预测之间的交叉熵损失进行更新：

\mathcal{L}_{\theta_t}(x_t^T) = -\sum_c \hat{y}_{tc}'^T \log \hat{y}_{tc}^T, \tag{1}

其中，​\hat{y}_{tc}'^T 是教师模型软伪标签预测中类别 ​c 的概率，而 ​\hat{y}_{tc}^T 是学生的预测。该损失强制教师和学生预测之间的一致性。

在使用公式 (1) 更新学生模型 ​\theta_t \to \theta_{t+1} 后，使用指数移动平均法根据学生权重更新教师模型的权重：

\theta_{t+1}' = \alpha \theta_t' + (1-\alpha) \theta_{t+1}, \tag{2}

其中 ​\alpha 是平滑因子。对于输入数据 ​x_t^T，最终预测是 ​\hat{y}_t'^T 中概率最高的类别。

  • 权重平均一致性的优势
    • （1）通过使用通常更准确的权重平均预测作为伪标签目标，受到的误差累积影响较小。
    • （2）均值教师预测 ​\hat{y}_t'^T 编码了过去迭代中的模型信息，因此在长期持续适应中不太容易发生灾难性遗忘，并能提升对新未知域的泛化能力。

3.3 增强平均伪标签

（难点）不同的增强策略通常是手动设计的或通过搜索确定的，针对不同的数据集进行优化。在持续变化的环境中，测试分布可能会发生显著变化，这可能导致增强策略失效。

在这里，考虑到目标域的变化，并通过预测置信度来近似领域差异。只有当领域差异较大时，才会应用增强操作，以减少误差累积。

\tilde{y}_t'^T = \frac{1}{N} \sum_{i=0}^{N-1} f_{\theta_t'}(\text{aug}_i(x_t^T)), \tag{3}
y_t'^T = \begin{cases} \hat{y}_t'^T, & \text{if } \text{conf}(f_{\theta_0}(x_t^T)) \geq p_{th} \\ \tilde{y}_t'^T, & \text{otherwise}, \end{cases} \tag{4}

其中，​\tilde{y}_t'^T 是教师模型的增强平均预测，​\hat{y}_t'^T 是教师模型的直接预测，​\text{conf}(f_{\theta_0}(x_t^T)) 是源预训练模型对当前输入 ​x_t^T 的预测置信度，而 ​p_{th} 是置信度阈值。

通过使用预训练模型 ​f_{\theta_0} 在公式 (4) 中计算当前输入 ​x_t^T 的预测置信度，我们尝试近似源域和当前域之间的领域差异。

注意，当置信度较高时，使用教师模型的直接预测；当置信度较低时，使用教师模型的增强平均预测。这是因为持续变化的分布可能导致增强策略失效，同时作者观察到在小领域差距的高置信样本上应用随机增强有时会降低模型性能。

总结来说，利用置信度近似领域差异，并决定何时应用增强操作。学生模型通过精炼后的伪标签进行更新：

\mathcal{L}_{\theta_t}(x_t^T) = -\sum_c y_{tc}'^T \log \hat{y}_{tc}^T, \tag{5}

3.4 随机恢复

**（动机）**长时间的自训练持续适应不可避免地会引入错误并导致遗忘，特别是在遇到数据序列中的强分布偏移时，这一问题尤为突出。自训练可能会进一步强化这些错误预测，并且模型可能由于持续适应而无法恢复。

为了进一步解决灾难性遗忘的问题，作者提出了一种显式恢复源域预训练模型知识的随机恢复方法。

考虑学生模型 ​f_\theta 中的一个卷积层，在时间步 ​t 根据公式 (1) 进行梯度更新后的状态：

x_{l+1} = W_{t+1} * x_l, \tag{6}

其中，​* 表示卷积操作，​x_l 和 ​x_{l+1} 分别表示该层的输入和输出，​W_{t+1} 表示可训练的卷积滤波器。我们提出的随机恢复方法通过以下方式额外更新权重 ​W：

M \sim \text{Bernoulli}(p), \tag{7}
W_{t+1} = M \odot W_0 + (1 - M) \odot W_{t+1}, \tag{8}

其中，​\odot 表示逐元素乘法，​p 是一个较小的恢复概率，​M 是与 ​W_{t+1} 形状相同的掩码张量。掩码张量决定了 ​W_{t+1} 中哪些元素需要恢复到初始权重 ​W_0。


如算法 1 所示，结合精炼后的伪标签和随机恢复，形成了 CoTTA 方法。

paper42-8.webp
TTA 论文笔记