一、Introduction to Edge AI

• 边缘设备在我们的日常生活中是无处不在的和功率广泛的应用：智能手机、机器人、车辆、办公设备、无线电收发器、自动售货机及家庭电器等。
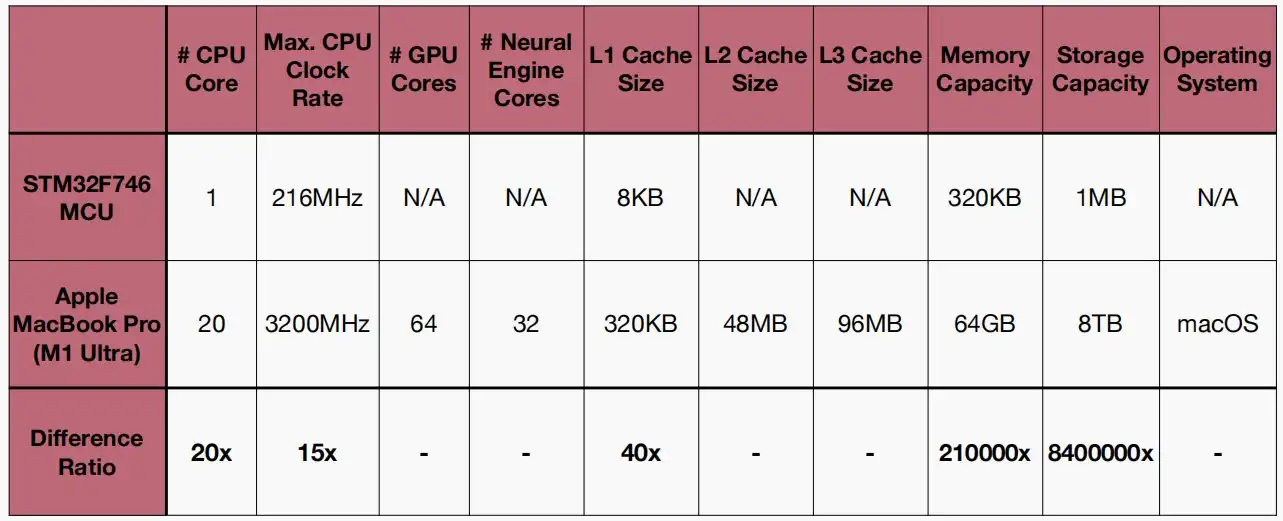
• 从云计算到边缘计算，这一转变凸显了资源有限的挑战。如下图对比了云计算与边缘计算常见设备的资源量。

二、Parallel computing techniques

• 并行计算技术有利于边缘设备利用有限的资源进行机器学习。

  • 并行计算技术不仅有助于小型机器学习，也有助于大型机器学习。对于大型机器学习模型，我们有许多空间在不同维度上并行化计算。
  • 并行计算技术对于推理和训练都很重要。

• 第二章将介绍四种广泛应用于小型和大型机器学习的并行计算技术

  1. Loop optimization循环优化
  2. SIMD(single instruction, multiple data) programming
  3. Multithreading多线程
  4. CUDA programming

Ⅰ、Loop optimization

• Loop optimization主要涵盖以下三个子概念
  • Loop reordering循环重排
  • Loop tiling循环整理
  • Loop unrolling循环展开

Loop reordering循环重排

• 定义：通过重新排序循环的序列来优化局部性。
• 局部性：在操作系统课程中，我们知道系统会将最近访问的块从磁盘装入主存中，以便下一次快速读取，而数组中相邻的数往往存储在同一个块中，一起被装入主存。
• 对于机器学习中，存在大量卷积和矩阵乘法，都涉及到张量的运算。因此考虑循环中的局部性影响，有利于优化运行速度和开销。
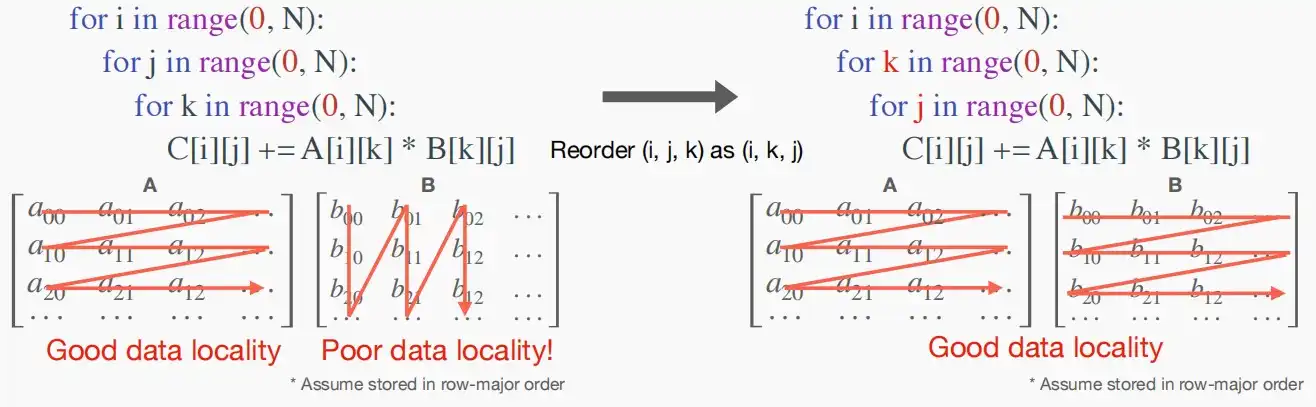
• 如下图中，对于矩阵乘法C = A * B，有两种循环方式(i,j,k)和(i,k,j)，明显后者的局部性更好。
  • 对于(i,j,k)的循环方式，矩阵B局部性较差，每一次访问几乎都会导致缺页中断，降低运行速度。
  • 对于(i,k,j)的循环方式，矩阵A和B的局部性都很好，但是矩阵C的局部性相对较差，但是仍是一行一行访问，权衡之下局部性更好。

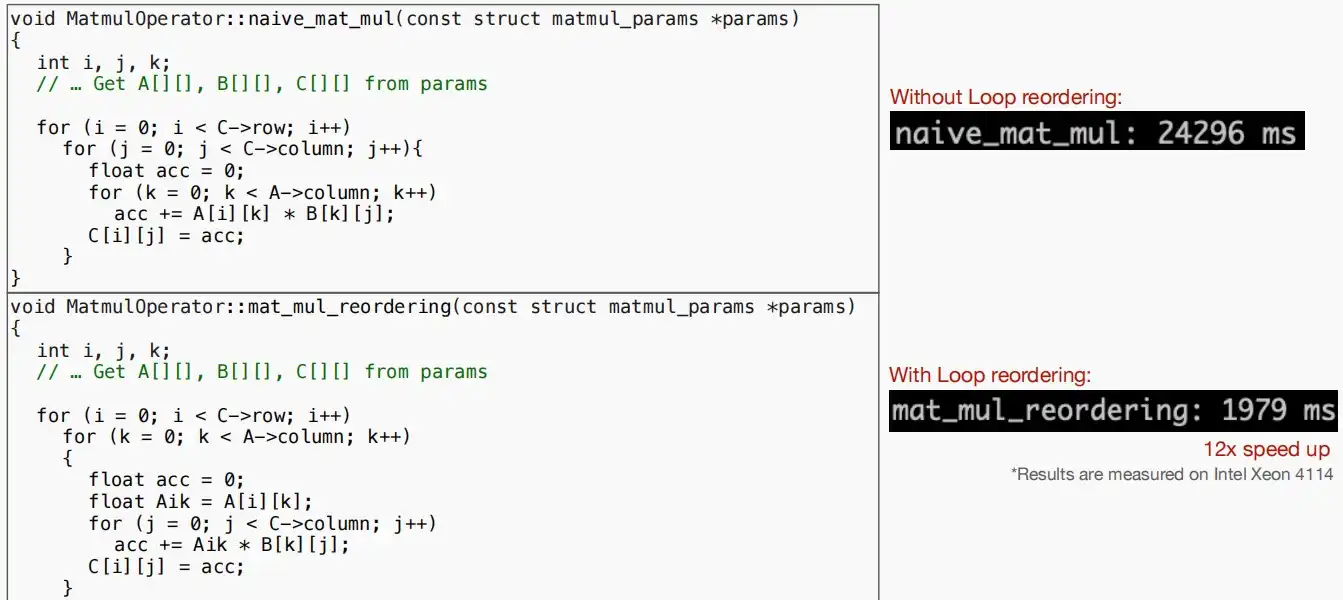
• 从实验数据可以看出，改进后的运行时间从24296ms降低至1979ms。可见Loop reordering对程序局部性的提升效果显著。

Loop tiling循环整理

• 定义：通过划分循环的迭代空间来减少内存访问。
• 如果数据比缓存大小大很多会怎么样？
  • 缓存中的数据被再次使用前被释放，导致缺页中断次数增加。
• Loop tiling循环整理如何减小缺页中断
  • 分区循环迭代空间
  • 使得循环中的访存数据适应缓存大小
  • 确保数据在被再次使用前留在缓存中

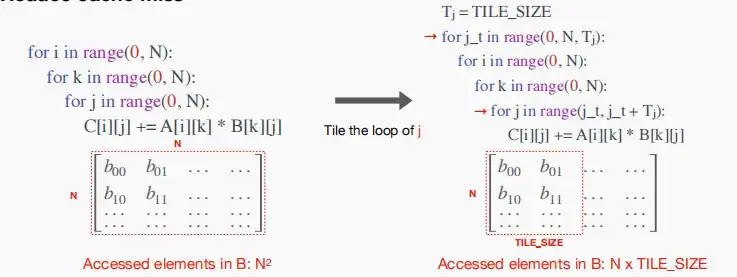
• 如下三张图，对(i,k,j)依次循环进一步优化，依次对(j,k,i)进行分块处理，划分为大小为TILE\_SIZE的块，使得每次访问的大小满足小于缓存大小，减少缺页中断。

  • 对j进行分块处理，划分为每次遍历大小为TILE\_SIZE，则矩阵B每次访问的大小从N^2变为N*TILE\_SIZE。
  • 对k也进行分块处理。则矩阵B每次访问的大小变为TILE\_SIZE^2，矩阵A每次访问的大小变为N*TILE\_SIZE。
  • 对i进行分块处理，则矩阵A每次访问的大小变为TILE\_SIZE^2，且矩阵C每次访问的大小也变为TILE\_SIZE^2。

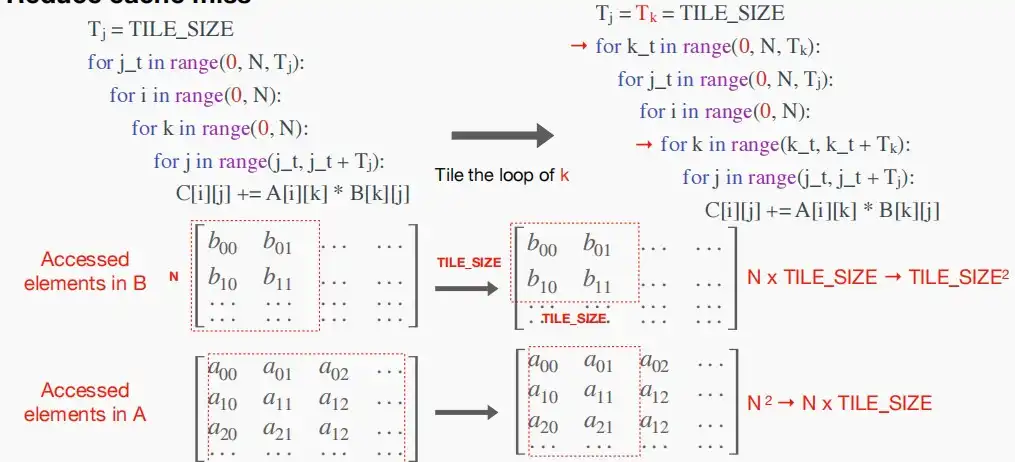
• TILE\_SIZE的大小可以根据高速缓存的大小来确定。
• 每次访问的数据大小适配缓存大小->重用缓存中的数据数增加->缓存缺失数下降。

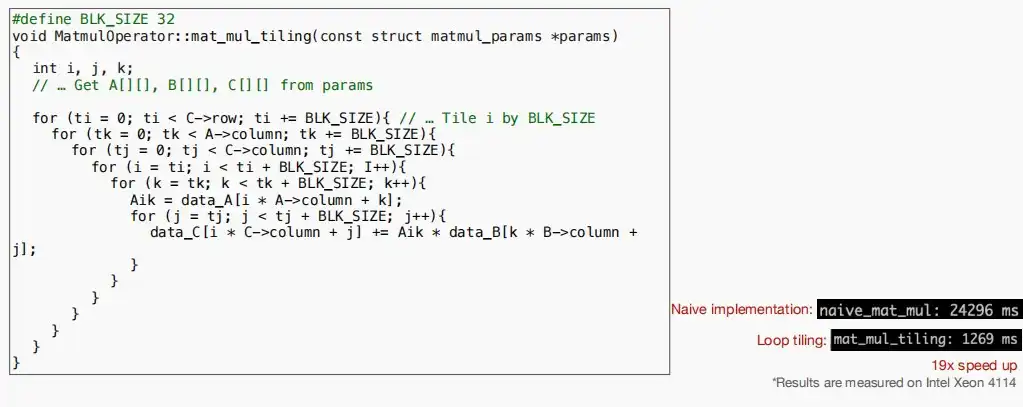
• 多级整理机制：对于存在多级缓存的平台，还可以进一步考虑各级缓存的大小，例如下图中进一步划分j，使得最小的三个循环即每次访问的数据大小等于L1 Cache，最小的四个循环访问数据大小等于L2 Cache。

• 如下图通过六个循环进行循环整理后，运行时间从24296ms降低到1269ms。

Loop unrolling循环展开

• 定义：以牺牲其二进制文件的大小为代价来减少分支开销。
• 循环控制造成的开销
  • 指针的算术操作
  • 循环结束条件测试
  • 分支预测
• 通过循环展开减小的开销
  • 每次重复循环体
  • 权衡二进制大小和减小的开销

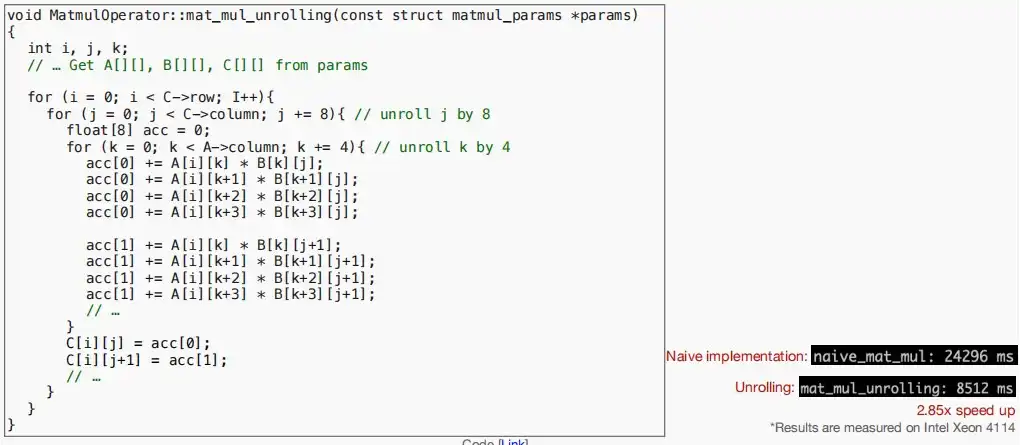
• 如图，对原循环进行改进，每一次循环执行四个步长的k
  • 对指针的算术操作：N^3 -> 1/4N^3
  • 循环结束条件测试：N^3->1/4N^3
  • 最内部循环的代码大小：1->4

• 效果如下

Ⅱ、SIMD programming

• 定义：对多个数据点同时执行相同的操作。通过将同一指令应用于多个数据，使得它们相互同步，避免控制开销和指令开销。
• 关键特点
  • 向量寄存器：可以保存和处理多个数据元素的专用寄存器。
  • 向量操作：用于整个向量的算术和逻辑运算。
• 优点
  • 提高计算吞吐量和速度
  • 提高能效

• 例子：Intel的SSE指令集 & ARM的Neon指令集
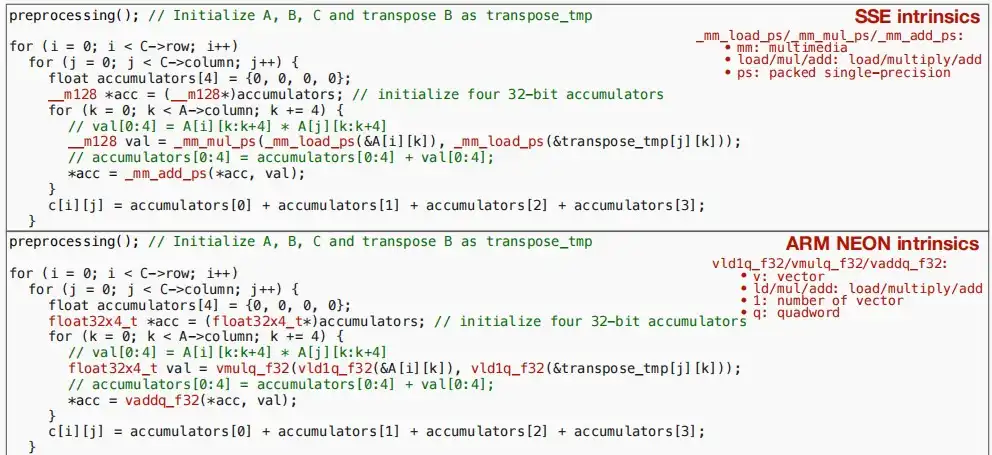
  • SSE和Neon都是SIMD类型的指令集，它们都有类似指令可以一次性处理四个32位操作数的运算。
  • SSE
    • _mm_load_ps、_mm_mul_ps：mm代表多媒体，load代表加载到寄存器，ps代表压缩单精度。
  • Neon
    • vld1q_f32、vmulq_f32：v代表向量、ld表示load，mul表示乘法，1表示向量数，q表示quadword四字。

• 下图是使用SSE和Neon指令进行矩阵乘法的示例代码，需要注意的是transpose_tmp是矩阵B的转置，以实现loop reordering的同样效果。

Ⅲ、Multithreading

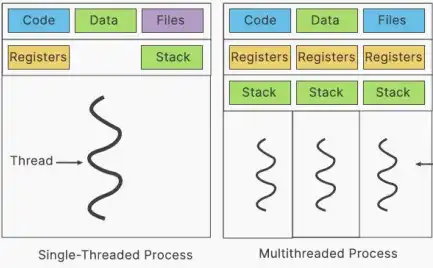
• 定义：多线程是指在单个进程中并发执行多个线程。
• 线程
  • 最小的执行单元是线程，最小的资源分配单元是进程，线程共享进程中的资源。
  • 线程共享相同的内存空间和资源，但它们有自己的堆栈和程序计数器。
  • 不同的线程可以在不同的CPU核心上运行，从而提高性能并允许并行性。

• 多线程的优点
  • 改进的性能：多个线程可以同时执行任务，提高总体程序速度。
  • 响应性：一个程序可以对用户的输入保持响应而不受阻塞。
  • 资源利用率：线程可以共享资源，减少了创建多个进程的开销。
  • 简化的程序结构：多线程可以帮助将复杂的问题分解为更简单、更小的任务。

• 介绍两种实用的用于编写多线程程序的库-Pthreads和OpenMP
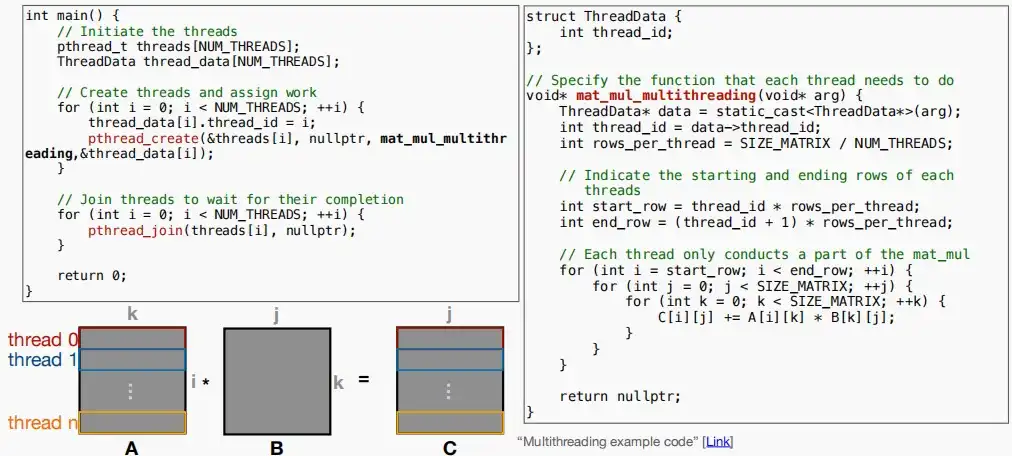
• 使用多线程时加速矩阵乘法，需要将矩阵分割成若干部分，每个线程负责其中一部分。通常按照行分割矩阵A，减少线程间通信，使其工作相互独立。

• 如下图，通过Pthreads库来设计多线程，加速矩阵乘法的代码示例。优化后运行时间从24296ms降低到5864ms。

• OpenMP
  • 特点
    • 一个共享内存的并行编程模型
    • 适用于C,C++,Fortran
    • 可跨不同平台和操作系统
    • 易于与现有代码集成
    • 适用于各种处理器
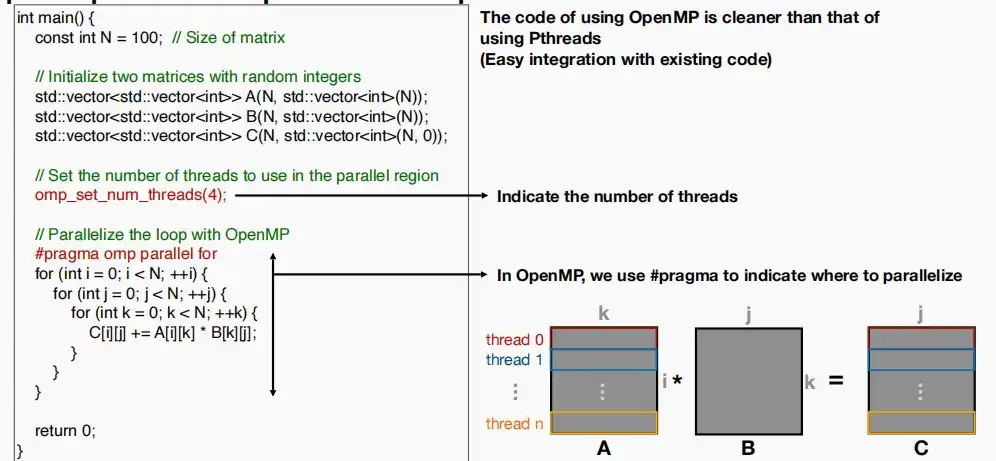
  • 如下图，通过OpenMP库来设计多线程，加速矩阵乘法的代码示例，相比于Pthreads代码更加简洁，仅需两行即可实现并行。

Ⅳ、CUDA programming

• 定义：使用gpu来加速计算。
• 介绍
  • 图形处理单元（GPU）提供了更高的指令吞吐量和内存带宽。
  • CUDA是由英伟达在2006年推出的，作为一个通用的并行计算平台和编程模型，它利用了Nvidia gpu中的并行计算引擎。
  • CUDA类似C语言，用来表示使用计算模式的硬件接口在gpu上运行的程序。
• 如图为CUDA线程的层次结构
  • 绿色的为线程块，大小为2×3；橙色的为其中一个线程块中的线程，大小为3×4。因此总共有72个cuda线程。

• 如下图是CUDA编程示例代码
  • 上方代码为主机代码，在CPU上串行执行。负责为矩阵ABC分配内存，并启动CUDA线程。
  • 下方代码为CUDA内核代码，在GPU上执并行执行。每个线程从其在块中的位置（threadIdx）和其块在网格中的位置（blockIdx）计算其整体网格线程id。

• 先前我们假设矩阵ABC均已分配，现在重新来了解它们的分配方式。
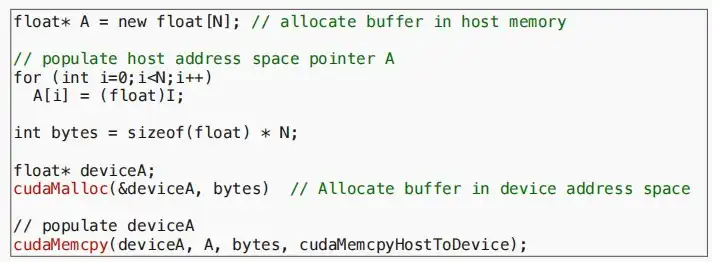
  • CUDA编程中有两个地址，一个是主机地址即CPU内存地址空间，另一个是设备内存地址。数据可以在两个地址空间内移动，但我们希望尽量减少移动。注意，我们无法从主机CPU代码段访问GPU内存。
  • 下图代码中
    • “A[i] = (float)I;”是填充主机地址空间指针A。
    • “cudaMalloc(&deviceA, bytes);”是在设备GPU地址空间中分配缓冲区。
    • “cudaMemcpy(deviceA, A, bytes, cudaMemcpyHostToDevice);”是将数据从CPU复制到GPU。

• 对内核可见的三种不同类型的地址空间
  • 私有内存（每个线程）、共享内存（每个块）、全局内存
    • 私有内存访存最快，空间最小；全局内存访存最慢，空间最大。
  • 不同的地址空间->不同的位置->不同的负载/存储开销

• 如下图，使用CUDA算法加速矩阵乘法，原运行时间24296ms，优化后在GPU运行时间258ms，CUDA内核运行时间6.796ms。

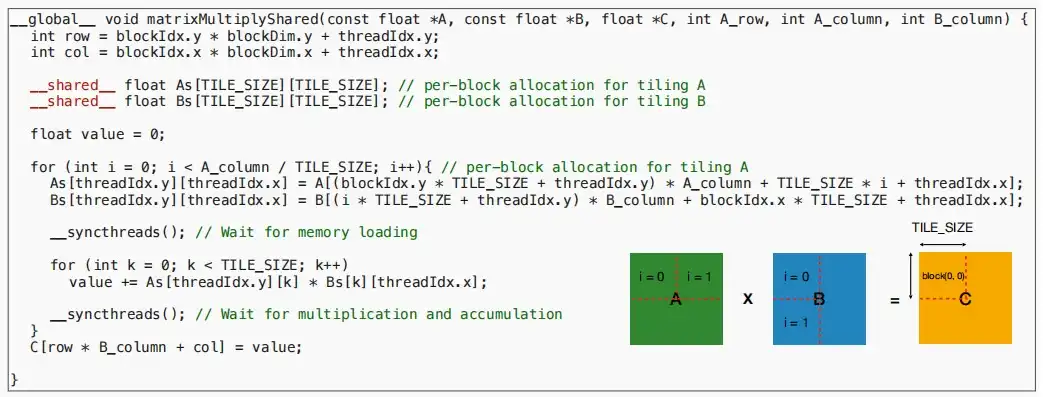
三、Inference optimizations

• 推理优化目的：提高计算速度，减少内存使用
• 本章介绍以下四种技术：
  • Image to Column (Im2col) convolution
  • In-place depth-wise convolution
  • NHWC for point-wise convolution, and NCHW for depth-wise convolution
  • Winograd convolution

Ⅰ、Image to Column (Im2col) convolution

• 定义：重新排列输入数据以直接利用矩阵乘法核。
• Im2col是一种通过广义矩阵乘法（GEMM）实现卷积的技术。

• 下图是原本的卷积操作

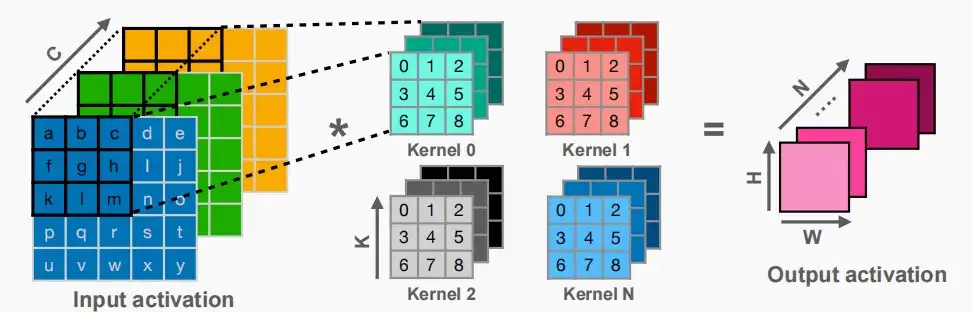
• 利用Im2col技术将输入和内核都变化为矩阵，实际上就是将每次参与运算的两个矩阵展开成一个一维的向量，两个矩阵的乘法变成一维向量的点积，则整个输入和内核的卷积变成两个矩阵的乘法，类似于降维。参考im2col可以更好理解。

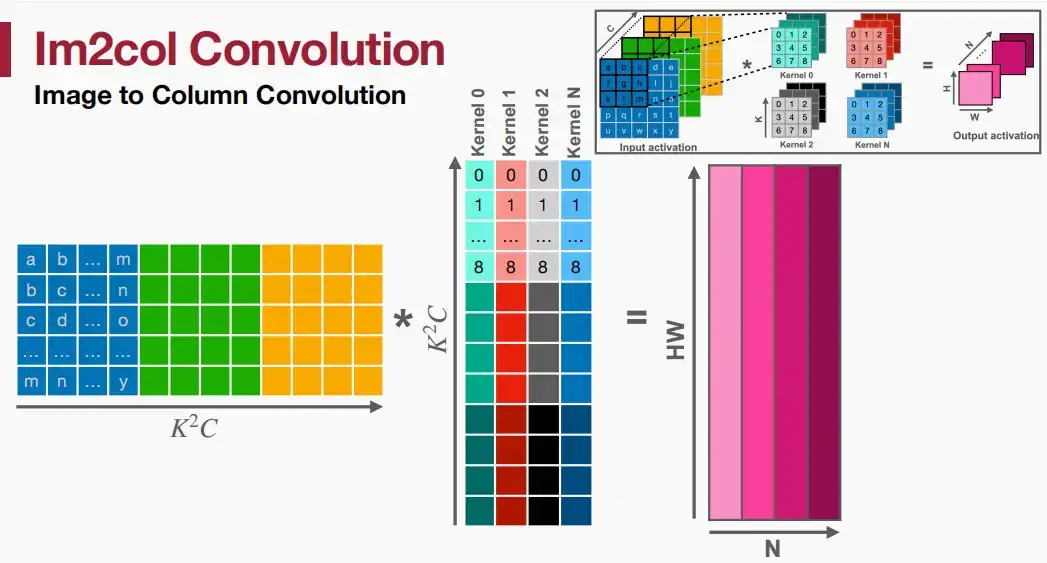
• 优缺点
  • 优：利用经过良好优化的GEMM进行卷积。
  • 缺：增加额外的内存使用（从上图也可以看出，输入激活的大小明显增大，大约2/3的内存重复），隐式GEMM可以解决额外的内存使用问题。

Ⅱ、In-place depth-wise convolution

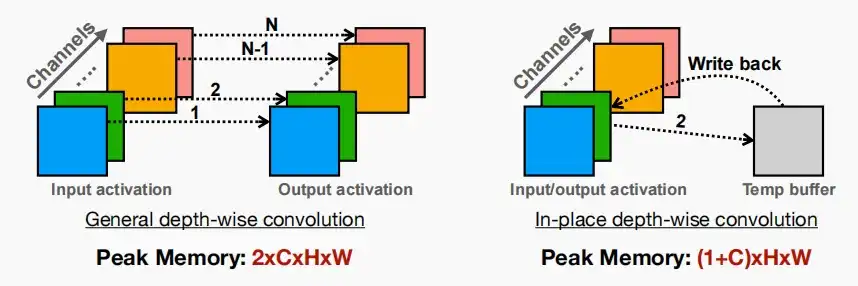
• 定义：重用输入缓冲区写入输出数据，以减少峰值SRAM内存。
• 许多流行的神经网络模型，如MobileNetV2，都具有深度卷积的“反向残差块”，减少了模型大小和FLOPs，但显著增加了峰值内存。
• 为了减少深度卷积的峰值内存，我们使用了带有临时缓冲区的“就位”更新策略。

Ⅲ、How to Choose the Appropriate Data Layout

• 针对不同类型的卷积，利用适当的数据布局。
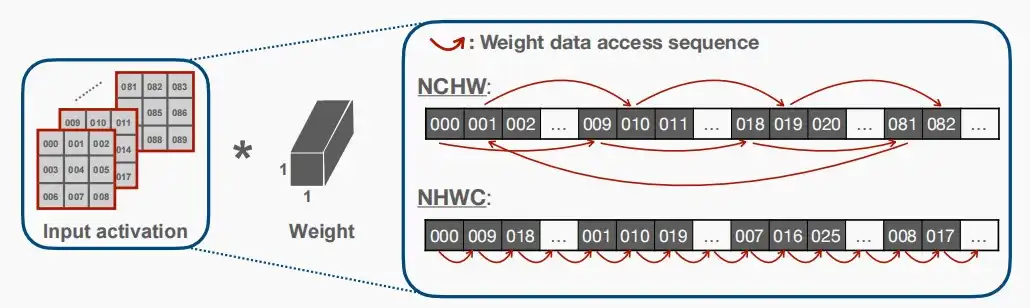
• Use NHWC for Point-wise Convolution
  • 一般来说，由于有更多的顺序访问，NHWC比NCHW在point-wise卷积方面具有更好的局部性。
  • 如下图右框中的权重数据访问顺序，NHWC和NCHW具有不同的存储顺序，对于point-wise卷积显然NHWC连续访问更好。

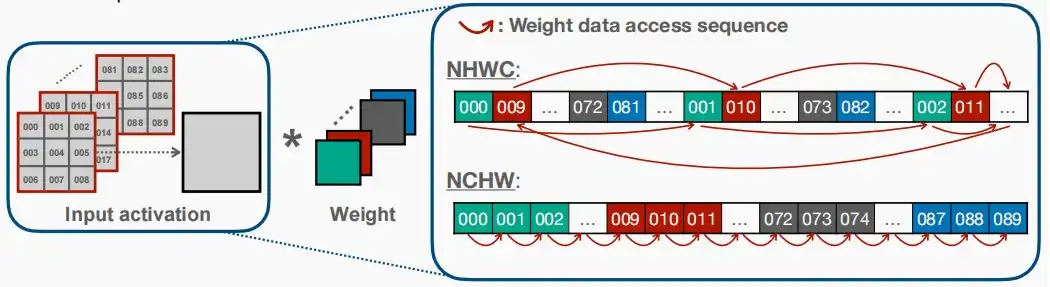
• Use NCHW for Depth-wise Convolution
  • 我们将访问激活，并在NCHW序列中进行深度卷积。
  • 由于有更多的顺序访问，NCHW在深度卷积方面比NHWC具有更好的局部性。

Ⅳ、Winograd convolution

• 减少乘法的次数，以提高卷积的计算速度。
• 具体讲解可以自行搜索Winograd convolution，参考：卷积神经网络中的Winograd快速卷积算法、Fast Algorithms for Convolutional Neural Networks。

---