论文 - 《MOS: MODEL SYNERGY FOR TEST-TIME ADAPTATION ON LIDAR-BASED 3D OBJECT DETECTION》
代码 - Github
关键词 - LiDAR、3D目标检测、TTA、ICLR2025 Oral

摘要

问题背景
- 基于 LiDAR 的 3D 目标检测在实际部署中常因域偏移而导致性能下降。
- 大多数研究集中于跨数据集的偏移，但由传感器差异和天气条件引起的实际损坏问题仍未得到充分探索。
本文方法
- 提出了一种 模型协同（Model Synergy, MOS）策略
  - 该策略 动态选择具有多样化知识的历史检查点，并将它们 组合起来 以最佳适配当前测试批次。
  - 组合由本文提出的 协同权重（Synergy Weights, SW） 指导，SW 对选定检查点进行加权平均，从而减少组合模型中的冗余。
  - SW 通过 评估测试数据上预测边界框的相似性 以及模型库中 检查点对之间特征的独立性 来计算。
  - 为了保持高效且信息丰富的模型库，会 丢弃平均 SW 分数最低的检查点，并用新更新的模型替换它们。
- 考虑了一种更具挑战性的跨损坏场景，即跨数据集偏移与损坏同时发生。
实验
- 我们的方法在三个数据集和八种损坏类型上经过严格测试，相较于现有的测试时适应策略展现了卓越的适应能力，特别是在动态场景和条件下表现出色。值得注意的是，在具有挑战性的跨损坏场景中，我们的方法实现了 67.3% 的性能提升，为适应性提供了一个更全面的基准。

1 引言

cross-curruption 跨损坏
- 过去的工作研究了跨数据集场景（例如从 nuScenes 到 KITTI ）、或者对干净数据集添加扰动（例如从 KITTI 到 KITTI-C ）。
- 然而，在真实场景中，偏移通常并非源自单一因素，这促使我们提出了一种新的混合偏移，称为跨损坏，其中 跨数据集差距和损坏噪声在 3D 场景中共存。
无监督域适应 (UDA) vs. 测试时适应 (TTA)
- UDA 通过 多轮自训练 结合 伪标签技术 对目标数据进行处理，或通过强制源域和目标域数据之间的 特征级对齐 来学习域不变表示。尽管有效，但这些基于 UDA 的方法 需要对预先收集的目标样本 进行离线多轮训练。（耗时、不适用实时数据流场景）
- TTA 主要通过以下两种方式实现：(1) 选择一小部分网络参数进行更新；(2) 使用均值教师模型提供一致的监督信号。
动机：使用均值教师模型的方法平等的对待所有先前检查点
- 2D 目标检测工作：MemCLR (VS 等, 2023) 将 TTA 的思想扩展到基于图像的 2D 目标检测，通过基于 Transformer 的记忆模块提取并优化每个检测目标的感兴趣区域（RoI）特征。
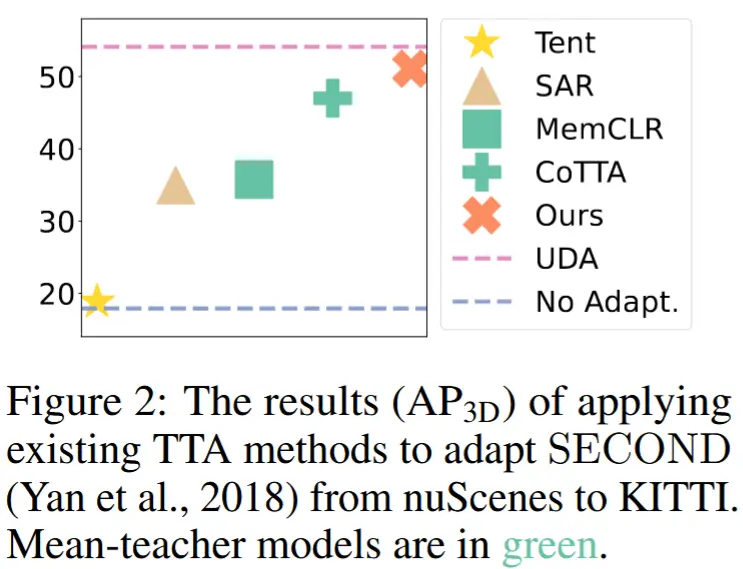
- 针对 3D 检测模型的 TTA 未被探索，因此作者首先调查这些 TTA 技术在 3D 检测任务中的有效性。
  - 如图 2 所示，使用均值教师模型的方法（MemCLR 和 CoTTA）优于其他方法。然而，通过对每个测试样本的移动平均（EMA）平等对待所有先前检查点，教师模型可能无法回顾并利用不同检查点中最重要的知识。
  - 图 3 显示了测试点云 x_{t+1} 和 x_{t+2} 具有非常不同的特征，而教师模型仍然依赖于统一的知识集（即由 EMA 生成的），未能利用针对特定场景定制的先前检查点的相关见解。因此，没有任何教师模型能够完美适配所有目标样本。
- 改进目标：一个最优的“超级”模型应动态组装以适配每个测试批次。

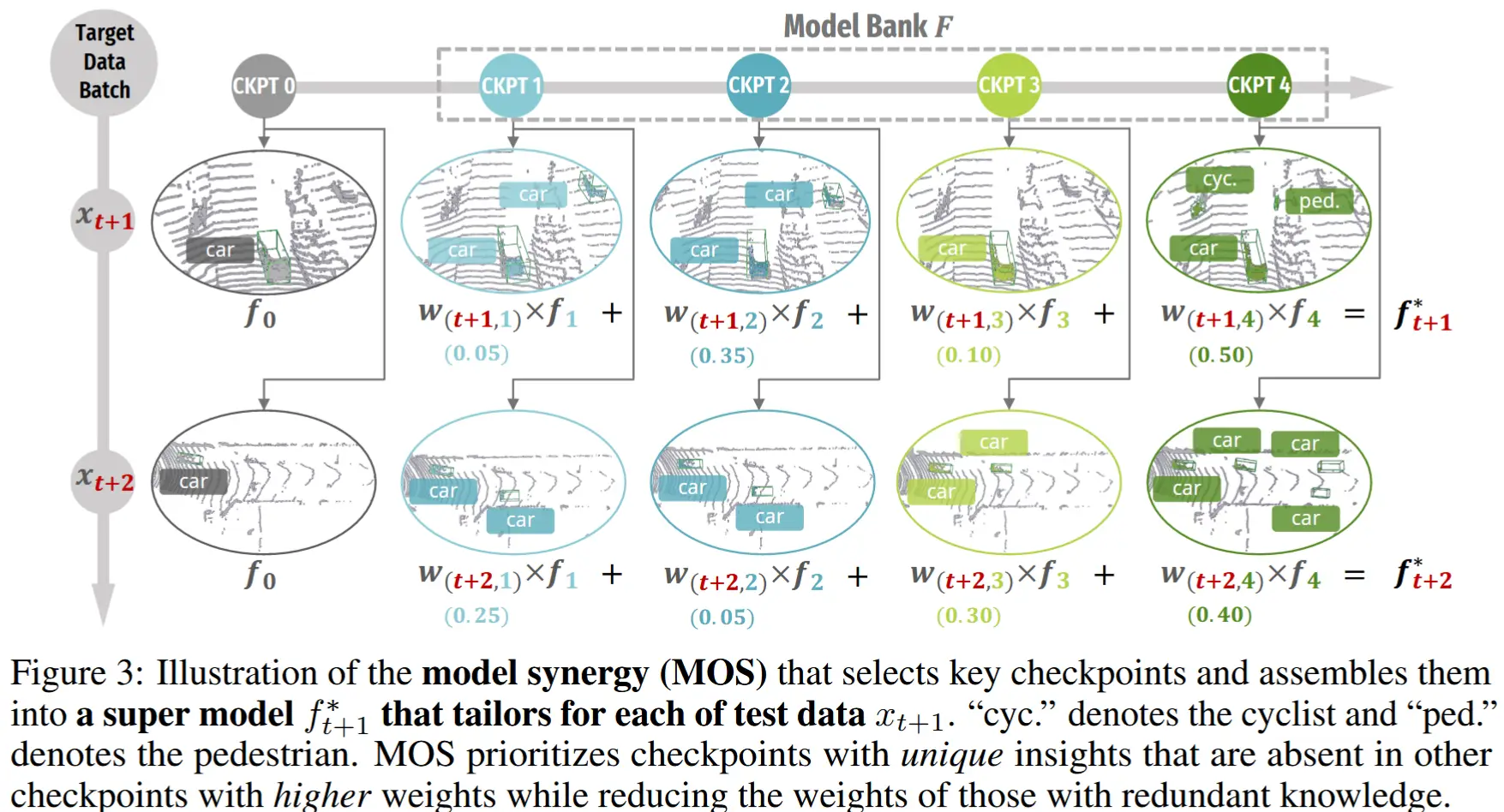
本文方法：模型协同 Model Synergy, MOS
- 基本思想：该策略能够巧妙地选择并组装最适合的先前检查点，形成一个统一的超级模型，利用长期信息来指导当前测试批次数据的监督。
- 如何“选择并组装检查点”？
  - 引入了 协同权重（Synergy Weights, SW） 的概念，通过加权平均先前训练的检查点来促进模型组装。
  - 建立了一个模型协同库（model synergy bank），用于保存 K 个先前适配的检查点。
  - 例如，图 3 中为了组装一个针对 x_{t+1} 的模型，由于冗余的边界框预测，检查点 1 和 3 被分配较低的 SW，而检查点 4 由于有汽车人和行人的概念，被分配较高的 SW。
- 如何“确定最佳的SW”？
  - 将此问题重新表述为求解一个线性方程，目标是创建一个 既多样化又与所有检查点保持相似性 的超级模型，同时 避免对任何特定检查点的偏倚。
  - 这个线性方程的闭式解涉及计算逆 Gram 矩阵，该矩阵量化了检查点对之间的相似性。为此，我们设计了两种针对 3D 检测模型的 相似性函数：
    - (1) 输出级 ，通过匈牙利匹配算法计算 3D 边界框的预测差异；
    - (2) 特征级 ，通过计算拼接特征图的矩阵秩来评估特征独立性。
  - 通过对每个新的测试批次计算这些相似性，我们确定了构建超级模型所需的 SW。随后，这个超级模型生成伪标签，用于在当前时间戳对模型进行单次迭代训练。
- 如何“缓解检查点保存的内存成本”？
  - 引入了一种动态模型更新策略，在添加新检查点的同时移除最不重要的检查点。
  - 实验结果表明，MOS 仅在模型库中保留 3 个检查点的情况下，优于组装最新的 20 个检查点，并且内存消耗减少了 85%。

2 提出方法

2.1 整体框架

（问题定义）

3D 目标检测的测试时适应（TTA-3OD）：当在源数据集上预训练的 3D 检测模型被部署时，由于实际条件的变化，测试点云 (x_t\}_{t=1}^T 可能会发生偏移或损坏，其中 x_t 表示测试数据流中的第 t 个测试点云。TTA-3OD 的最终目标是在推理过程中，通过单次传递将 3D 检测模型适应到一系列目标场景。

（MOS核心思想）

针对每个测试批次 x_t，识别出具有独特知识的最适合的历史模型，并将它们组装成一个超级模型 f_t^*，以促进测试时的模型适应。为此，我们建立了一个大小为 K 的模型库 F = \{f_1, \dots, f_K\}，用于保存和协同之前训练的模型。

（整体框架）

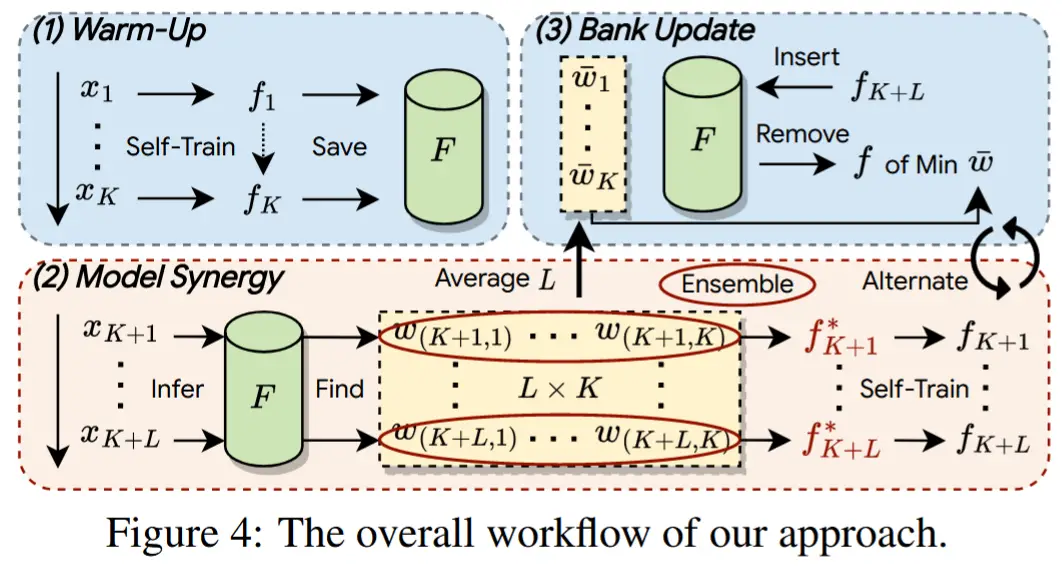
MOS 方法总体工作流程分为三个阶段，如图 4 所示。

阶段 1 ：预热 Warm-up
- 最初，当模型库 \mathbf{F} 尚未填充时，我们通过伪标签自训练的方式使用前 K 个到达的目标批次来训练模型。我们在每个时间戳保存模型为一个检查点，\{f_1, \cdots, f_K\}，并将它们存入 \mathbf{F}，直到其容量达到 K。
阶段 2 ：模型协同 Model Synergy
- 一旦 \mathbf{F} 被填满，对于后续的每个测试批次 x_t，\mathbf{F} 中的检查点被组装成一个超级模型 f_t^* 以生成伪标签 \hat{\mathbf{B}}^t 用于监督。例如，如图 4 的阶段 2 所示，在推断 x_{K+1} 时，我们通过 \mathbf{F} 组装超级模型为 f_{K+1}^* = w_{(K+1,1)}f_1 + \cdots + w_{(K+1,K)}f_K。然后，伪标签 \hat{\mathbf{B}}^{K+1}由 f_{K+1}^* 生成，用于对当前模型 f_{K+1} 进行单次迭代训练。当测试了 L 个批次后，我们更新模型库。
阶段 3 ：模型库更新
- 为了保持模型库 \mathbf{F} 的紧凑性，同时确保每个模型持有独特的知识，我们动态更新 \mathbf{F} 以固定其大小为 K。每测试 L 个批次，我们就用新训练的 f_t 替换 \mathbf{F} 中冗余知识最多的检查点。阶段 2 和阶段 3 交替进行，直至所有目标样本 \{x_t\}_{t=1}^T 均被测试完毕。

2.2 模型协同

阶段 1 比较简单直观，没有详细介绍。

2.2.1 最优协同权重的超级模型组装

对于每个批次 x_t，我们假设存在最优的协同权重 \mathbf{w} \in \mathbb{R}^K，用于线性组装模型库 \mathbf{F} 中的历史检查点为一个超级模型 f_t^*，如下所示：

\mathbf{F} \mathbf{w} = f_t^*. \tag{1}

为了简化表示，我们使用相同的符号 f_t 表示模型参数。最优的协同权重 \mathbf{w} 可以通过 求解以下线性方程 得出：

\mathbf{w} = (\mathbf{F}^T \mathbf{F})^{-1} \mathbf{F}^T f_t^*, \tag{2}

该方程可以分解为两部分：(1) (\mathbf{F}^T \mathbf{F})^{-1}：Gram 矩阵的逆；(2) \mathbf{F}^T f_t^*：模型库 \mathbf{F} 中每个模型与超级模型 f_t^* 之间的成对相似性。理想情况下，这些相似性应均匀分布，确保 f_t^* 对 \mathbf{F} 中的任何单个模型保持无偏，从而实现多样化的长期知识自然融合。因此，我们可以将公式 (2) 简化为：

\mathbf{w} = (\mathbf{F}^T \mathbf{F})^{-1} \mathbb{1}^K. \tag{3}

接下来，计算 Gram 矩阵 \mathbf{G} = \mathbf{F}^T \mathbf{F}，它捕获了模型库 \mathbf{F} 中 任意两个模型 (f_i, f_j) 的参数相似性，如下所示：

\mathbf{G} = \mathbf{F}^T \mathbf{F} = \left( \langle f_i, f_j \rangle \right)_{i,j=1}^K \in \mathbb{R}^{K \times K}, \quad f_i, f_j \in \mathbf{F}, \tag{4}

其中 \langle f_i, f_j \rangle 表示模型参数 f_i 和 f_j 的内积。基于 \mathbf{G} 捕获的相似性，其逆矩阵 \mathbf{G}^{-1} 实际上优先考虑高方差的方向（多样化信息），并惩罚低方差的方向（重复信息）。

2.2.2 广义 Gram 矩阵的逆矩阵

（优化Gram逆矩阵） 虽然 Gram 矩阵的逆矩阵是有效的，但通过模型参数 f_i 和 f_j 的内积来评估相似性并不理想，因为具有不同参数的模型在相同的输入测试批次 x_t 上 可能会产生相似的预测。因此，为了针对每个输入批次 x_t 进行定制，我们比较了一对模型 (f_i, f_j) 的中间特征和最终边界框预测结果。为此，我们提出了 一个特征级相似性函数 S_{\text{feat}}(\cdot; \cdot) 和 一个输出级边界框集合相似性函数 S_{\text{box}}(\cdot; \cdot)，以有效量化任意两个 3D 检测模型之间的差异。

（优化公式3和4） 通过用提出的相似性函数替换内积，原始的 Gram 矩阵 \mathbf{G} 转变为一个专门设计用于 3D 检测器的广义版本 \widetilde{\mathbf{G}}。结合公式 (3) 和公式 (4)，我们可以计算 \widetilde{\mathbf{G}} 和最优协同权重 \widetilde{\mathbf{w}} 如下：

\widetilde{\mathbf{w}} = (\mathbf{F}^T \mathbf{F})^{-1} \mathbb{1}^K = \widetilde{\mathbf{G}}^{-1} \mathbb{1}^K, \quad \widetilde{\mathbf{G}} = \left( S_{\text{box}} \langle f_i, f_j \rangle \times S_{\text{feat}} \langle f_i, f_j \rangle \right)_{i,j=1}^K, \tag{5}

其中每个元素表示模型库 \mathbf{F} 中每对历史 3D 检测模型 (f_i, f_j) 的 特征和预测相似性。

（聚合得到超级模型） 超级模型 f_t^* 通过所有历史检查点 \mathbf{F} \in \mathbb{R}^K 加权线性聚合，权重为 \widetilde{\mathbf{w}} \in \mathbb{R}^K，如下所示：

f_t^* = \sum_{i=1}^K w_i f_i, \quad w_i \in \widetilde{\mathbf{w}}, \, f_i \in \mathbf{F}, \tag{6}

其中协同后的超级模型 f_t^* 用于指导当前模型 f_t 的监督。如图 4 （第2.1节中）所示，对于时间 t 的测试样本，组装后的 f_t^* 生成稳定的伪标签 \hat{\mathbf{B}}^t，并通过单次迭代训练 f_{t-1} \to f_t，如下所示：

\hat{\mathbf{B}}^t \gets f_t^*(x_t), \quad f_t \xleftarrow{\text{train}} \text{aug}(x_t, \hat{\mathbf{B}}^t), \tag{7}

其中 \text{aug}(\cdot, \cdot) 表示 应用于伪标签目标点云的数据增强操作。回顾公式 (5)，我们引入了一个特征级相似性函数 S_{\text{feat}}(\cdot; \cdot) 来评估 中间特征图 (\mathbf{z}_i, \mathbf{z}_j) 之间的独立性，并引入了一个输出级相似性函数 S_{\text{out}}(\cdot; \cdot) 来 衡量边界框预测 (\mathbf{B}^i, \mathbf{B}^j) 之间的差异，其中 (\mathbf{z}_i, \mathbf{z}_j) 和 (\mathbf{B}^i, \mathbf{B}^j) 由模型库 \mathbf{F} 中的任意一对模型 (f_i, f_j) 生成。

2.2.3 特征级相似性 S_{\text{feat}}

（利用秩评估） 为了评估特征图 (\mathbf{z}_i, \mathbf{z}_j) 之间的相似性，我们利用 特征矩阵的秩 来确定 \mathbf{z}_i 中的特征向量相对于 \mathbf{z}_j 中的特征向量之间的 线性依赖关系。特征图中的每个单个特征向量编码了 3D 场景中一个小 receptive field 的信息。在推断输入批次 x_t 时，如果 \mathbf{z}_i 中的一个特征向量与 \mathbf{z}_j 中的另一个特征向量线性独立，则意味着 \mathbf{z}_i 和 \mathbf{z}_j 要么捕获来自不同 receptive field 的信息，要么关注相同的区域但以不同的方式解释信息。

为了计算这些依赖关系，我们将 \mathbf{z}_i \oplus \mathbf{z}_j 进行拼接，并计算其秩 \text{rank}(\cdot)，该秩标识了线性独立特征向量的最大数量。\mathbf{z}_i \oplus \mathbf{z}_j 的秩越高，表示特征的多样性越大，因为较少的特征向量可以被其他向量线性组合。 为了加速计算，我们通过计算特征矩阵的核范数来近似 \text{rank}(\cdot) 。对于输入批次 x_t，检测模型对 (f_i, f_j) 之间的特征级相似性 S_{\text{feat}} 可以通过以下公式确定：

S_{\text{feat}} \langle f_i, f_j \rangle = 1 - \frac{\text{rank}(\mathbf{z}_i \oplus \mathbf{z}_j)}{D}, \quad \mathbf{z}_i, \mathbf{z}_j \in \mathbb{R}^{2HW \times D}, \tag{8}

其中 \mathbf{z}_i, \mathbf{z}_j 分别由 f_i 和 f_j 生成。H, W, D 表示特征图的高度、宽度和维度，而 D 是 \text{rank}(\cdot) 的最大可能值。S_{\text{feat}} 的取值范围为 0 到 1， S_{\text{feat}} 的值越高，表示 \mathbf{z}_i 和 \mathbf{z}_j 之间的特征独立性越低，从而导致由模型 f_i 和 f_j 生成的 特征图更相似。

2.2.4 输出级边界框相似性 S_{\text{box}}

（集合匹配问题） 为了评估边界框预测 (\mathbf{B}^i, \mathbf{B}^j) 之间的相似性，我们将其视为一个 集合匹配问题，因为 \mathbf{B}^i 和 \mathbf{B}^j 分别表示一组预测的边界框，其大小可能不同。为了解决这个问题，作者应用匈牙利匹配算法，这是一种用于二分图匹配的鲁棒方法，确保两组边界框预测之间达到最佳的一对一对应关系。我们将较小的边界框集合用 \emptyset 填充以使两组集合的大小相等为 N。为了确定这两个等大小集合之间的最优二分匹配，匈牙利算法被用来找到一个排列 p \in \mathbf{P}，使得成本最低：

\tilde{p} = \arg\min_{p \in \mathbf{P}} \sum_n \mathcal{L}_{\text{box}}(\mathbf{B}_n^i; \mathbf{B}_{p(n)}^j), \tag{9}

其中 \mathbf{B}_n^i 是模型 f_i 预测的集合 \mathbf{B}^i 中的第 n 个边界框。边界框损失 \mathcal{L}_{\text{box}}(\cdot; \cdot) 通过交并比（IoU）加上覆盖中心坐标、尺寸和方向角度的 L1 距离来计算，涉及一对边界框：\mathbf{B}_n^i 和由 p(n) 索引的相应边界框。指示函数 \mathbb{1}_{\{c_n^i \neq \emptyset\}} 表示仅当第 n 个对象的类别不是填充的 \emptyset 时才计算成本。下一步是计算所有匹配边界框对的总匈牙利损失：

S_{\text{box}}(f_i, f_j) = \left( \sum_{n=1}^N \mathbb{1}_{\{c_n^i \neq \emptyset\}} \mathcal{L}_{\text{box}}(\mathbf{B}_n^i; \mathbf{B}_{\tilde{p}(n)}^j) \right)^{-1}, \tag{10}

其中 \tilde{p} 是在公式 (9) 中计算出的最优分配。我们使用 sigmoid 函数将结果归一化到与 S_{\text{feat}} 相同的范围。S_{\text{box}} 的值越高，表示模型 f_i 和 f_j 预测的重叠边界框越多。

2.3 模型库更新

如图 4 所示，在适应每 L 个样本 \{x_l, x_{l+1}, \cdots, x_L\} 时，单个检查点 f_i \in \mathbf{F} 参与 L 次组装，从而计算并存储一组协同权重 \{w(l,i), w(l+1,i), \cdots, w(L,i)\}。给定 \mathbf{F} 中的 K 个检查点，定义协同矩阵为 \mathbf{W} = (w(l,k))_{l=1,k=1}^{L,K} \in \mathbb{R}^{L \times K}。在推断完 L 个批次后，我们在 L 维度上取平均值，计算每个检查点的 平均协同权重，表示为：

\bar{\mathbf{w}} = \{\bar{w}_1, \cdots, \bar{w}_K\} \in \mathbb{R}^K. \tag{11}

最后，我们 移除平均协同权重最低的模型，并将当前模型 f_t 添加到模型库中，如下所示：

\mathbf{F} \leftarrow \mathbf{F} \setminus \{f_i\}, \quad i = \text{index}(\bar{\mathbf{w}}; \min(\bar{\mathbf{w}})), \quad \mathbf{F} \leftarrow \mathbf{F} \cup \{f_t\}, \tag{12}

其中 i 表示 \bar{\mathbf{w}} 中最小平均协同权重的索引。

3 实验

跨数据集偏移

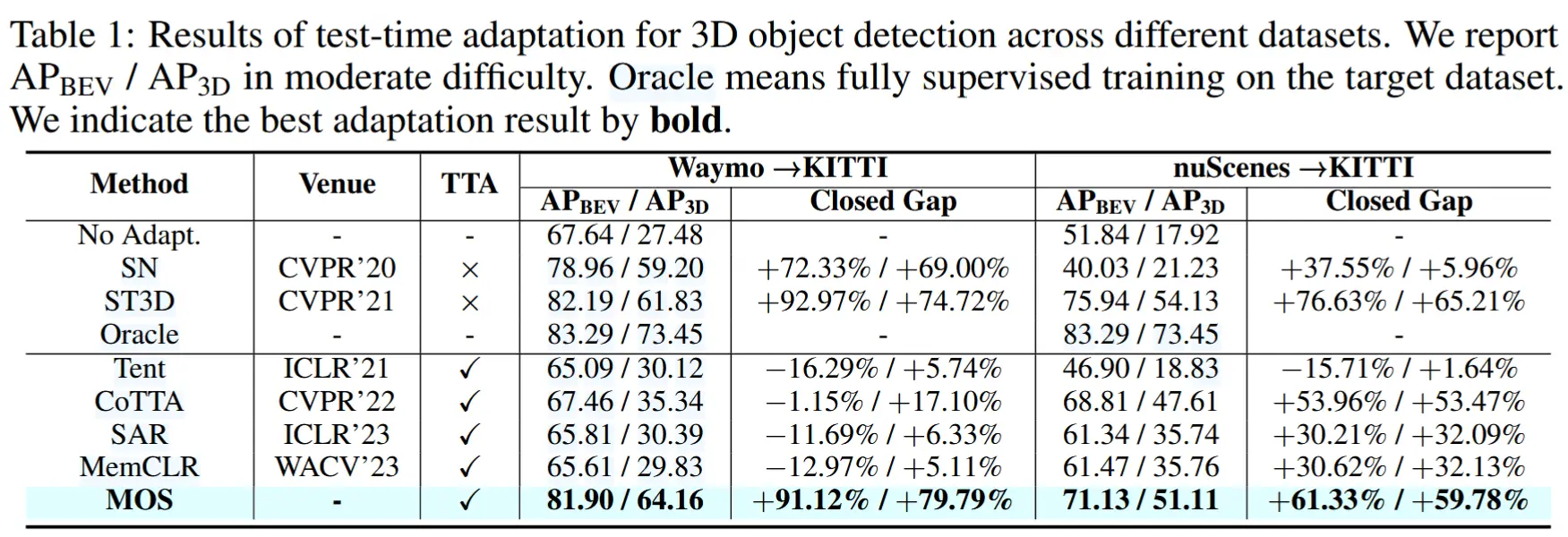
损坏偏移

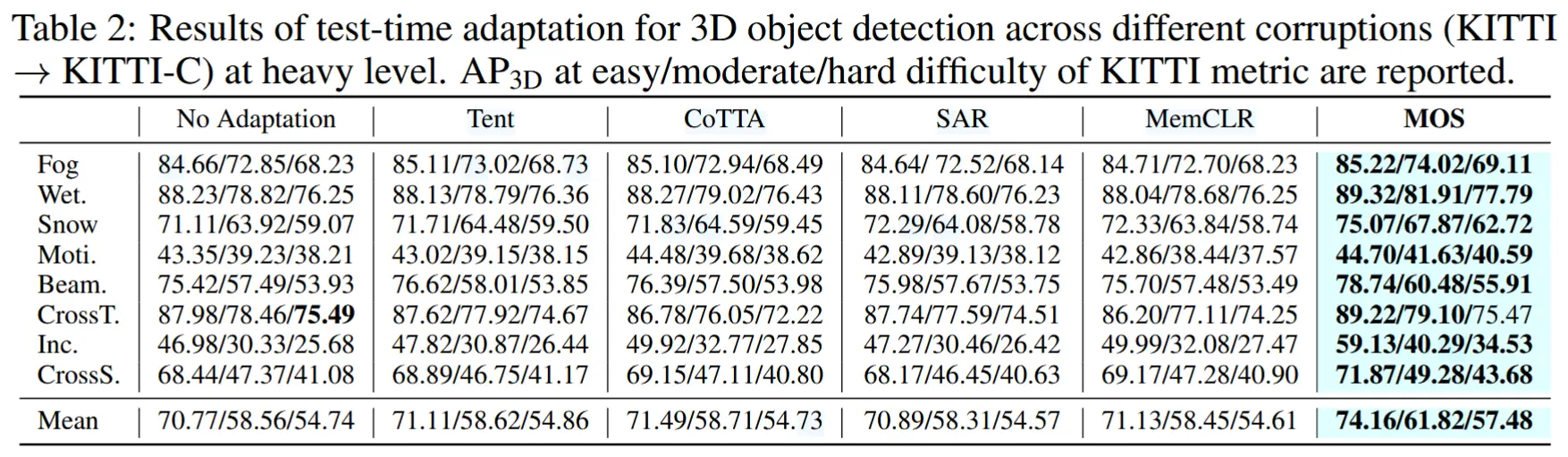
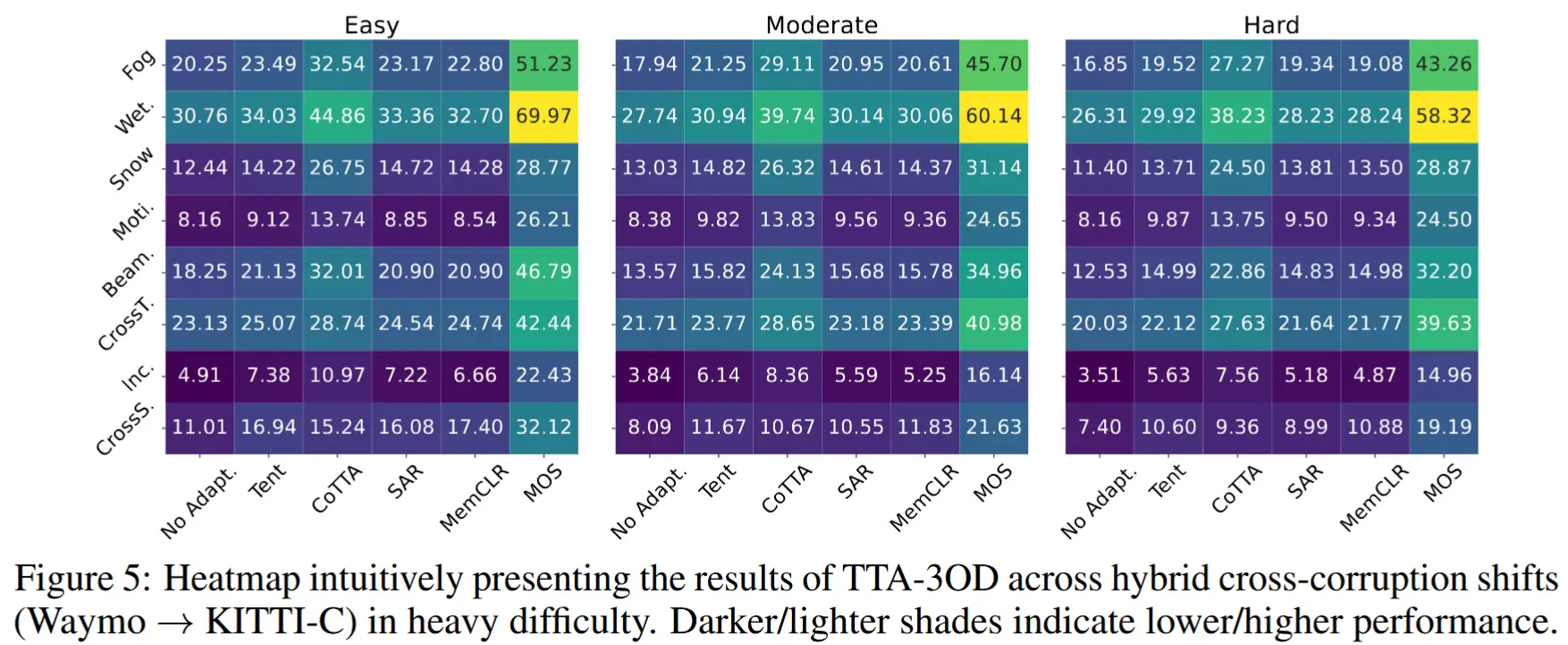
跨损坏偏移 Crpss-corruption

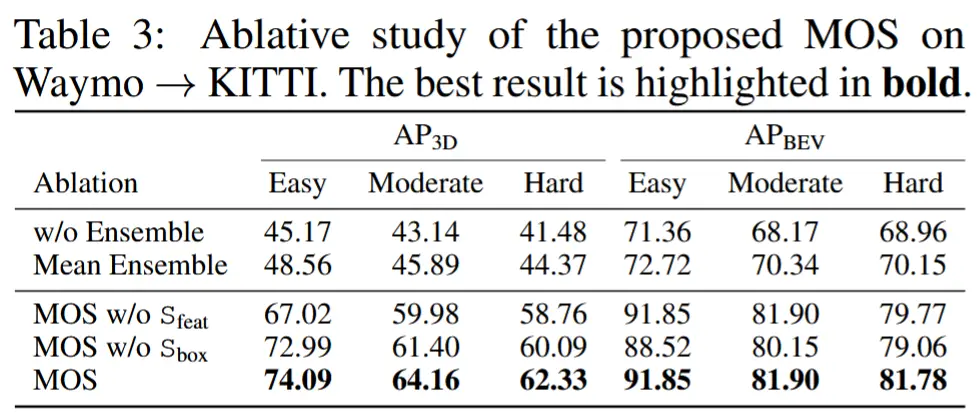
消融

论文笔记《MOS: MODEL SYNERGY FOR TEST-TIME ADAPTATION ON LIDAR-BASED 3D OBJECT DETECTION》

摘要