论文 - 《Towards Robust Multimodal Open-set Test-time Adaptation via Adaptive Entropy-aware Optimization》
代码 - Github
关键词 - 开放集、TTA、多模态、熵、LiDAR

摘要

研究问题
- TTA：测试时自适应，应对训练数据与测试数据之间的分布偏移。
- OSTTA：开放集测试时自适应，将一个在源域上预训练的模型在线适应到一个包含未知类别的无标签目标域中。
现有不足
- 现有方法主要聚焦于单模态的 OSTTA，通常仅通过过滤低置信度样本来应对未知类问题，而未能有效处理多模态数据的复杂性。
观察
- 目标域中已知类与未知类样本之间的熵差异与多模态开放集测试时自适应（MM-OSTTA）的性能强相关。
本文方法
- 提出了专为 MM-OSTTA 设计的全新框架 — 自适应熵感知优化（Adaptive Entropy-aware Optimization, AEO）。
- 两个关键组件：
  - 未知感知的自适应熵优化（Unknown-aware Adaptive Entropy Optimization, UAE）
  - 自适应模态预测差异优化（Adaptive Modality Prediction Discrepancy Optimization, AMP）
- 这两个组件通过 增强已知与未知类别样本之间的熵差异 ，有效提升模型在在线适应过程中的未知类别识别能力。
实验
- 搭建了一个新的基准测试集，包含两个任务：动作识别（视频、音频和光流）和三维语义分割（LiDAR 和相机图像）。
- 大量实验证明了 AEO 框架的有效性、广泛适应能力、稳健性。

1 引言

MM-OSTTA
- 目标：将一个预训练的多模态模型从源域自适应到一个全新的目标域，该目标域保留了相同的模态信息，但包含了未知类别样本。
- 关键挑战：如何有效地利用不同模态之间的互补信息，以提升自适应能力与未知类别的检测效果，而当前的单模态开放集 TTA 方法在这方面显得力不从心。
AEO
- 观察：目标域中已知与未知样本之间熵差越大，未知类别的检测性能越好。
- AEO框架目标：在在线适应过程中 放大已知与未知样本之间的熵差异 。
- 两个组件
  - UAE 基于熵阈值动态地为每个样本分配权重，并自动判断该样本应进行熵最小化还是最大化；
  - AMP 则在模态之间自适应地调整预测差异，对于未知样本鼓励各模态之间生成多样的预测结果，而对于已知样本则保持一致性。

2 MM-OSTTA 问题定义

MM-OSTTA 旨在将一个预训练的源模型适应到目标域，该目标域在多个模态中同时经历 分布偏移（distribution shifts）和标签偏移（label shifts）。

（源域 & 目标域） 令 \mathcal{D}_S = \{(x_i, y_i)\}_{i=1}^{N_S} 表示源域数据集，其标签空间为 \mathcal{C}_S，遵循分布 P_{\mathcal{X}\mathcal{Y}}^S，其中每个样本 x_i 包含 M 个模态，表示为 x_i = \{x_i^k \mid k = 1, \cdots, M\}。类似地，令 \mathcal{D}_T = \{(x_i, y_i)\}_{i=1}^{N_T} 表示目标域数据集，其标签空间为 \mathcal{C}_T，遵循分布 P_{\mathcal{X}\mathcal{Y}}^T。

（模型结构） 令 f: \mathcal{X} \mapsto \mathbb{R}^C 表示在源分布 P_{\mathcal{X}\mathcal{Y}}^S 上训练的神经网络，其中 C 是 \mathcal{C}_S 中的类别数。在 MM-OSTTA 中，f 由 M 个特征提取器 g_k(\cdot) 和一个分类器 h(\cdot) 组成。每个特征提取器 g_k(\cdot) 处理模态 k，生成嵌入 \mathbf{Z}^k，而分类器 h(\cdot) 将这些嵌入组合起来生成预测概率 \hat{p}：

\hat{p} = \delta(f(\mathbf{x})) = \delta(h([g_1(x^1), \ldots, g_M(x^M)])) = \delta(h([\mathbf{Z}^1, \ldots, \mathbf{Z}^M])), \tag{1}

其中 \delta(\cdot) 表示 softmax 函数。此外，我们为每个模态 k 包含单独的分类器 h_k(\cdot)，从而生成 模态特定的预测概率 \hat{p}^k = \delta(h_k(g_k(x^k)))。

给定在源数据集 \mathcal{D}_S 上训练好的多模态源模型 f(\mathbf{x})，MM-OSTTA 的目标是将该模型适应到目标域 \mathcal{D}_T，其中 P_{\mathcal{X}\mathcal{Y}}^S \neq P_{\mathcal{X}\mathcal{Y}}^T。与传统的闭集测试时适应（closed-set TTA）不同，后者假设 \mathcal{C}_S = \mathcal{C}_T，MM-OSTTA 在条件 \mathcal{C}_S \subseteq \mathcal{C}_T 下运行，这意味着目标域可能包含源域中不存在的未知类别的样本。

（预测得分） 除了模型适应和预测外，MM-OSTTA 还涉及 为每个样本生成预测得分 S(\mathbf{x})，并使用 未知类检测器 G_\eta(x)，定义如下：

G_\eta(x) = \begin{cases} \text{known} & S(\mathbf{x}) \geq \eta \\ \text{unknown} & S(\mathbf{x}) < \eta \end{cases}, \tag{2}

其中 \eta 是预定义的阈值。满足 S(\mathbf{x}) < \eta 的样本被分类为未知类。默认情况下，使用 Maximum Softmax Probability （MSP）作为 S(\mathbf{x})。

3 方法论

3.1 熵与 MM-OSTTA 性能的相关性

（指标定义） 预测熵定义为 H(\hat{p}) = - \sum_{c} \hat{p}_c \log \hat{p}_c 、已知样本的平均预测熵 H_{\text{known}} 、未知样本的平均预测熵 H_{\text{unknown}}。

（实验设计） 使用在源域上预训练的模型，我们对目标域进行预测，且不进行任何适应。计算已知和未知样本的差值，EPIC-Kitchens 数据集，在不同的领域偏移场景下评估这个熵差异，并分析它与 MM-OSTTA 性能指标（FPR95）之间的相关性，FPR95 测量的是未知类别检测能力，FPR95 越低表示性能越好。

（结果/观察） 如图 2 所示，熵差异与 MM-OSTTA 性能之间存在强相关性，较大的熵差异对应较低的 FPR95。较高的熵差异表明，未知样本的熵明显大于已知样本，从而使得它们更容易区分。

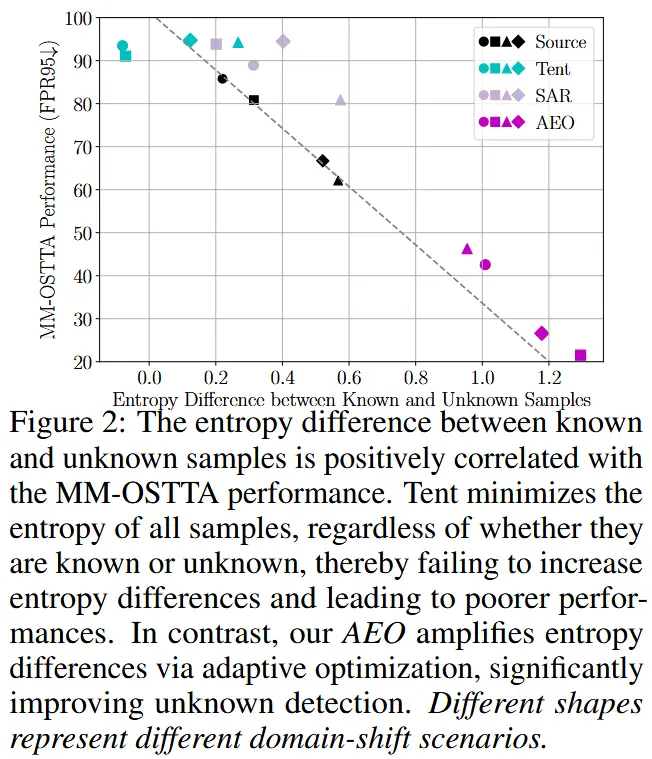
Tent 方法最小化所有样本的熵，无论它们是属于已知类别还是未知类别，这会无意中减少这些类别之间的熵差异，这种熵差异的减小导致了性能下降。

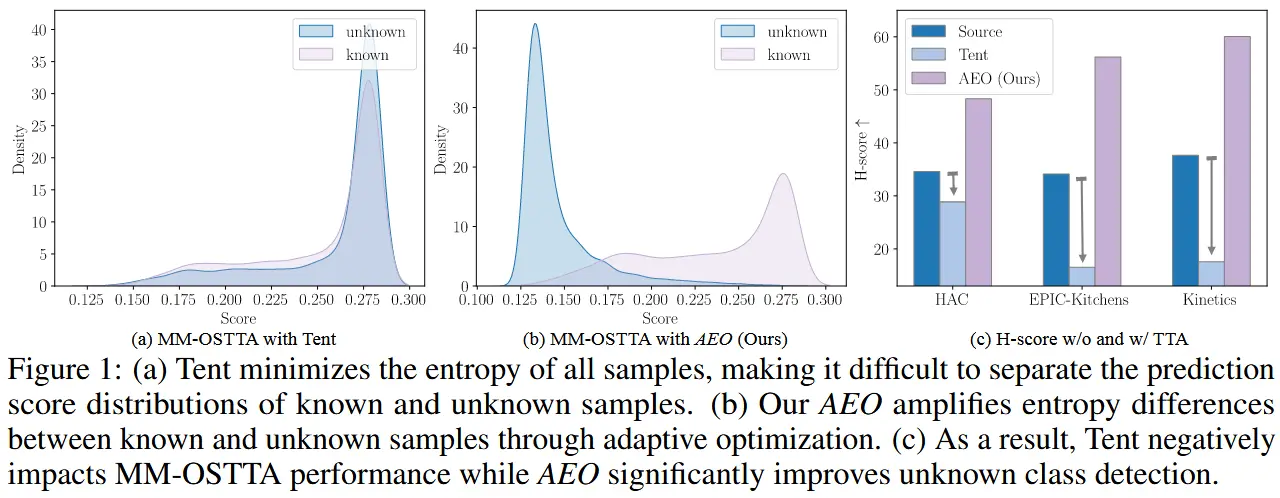
3.2 未知感知的自适应熵优化 UAE

（解决思路） 有效优化已知类和未知类样本熵的第一步是可靠地识别潜在的未知类样本。

（UAE介绍） 为了解决这一问题，我们引入了 未知感知自适应熵优化损失，该损失根据每个样本的预测不确定性自适应地加权并优化样本。UAE 损失定义如下：

W_{ada} = \text{Tanh}(\beta \cdot (H(\hat{p}) - \alpha)), \tag{3}

\mathcal{L}_{AdaEnt} = -H(\hat{p}) \cdot W_{ada}, \tag{4}

其中，\text{Tanh} 是双曲正切函数，W_{ada} 是分配给每个样本的自适应权重，H(\hat{p}) 是预测概率 \hat{p} 的归一化熵，即 H(\hat{p}) = -\left(\sum_c \hat{p}_c \log \hat{p}_c\right) / \log(C)，其中 C 表示类别数。参数 \alpha 和 \beta 分别控制熵的阈值和缩放。

（Tanh(x)分类讨论） 函数 \text{Tanh}(x) 在 x > 0 时为正，在 x < 0 时为负

在 H(\hat{p}) > \alpha（即预测置信度较低，表明样本可能是未知类）时 最大化 H(\hat{p})
在 H(\hat{p}) < \alpha（即预测置信度较高，表明样本可能是已知类）时 最小化 H(\hat{p})。
在 H(\hat{p}) << \alpha 或者 H(\hat{p}) >> \alpha 时， \text{Tanh}(x) 渐近接近 +1/-1，从而对那些最可能是已知类或未知类的样本 赋予更高的权重。
当 H(\hat{p}) 接近 \alpha 时，模型对样本是已知类还是未知类存在不确定性，此时错误预测的风险更高。在这种情况下，分配的权重接近 0，有效地中和了不确定样本的潜在负面影响。

通过这种方式， UAE 损失自适应地优化每个样本的熵，增强已知类和未知类样本之间的分离，从而确保更可靠的预测。

3.3 自适应模态预测差异优化

（AMP介绍） 为了进一步增强已知类和未知类样本之间的熵差，我们引入了 自适应模态预测差异优化，该方法 优化不同模态之间的预测。

（\mathcal{L}_{AdaEnt*}） 当置信度较低时增加每个模态的预测熵，而当置信度较高时减少预测熵。 损失定义如下：

\mathcal{L}_{AdaEnt*} = -\frac{1}{2}(H(\hat{p}^1) + H(\hat{p}^2)) \cdot W_{ada}, \tag{5}

其中 W_{ada} 是根据公式 (3) 计算的自适应权重。

（\mathcal{L}_{AdaDis}） 对于未知样本，最大化其在不同模态之间的预测差异，鼓励不确定性，即跨模态多样化预测会增加最终预测的不确定性；对于已知样本，强制在不同模态之间 保持一致性，以确保预测的置信度，即高置信度的预测应在所有模态中表现出一致的输出。为实现这一点，定义自适应模态预测差异损失为：

\mathcal{L}_{AdaDis} = -(Dis(\hat{p}^1, \hat{p}^2)) \cdot W_{ada}, \tag{6}

其中 W_{ada} 是公式 (3) 中的自适应权重，\mathcal{L}_{AdaDis} 强调具有极高或极低 H(\hat{p}) 的样本。Dis(\cdot) 测量两个模态之间的预测差异，其默认选择是 L_1 距离。如图 3 所示，使用 AMP 进行训练进一步增加了熵差，从而提升了性能。

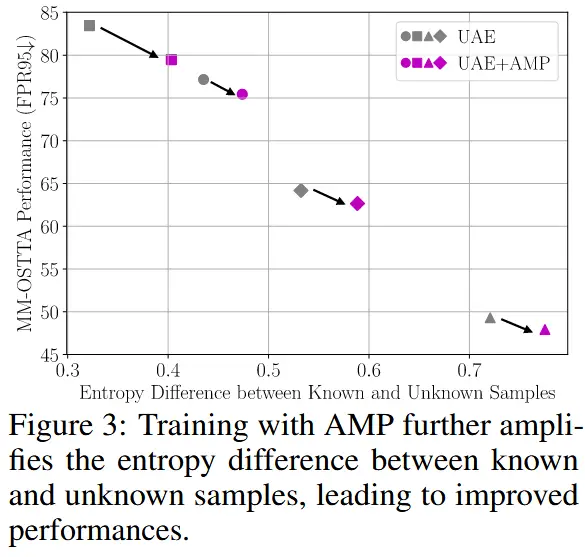
（\mathcal{L}_{Div}）作者还引入了一个负熵损失项 \mathcal{L}_{Div}，以确保预测的多样性：

\mathcal{L}_{Div} = \sum_{c=1}^{C} p_c \log p_c, \tag{7}

其中 p_c 是一个批次中类别 c 的累积预测概率。

（总损失函数） 最终损失计算为之前定义的损失的加权和：

\mathcal{L}_{AEO} = \mathcal{L}_{AdaEnt} + \gamma_1 (\mathcal{L}_{AdaEnt*} + \mathcal{L}_{AdaDis}) + \gamma_2 \mathcal{L}_{Div}. \tag{8}

注意，总共有四个损失函数，通过加权求和得到最终的损失函数。

4 实验

4.1 实验设置

数据集
- 领域适应实验
  - EPIC-Kitchens： 包含八个动作，在三个不同的厨房中录制。
  - HAC： 包含七个动作，由人类（H）、动物（A）和卡通（C）角色执行。
  - 两者均提供三种模态：视频、音频和光流。将 HAC 样本视为 EPIC-Kitchens 的未知类别，反之亦然。
- 腐蚀鲁棒性实验
  - Kinetics-100-C、HAC-C，分别对音频和视频做六种腐败偏移，腐蚀级别5。
  - 在开放集设置中，我们将 HAC 作为未知类别，并应用与 Kinetics-100-C 相同的腐蚀类型，生成 HAC-C 数据集。
- 多模态三维语义分割实验
  - nuScenes 数据集：包括 LiDAR 和摄像头模态。
  - 适应场景：Day-to-Night 适应、USA-Singapore 适应。
评估指标
- 在已知数据上的适应能力，使用 分类任务的准确率Acc 和 分割任务的交并比IoU。
- 在未知类别上的鲁棒性，使用 AUROC 和 假阳性率FPR95。
- H-score：
  
  H\text{-score} = \frac{3}{\frac{1}{\text{Acc}} + \frac{1}{\text{AUROC}} + \frac{1}{1 - \text{FPR95}}} \tag{9}
基线：Tent SAR OSTTA UniEnt READ

4.2 SOTA对比

领域适应鲁棒性
- 评估提出的 AEO 方法在多模态开放集 TTA 设置下的性能。
- 在 EPIC-Kitchens 数据集上，使用视频和音频模态进行训练和适应。在 HAC 数据集熵，使用多种模态组合进行训练和适应。
- 如表1和表2，AEO 框架在 EPIC-Kitchens 和 HAC 数据集上均表现出色，显著提升了 H-score 和 FPR95 等指标。

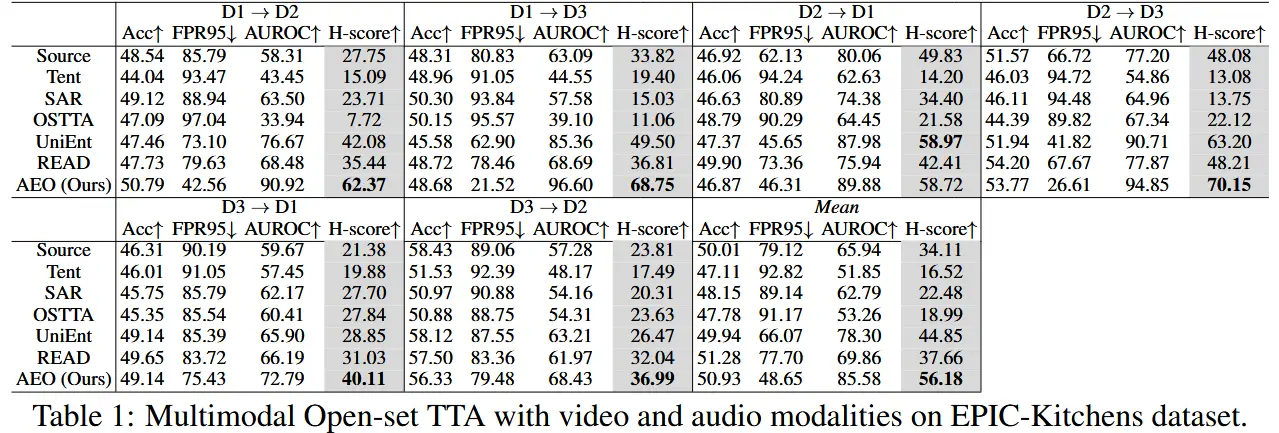
腐蚀鲁棒性
- 在 Kinetics-100-C 数据集上评估 AEO 方法在视频和音频模态腐蚀下的适应能力。
- 如表3所示，AEO 在各种腐蚀类型下表现优异，相比源模型，H-score 提高了 32.78% 和 26.50%。

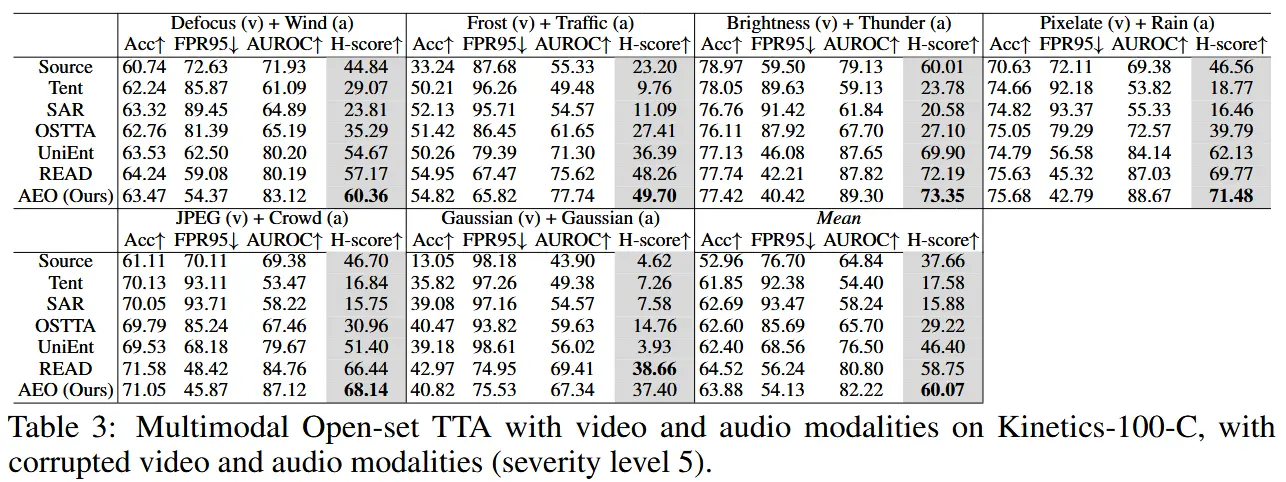
长期 MM-OSTTA
- 模拟 10 轮适应过程，评估在长时间适应中的性能变化。
- 如表4所示，在模拟长期适应的 10 轮实验中，AEO 显示了 7.67% 的 H-score 改进，表明其在长时间适应中有效应对错误积累。

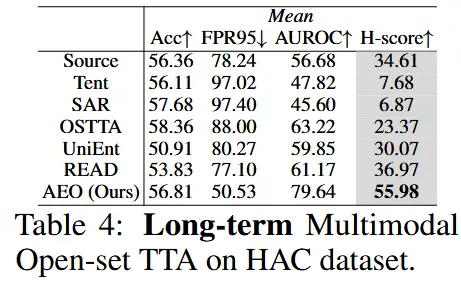
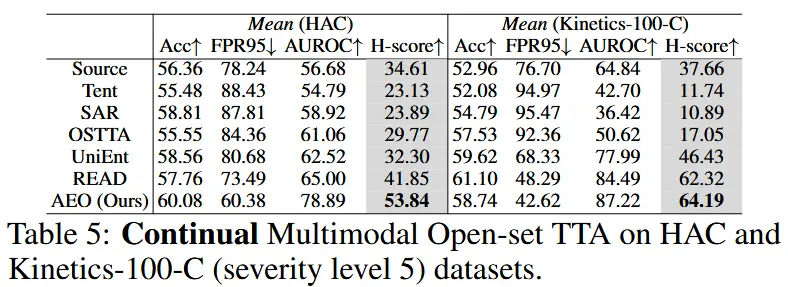
持续 MM-OSTTA
- 在 HAC 数据集和 Kinetics-100-C 数据集上，模拟领域连续变化（如 H → A → C），评估方法的持续适应能力。
- 如表5，在持续适应实验中，AEO 保持了强大的表现，相比基准方法，H-score 显著提高。

分割任务扩展性
- 在 nuScenes 数据集上，进行三维语义分割任务，使用 LiDAR 和摄像头模态进行训练和测试。
- 在三维语义分割任务中，AEO 显著提高了 FPR95，比源模型高出 8.22%，证明了 AEO 方法在不同任务和模态中的有效性。

除了上述实验，作者还做了以下实验，在此不一一展示。

Ablation on each proposed module.

Ablation on hyperparameters in W_{ada}.

Applicability on different architectures.

Robustness to different pre-trained models.

Prediction score distributions before and after TTA.

Different ratios of unknown samples.

Robustness under mixed distribution shifts.

论文笔记《Towards Robust Multimodal Open-set TTA via Adaptive Entropy-aware Optimization》

摘要