论文 - 《Attention Bootstrapping for Multi-Modal Test-Time Adaptation》
关键词 - 多模态（视频+音频）、TTA、主成分熵最小化

摘要

问题背景：测试时间自适应（Test-time adaptation）以往的研究主要集中在单一模态上，但在多模态场景下，测试时间分布偏移更为复杂，需要新的解决方案。
动机：作者观察到了一种名为注意力差距的现象。即测试时间分布偏移会导致模态间的对齐错位，从而在 单模态差异（通过自注意力衡量） 和 跨模态差异（通过交叉注意力衡量） 之间产生显著差距。随着分布偏移的加剧，这种注意力差距会进一步扩大，阻碍有效的模态融合。
本文工作 - 基于注意力引导与主成分熵最小化的自适应方法（Attention Bootstrapping with Principal Entropy Minimization, ABPEM）
- 提出了注意力引导（attention bootstrapping） 方法，该方法利用自注意力指导交叉注意力的优化。
- 此外，为了减少常用熵最小化方法中的梯度噪声，我们采用了主成分熵最小化（principal entropy minimization） 。通过聚焦于熵的主要部分，排除不可靠的梯度信息，从而有效降低梯度噪声。

1 介绍

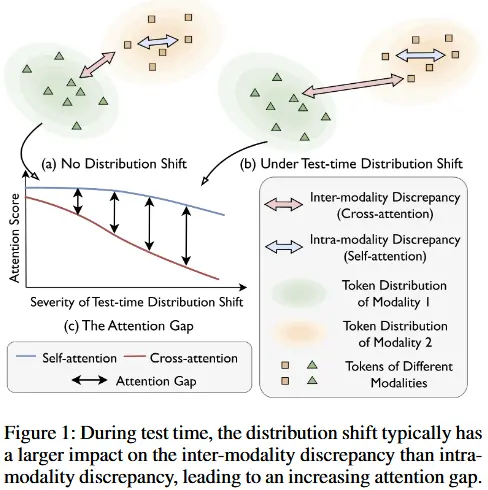
注意力差距
- 如图 1 所示，测试时间分布偏移不仅导致单模态内的变化（蓝色箭头），还引发跨模态的变化（红色箭头），后者可能会削弱模型有效对齐和融合不同模态的能力，因为分布偏移下交叉注意力往往会减弱。
- 如图 1 所示，当基于注意力的模型面临测试时间分布偏移时，单模态内的差异（intra-modality discrepancies）仅略微增加，而跨模态差异（inter-modality discrepancies）显著增加，从而导致了 注意力差距（attention gap）。

基于注意力引导与主成分熵最小化的自适应方法 ABPEM
- 注意力引导
  - 目标：增强交叉注意力并减少跨模态差异。
  - 利用自注意力得分来提升交叉注意力得分。
  - 具体而言，对原始交叉/自注意力得分的分布进行建模，并使用自注意力得分的分布作为锚点，来对齐交叉注意力得分的分布。这种方法优于简单的差异最小化方法，因为它考虑了每个模态的内在可靠性。
  - 可以想象，当分布偏移导致单模态内差异增大时（表现为低自注意力得分），该模态的可靠性会降低。在这种情况下，我们会得到一个较低的锚点（低自注意力得分），从而使得交叉注意力得分的目标值也较低，进而减少对该模态的关注。
- 主成分熵最小化
  - 目标：减少多模态测试时间自适应中的自监督信号噪声。
  - 在测试时间分布偏移的情况下，模型对低概率类别的预测变得不太可靠，其梯度也会引入噪声。因此，所提出的主成分熵最小化方法排除了低概率类别，仅关注高概率（主要）类别，从而减少了梯度噪声。

2 相关工作

2.1 TTA

相关工作
- 熵最小化：利用模型预测的不确定性进行优化。
- 样本选择：通过选择可靠样本提高模型性能。
- 归一化层调优：调整模型的归一化层以适应分布偏移。
- 表示不变性：增强模型对分布变化的鲁棒性。
- 自监督学习：通过无监督任务提升模型泛化能力。
- 生成方法：利用生成模型处理分布偏移。
- 局限：单模态场景。
类似工作
- Shin 等人（Shin et al. 2022）专注于特定任务（2D-3D 联合分割），而本文方法适用于更通用的多模态场景。
- Yang 等人（Yang et al. 2024）揭示了多模态分布偏移引起的可靠性偏差问题，并提出了 READ 方法来解决可靠性问题。
- 相比之下，本文观察到一种阻碍模态融合的不同现象——注意力差距（attention gap），并提出了 ABPEM 方法，以在分布偏移下促进模态融合。

2.2 多模态学习

从多模态数据中学习是深度学习的重要课题。近年来，越来越多的研究关注不同模态的对齐和融合。研究人员致力于在不利条件下确保有效融合，包括以下场景：
- 模态不平衡 （Modality Imbalance）：某些模态的数据量或质量不足。
- 缺失模态 （Missing Modality）：部分模态数据不可用。
- 分布偏移 （Distribution Shift）：训练和测试数据分布不一致。
局限：这些研究主要集中在模型的训练阶段，在资源受限的情况下，调整模型的主干网络可能不可行。此外，这些算法通常需要数据的标签信息，而这些标签在实际应用中往往难以获取。

3 方法论

3.1 问题定义

音频，记为 A ；视频，记为 V 。每种模态的输入分别表示为 x^A 和 x^V 。多模态学习系统通过特定于模态的编码器 \mathcal{E}^A 和 \mathcal{E}^V ，将输入编码到隐藏空间中的两组 token 中，即 \{z_i^A\}_{i=1}^{T_A} 和 \{z_i^V\}_{i=1}^{T_V} （其中 T_A 和 T_V 分别是 token 的数量）。然后，一个基于注意力的融合模块 \mathcal{F} 被用于结合这两组 token 并输出概率分布，即 p = \mathcal{F}(\{z_i^A\}_{i=1}^{T_A}, \{z_i^V\}_{i=1}^{T_V}) 。概率分布表示为 p = [p_1, \cdots, p_C] \in \Delta^{C-1} ，其中 C 是类别的数量， \Delta^{C-1} 是概率单纯形。

在多模态测试时间自适应中，模型 M = (\mathcal{E}^A, \mathcal{E}^V, \mathcal{F}) 已经在训练集 \mathcal{D}_{tr} = \{(x_i^A, x_i^V, y_i)\}_{i=1}^{N_{tr}} 上进行了训练，其中 N_{tr} 是训练集的大小， y_i 是标签。然而，任务不假设可以访问训练集 \mathcal{D}_{tr} ，而是目标是利用无标签的测试数据 \mathcal{D}_{te} = \{(x_i^A, x_i^V)\}_{i=1}^{N_{te}} 来提升模型性能，其中 N_{te} 是测试集的大小。为了实用性，我们固定 \mathcal{E}^A 和 \mathcal{E}^V ，仅调整 \mathcal{F} 中的一小部分参数。

3.2 框架描述

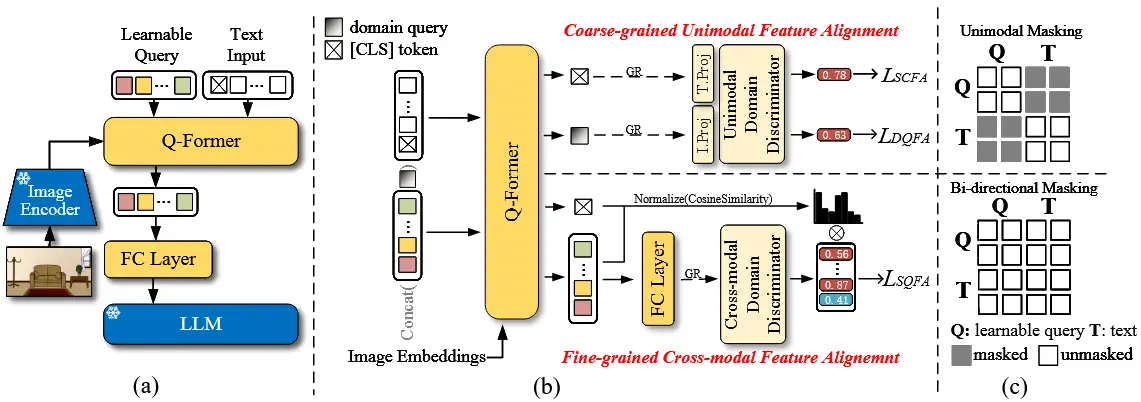
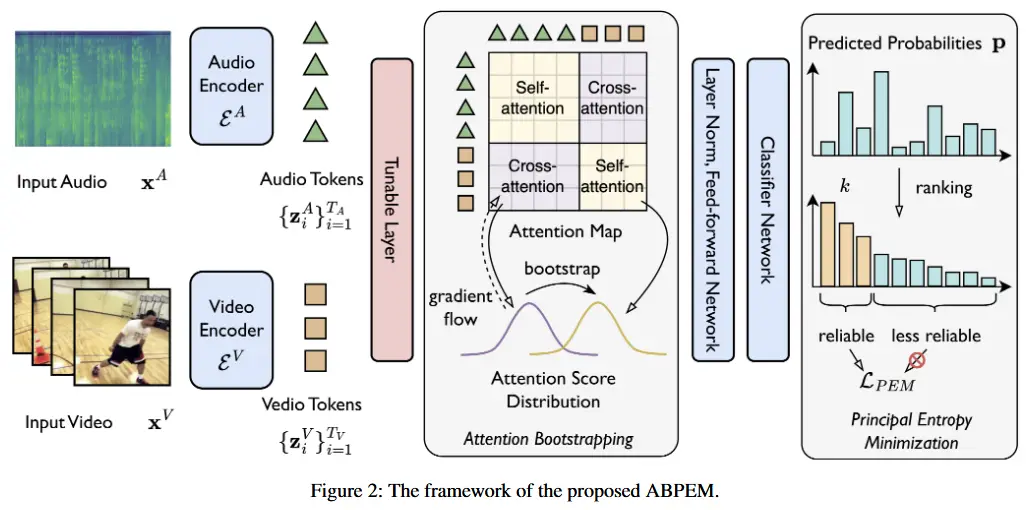
所提出的 ABPEM 框架如图 2 所示。

输入的音频和视频分别由 \mathcal{E}^A 和 \mathcal{E}^B 编码以获得隐藏空间表示（即 token）。
然后，来自不同模态的 token 被拼接起来，并应用可调层生成每个 token 的查询、键和值，这些用于注意力机制。注意力引导被应用于注意力图，以对齐交叉注意力和自注意力的分布。
随后，经过注意力处理的 token 经过层归一化、前馈网络和分类器网络，生成预测概率 p \in \Delta^{C-1} 。
最后，主成分熵最小化选取最可靠的前 k 类，并计算熵的主要部分，这是目标的一部分。

3.3 注意力引导

（注意力机制）

在上述范式下，由模态特定编码器学习到的 token 首先被拼接为 Z = [z_1^A, \dots, z_{T_A}^A, z_1^V, \dots, z_{T_V}^V]^T 。随后，Q, K, V 的计算公式如下：

Q = Z W_Q + B_Q, \quad K = Z W_K + B_K, \\ \quad V = Z W_V + B_V, \tag{1}

其中，W_{Q,K,V} 和 B_{Q,K,V} 是 测试时可学习的参数。然后，可以使用查询和键来计算未归一化的注意力：

\widetilde{A} = Q K^T. \tag{2}

我们将 \widetilde{A} 分解为四个部分，即：

\widetilde{A} = \begin{bmatrix} \widetilde{A}^{A2A} & \widetilde{A}^{A2V} \\ \widetilde{A}^{V2A} & \widetilde{A}^{V2V} \end{bmatrix}, \tag{3}

其中，上标 X2Y 表示当模态 X 作为查询而模态 Y 作为键时的未归一化注意力。归一化的注意力分数用于融合不同模态：

A = \text{softmax}(\widetilde{A}/\sqrt{d}), \quad Z' = A V, \tag{4}

其中， d 是 token 的维度， Z' 是经过注意力处理后的 token 嵌入。

（建模模态内和跨模态差异）

当模型遇到测试时间分布偏移时，可能会发生模态不匹配，从而导致单模态内差异和跨模态差异。例如，当输入视频受到分布偏移的影响时，由于不确定性增加（单模态内差异），token 嵌入的分布 \{z_i^V\}_{i=1}^{T_V} 将会有略微更高的方差，并且它们也会偏离音频 token 的分布（跨模态差异）。

单模态内差异通过自注意力分数 \widetilde{A}^{V2V} 的减少值来体现，而跨模态差异则通过交叉注意力 \widetilde{A}^{A2V} 的减少值来体现。需要注意的是，我们 使用未归一化的注意力分数（即 softmax 之前的值），因为它们更好地反映了分布的距离。归一化的注意力分数会受到许多因素的影响（例如 token 的数量）。为了更好地描述注意力分数，我们将它们建模为 高斯分布：

P_{A2A}(a) \sim \mathcal{N}(\mu_{A2A}; \sigma_{A2A}^2), \\ \mu_{A2A} = \text{avg}(\widetilde{A}_{ij}^{A2A}), \quad \sigma_{A2A}^2 = \text{var}(\widetilde{A}_{ij}^{A2A}), \tag{5}

其中， i = 1, 2, \cdots, T_A 和 j = 1, 2, \cdots, T_A 。类似地，P_{A2V}(a) ， P_{V2V}(a) ，和 P_{V2A}(a) 可以被定义。

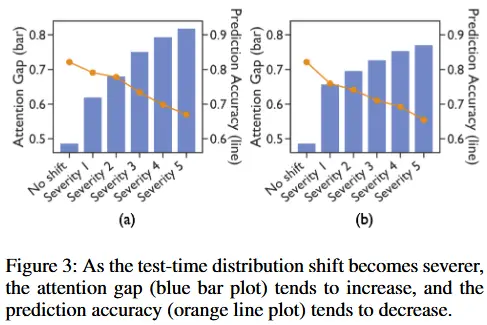
在图 3 中，我们提供了注意力差距存在且随着测试时间分布偏移加剧而增大的实证证据。具体来说，引入了两种类型的噪声，并测量注意力差距 \mu_{V2V} - \mu_{A2V} 以及模型的预测精度。如图所示，当模型面临测试时间分布偏移时，注意力差距（蓝色条形图）通常会增加，而预测精度（橙色折线图）则下降。这表明，在分布偏移的情况下，跨模态依赖性（由交叉注意力分数 P_{A2V}(a) 和 P_{V2A}(a) 表示）比单模态依赖性（由自注意力分数 P_{A2A}(a) 和 P_{V2V}(a) 表示）受到的影响更大。

（引导缩小差距）

因此，一个可行的解决方案是进行 注意力引导，利用自注意力分数作为锚点来提升交叉注意力分数，从而减少注意力差距，促进模态融合。

具体而言，我们采用最小化注意力分数分布之间的 KL 散度的策略，其公式如下：

\mathcal{D}_{KL}(P_{A2V} \| P_{V2V}) = \log \frac{\sigma_{V2V}}{\sigma_{A2V}} - \frac{1}{2} \\ + \frac{\sigma_{A2V}^2 + (\mu_{A2V} - \mu_{V2V})^2}{2\sigma_{V2V}^2}. \tag{6}

在公式 (6) 中，P_{V2V} 反映了视频模态如何关注自身，而 P_{A2V} 描述了音频模态如何关注视频模态。换句话说， P_{V2V} 反映了视频的自我评估： \mu_{V2V} 是对与预测任务相关的信息量的评估，而 \sigma_{V2V} 是对 token 间的可区分性的评估。当视频模态本身已经完全适应了分布偏移时，这种评估可能比音频模态的评估（ \mu_{A2V} 和 \sigma_{A2V} ）更好，因为存在模态差异。因此，我们的目标是减少跨模态差异，使它们类似于单模态差异（但不降至零，因为我们希望保留不同 token 的自然差异）。因此，使用 P_{V2V} 作为锚点来引导 P_{A2V} 是合理的。我们将自注意力分数 \mu_{V2V} 和 \sigma_{V2V} 的梯度流停止，以避免影响锚点。

类似地，可以计算 \mathcal{D}_{KL}(P_{V2A} \| P_{A2A}) ，注意力引导的损失目标函数可以表示为：

\mathcal{L}_{AB} = \mathcal{D}_{KL}(P_{A2V} \| P_{V2V}) + \mathcal{D}_{KL}(P_{V2A} \| P_{A2A}). \tag{7}

3.4 主成分熵最小化

在这部分，作者引入了主成分熵最小化，从类别角度解决这一问题。具体来说，我们可以将 p 的熵写为：

\mathcal{H}(p) = -\sum_{i \in \mathcal{S}} p_i \log p_i, \tag{8}

其中， \mathcal{S} = \{1, 2, \cdots, C\} 是所有类别的集合。

然而，公式 (8) 包含了所有类别的项，包括更可靠的类别和不太可靠的类别。我们将每个类别的排名记为 r_i ， i \in \mathcal{S} ，其形式定义如下：

r_i = |\{p_j \mid j \in \mathcal{S} \land p_j \geq p_i\}|, \tag{9}

其中 |\cdot| 表示集合的基数。我们的观察表明，排名较低的类别（即概率较高的类别）对测试时间分布偏移更具鲁棒性。因此，在熵的计算中排除不太可靠的类别是合理的。

具体来说，我们基于预测概率 p_i 得到的排名 r_i ，为每个测试样本定义可靠类别集合 \mathcal{S}_R^{(k)} ，其定义如下：

\mathcal{S}_R^{(k)} = \{i \in \mathcal{S} \mid r_i \leq k\}, \tag{10}

其中 k 是一个超参数。随后，我们定义主成分熵为：

\mathcal{H}_P^{(k)}(p) = -\sum_{i \in \mathcal{S}_R^{(k)}} p_i \log p_i. \tag{11}

然后，主成分熵被用作最小化目标，以替代公式 (8) 中定义的熵：

\mathcal{L}_{PEM} = \mathcal{H}_P^{(k)}(p). \tag{12}

最终的损失函数可以表示为：

\mathcal{L} = \lambda \mathcal{L}_{AB} + \mathcal{L}_{PEM} \tag{13}

4 实验

4.1 实验设置

数据集：Kinetics50-C 和 VGGSound-C
损坏：15种视频损坏、6种音频损坏、5个级别
基线：Tent、MMT、EATA、SAR、READ
实验细节
- 模型：CAV-MAE
- 超参数k在两个数据集上分别设置为8和30
- \lambda = 1
- 为了与（Yang 等，2024）保持一致，还使用了类别平衡损失（class-balancing loss）。

4.2 性能对比

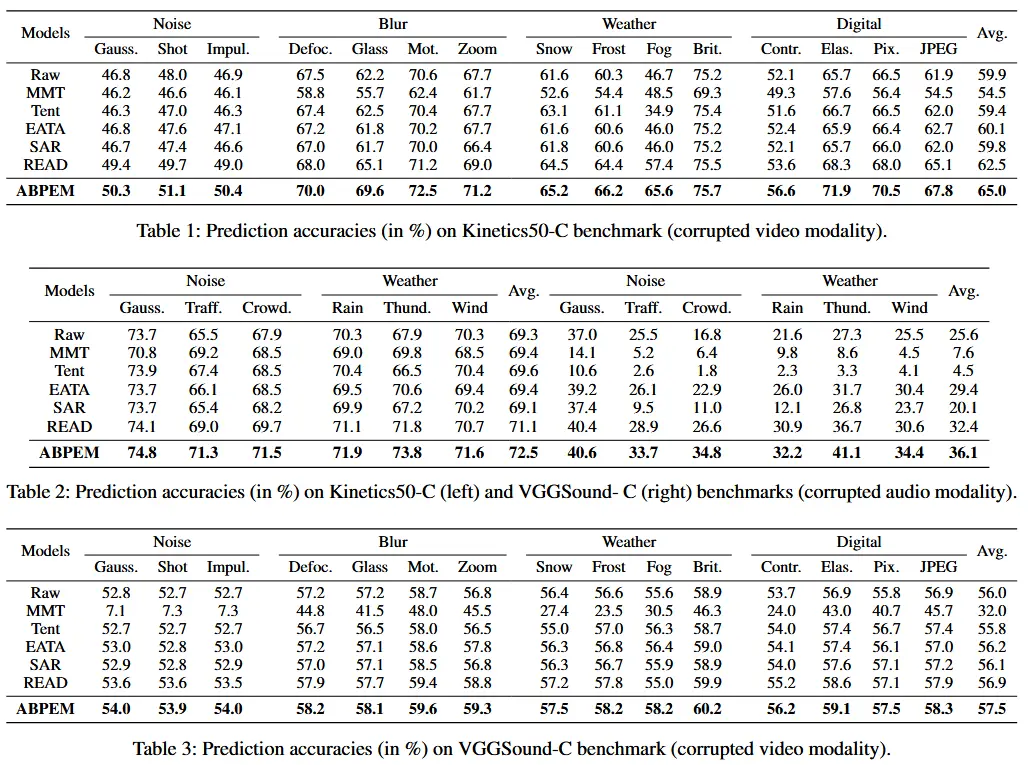
表 1、表 2 和表 3
- ABPEM 在面对各种类型的测试时间分布偏移时，均表现出一致的领先优势。
- 当面对影响信息量更大的模态的测试时间分布偏移时（例如 Kinetics50-C 中受损的视频模态和 VGGSound-C 中受损的音频模态），ABPEM 表现出了更显著的提升。以往的研究往往忽视了注意力差距增加的问题。

4.3 消融实验

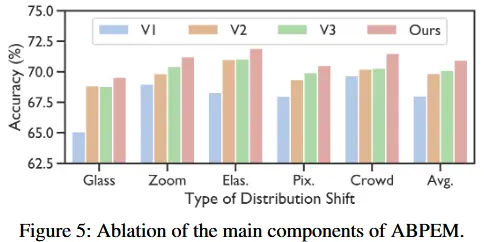
变体
- V1 ：采用可调层，并使用 (Yang et al., 2024) 中的基本自监督目标。
- V2 ：在 V1 的基础上引入注意力引导 。
- V3 ：将主成分熵最小化替换为普通的熵最小化。
- ABPEM ：包含注意力引导和主成分熵最小化的完整模型。
与变体的消融实验

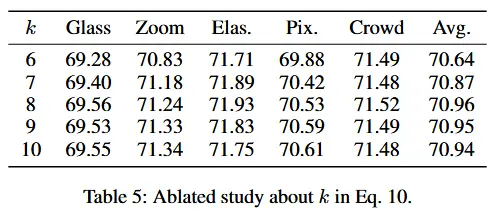
公式10中k的消融实验
- 模型对 k 的选择总体不敏感，在 k=8 时达到最高准确率。

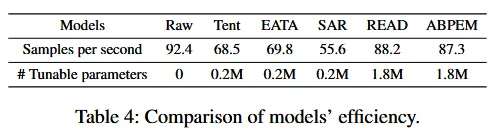
效率对比
- ABPEM 在处理速度（每秒样本数）上与 READ 方法相当。
- 它比需要调整层归一化模块的方法（如 Tent 、EATA 和 SAR ）更快。

论文笔记《Attention Bootstrapping for Multi-Modal Test-Time Adaptation》

摘要