摘要
- 问题背景
- 微型企业和个人开发者对使用强大的大型语言模型(LLMs)进行长上下文分析的需求不断涌现。他们尝试在本地部署这些LLMs,但仅拥有各种商用设备以及设备之间不稳定的互联条件。现有的并行技术在有限的环境下无法完全发挥作用。设备的异构性,加上其有限的容量和高昂的通信成本,为私有化部署带来了挑战——如何最大化利用可用设备的同时隐藏延迟成为难题。
- 提出解决方案
- HPipe,一种流水线推理框架,成功将LLMs从高性能集群迁移到异构的商用设备上。通过确保工作负载的均衡分布,HPipe通过在token维度上对序列进行流水线处理来加速推理过程。
- 评估
- 在LLaMA-7B和GPT3-2B上的评估表明,HPipe具备在异构设备上支持长上下文分析的潜力,在延迟和吞吐量方面实现了令人印象深刻的加速,最高可达2.28倍。
1 介绍
- 现有方法
- 方法:为了满足高效推理的需求,推理引擎(Aminabadi等,2022b;Li等,2023)提供了混合数据并行和流水线并行(Huang等,2019;Narayanan等,2021),并与张量并行(Shoeybi等,2019;Jia等,2019)相结合。
- 优点:在高性能计算中心,这些技术显著减轻了计算和内存压力,从而提高了推理速度并增强了吞吐量。
- 现有的方法无法直接适用于微型企业的场景,面临以下几个问题:
- 扩展文本 :随着LLM支持更长的输入,扩展的上下文窗口带来了更高的计算压力。微批次流水线难以维持效率。流水线的每个阶段都需要更长的处理时间,而较粗的粒度降低了并行性。
- 通信差异 :设备之间的通信条件存在差异。设备内部的GPU通常通过PCIe交换数据,而设备之间的GPU则依赖网络通信。这阻碍了诸如张量并行等通信密集型方法的效果。
- 异构设备 :整合异构设备以充分利用所有可用资源对微型企业至关重要。计算和传输的双重异构性,加上高昂的通信成本,为协调微型企业可用设备以部署LLM带来了挑战。
- 解决
- 作者提出了 HPipe ,一种专为私有化LLM内容理解设计的流水线推理框架。
- 它通过在token维度上应用流水线并行,将LLM部署在异构设备上。HPipe 根据计算能力和传输条件分配LLM,从而屏蔽设备的异构性。
- 对于扩展的上下文,HPipe 使用动态规划算法将其切分为多个片段,并对这些片段的计算进行流水线处理,以提高并行度。
- HPipe 成功将LLM从高性能集群迁移到异构设备上,在延迟和吞吐量方面实现了高达 2.28倍 的提升,同时与其他方法相比,能耗降低了 68.2% 。
2 背景和动机
2.1 并行
- 张量并行
- LLM计算特性:矩阵乘法(MatMul)占据了整体计算量的绝大部分。解决一个MatMul问题可以转化为求解多个较小MatMul的总和。
- 张量并行利用这一特性,通过将权重矩阵分割并分配到多个设备上以实现并行计算。一旦计算完成,设备之间需要通信以同步结果。因此,张量并行通常在传输条件有保障的情况下使用。
- 流水线并行
- 流水线机制将LLM分布在多个设备上,每个设备负责计算的一个阶段。请求通常被分割为微批次(micro-batches)并依次处理。流水线仅需传输中间结果,因此通信开销较轻。
- 然而,在批处理维度上的流水线对服务于微型企业的LLM仍带来挑战。
- 内存限制了请求的批处理大小,这减少了数据划分的空间并阻碍了并行度的提升。
- 此外,随着序列长度的增加,每个流水线阶段需要花费更多时间。阶段执行时间的增加导致更多的空闲等待。
2.2 设备利用率
- 一次性处理超长序列可能会使设备不堪重负,而处理短序列则容易导致计算能力的浪费。
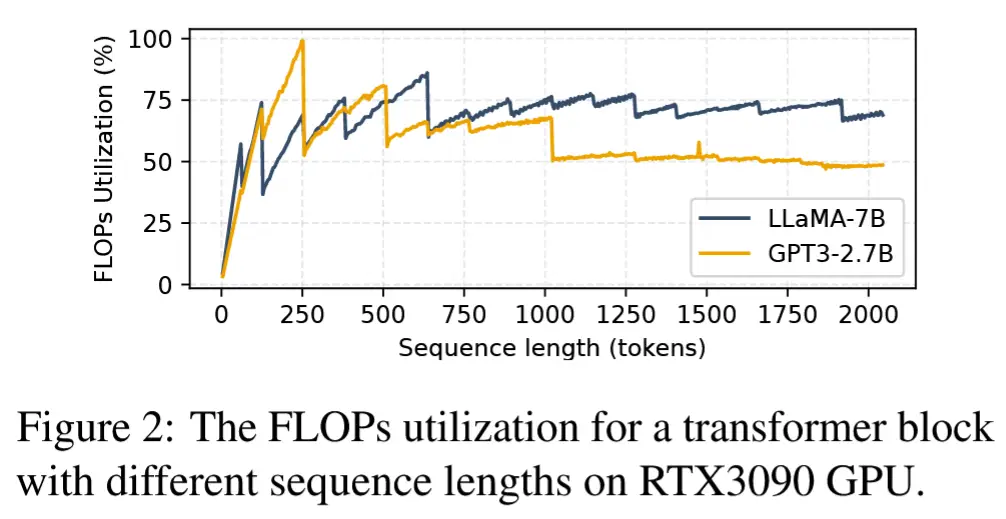
- 为了探索序列长度与资源利用率之间的关系,引入了FLOPs利用率 的概念,即实际达到的每秒浮点运算次数(FLOPs)与硬件支持的最大FLOPs的比值。图2展示了相关结果。
- 结论:随着序列长度的增加,FLOPs利用率最初会提高,随后在收敛前出现下降。
- 分析:起初,随着更多token输入,资源逐渐被充分利用,FLOPs利用率随之上升。然而,最终收益受到频繁I/O操作的限制。低带宽的内存访问成为瓶颈,尤其是在涉及更长嵌入向量时。
- 波动现象:在序列长度增加时观察到波动现象。
- 原因:GPU通过将矩阵划分为小块(tiles)并行处理不同的线程块(thread blocks)来执行矩阵乘法(MatMul),其中线程块是指一组执行相同算术运算的线程。因此,当矩阵维度能够被小块大小整除时,MatMul能够实现GPU的最大利用率。否则,由于小块量化,某些线程块会进行无效计算。
- 结论:因此,为每个处理阶段选择适当的序列长度可以提高设备利用率。
2.3 动机
- 动机
- 流水线并行它能够减少大量的计算负载,同时仅引入可接受的通信开销,适合资源受限的场景。
- 此外,基于解码器的Transformer架构天然适合流水线推理。它允许在token维度上对长上下文进行流水线处理,这不会影响结果,因为子序列是按顺序输入的。
3 方法
3.1 Workflow
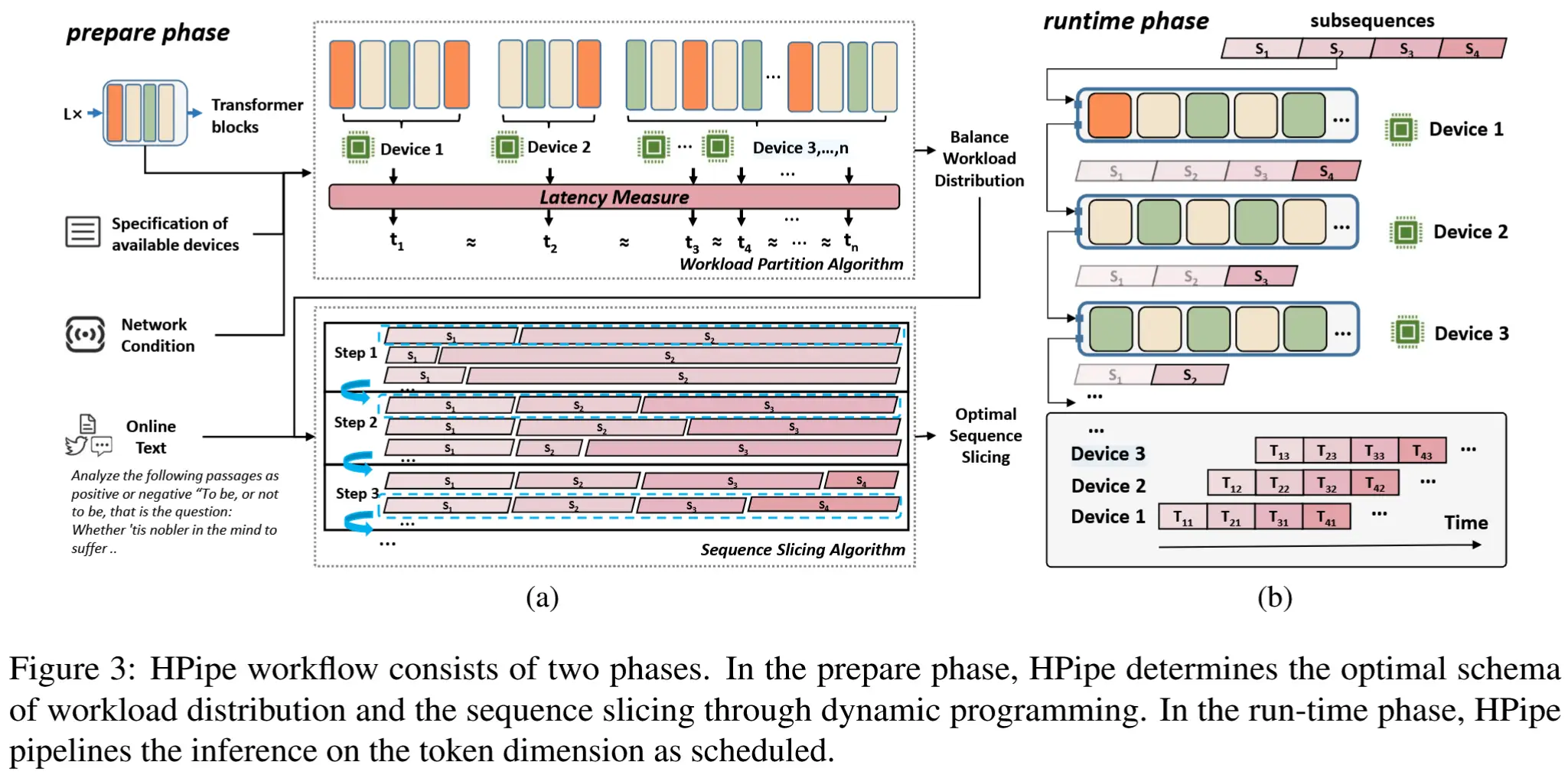
- HPipe工作流
- 下图展示了HPipe的工作流程。
- LLM模型切片:考虑到设备规格和网络条件,LLM被合理地分布到多个设备上,以最大化每个设备的利用率,同时避免过高的传输开销。
- 输入序列切片:HPipe预先处理了所有支持长度输入的最优切片方案。一旦一个序列 S 到达,它会被分割为子序列 s_0, ..., s_m ,并在设备上依次执行。
- 设备 d_i 可以处理子序列 s_i 的计算任务,其中涉及 s_{i+1} 和 s_{i-1} 分别在设备 d_{i-1} 和 d_{i+1} 上的处理。这有效地重建了流水线,实现了在token维度上的并行处理。
3.2 公式化
- 模型符号表示
- 假设LLM由 n 层 \{l_1, ..., l_n\} 组成,这些层被划分为 N 个块 \{b_1, ..., b_n\},并分布到 N 个设备上。
- 同时,输入序列在token维度上被分割为 M 个子序列。
- 用 t_{ij} 表示流水线中每个阶段的执行时间,它是子序列 s_i 在设备 d_j 上的计算时间加上传输到下一个设备 d_{j+1}的时间。
-
子序列嵌入的计算包括两个步骤:计算token的初始嵌入 & 结合前序token的信息与相关性分数。
-
传输时间与最后一层 l_j 生成的中间激活值的大小以及带宽 B 相关。
-
执行时间 t_{ij} 可以表示为:
t_{ij} = t_c (s_i, \sum^{i-1}_{m=1}s_m;d_j) + t_t(l_j,s_i,B)- t_c 表示给定子序列 s_i 及其前序子序列 s_1, ..., s_{i-1} 的整体计算延迟,用 t_t 表示传输时间。
-
- 约束条件
-
目标是找到一种均衡的工作负载划分
\{b_1, ..., b_n\}和适当的切片方案 \{s_0 ,..., s_m\},以实现最优的延迟 \mathcal{T}^*_O ,尽可能接近图3所示的理想状态。 -
为了提高流水线的效率,必须均衡各阶段的执行时间。为此,建立一个约束条件,逐步逼近最优方案:
\mathcal{T}^* \leq \max_{i \in N} \left\{ \sum_{j=0}^{M} t_{ij} \right\} + (N-1) \max_{\substack{0 \leq i < M, \\ 0 \leq j < N}} \{t_{ij}\}.- 第一项是最慢设备上的完整推理延迟 ;第二项是由流水线执行带来的开销,其大小由最慢的阶段 决定。该约束条件通过限制延迟的上限,使能够确定最优解。
-
由此可知,缩小设备之间和阶段之间的差距 将有助于提升流水线推理效率。通过均衡分布 和序列调度 来实现流水线推理的均等化。
-
3.3 分布式平衡
- 一种均衡的模型划分 可以最大限度地减少设备和传输条件中存在的异构性影响。首先通过将LLM分配到与设备能力相匹配的方式来优化流水线,同时考虑传输开销。
- 本文以 层(layer) 为划分粒度,而不是Transformer块,这为探索更均衡的划分提供了机会。均衡分布的目标是找到 N-1 个切割点,将LLM划分为 N 个子集,每个子集包含连续的层并分配给特定设备。
- 假设设备的顺序保持不变,即块 b_j 对应设备 d_j。由于LLM由重复的块组成,设备顺序的固定几乎不会丢失最优解,从而使问题得以简化。
- 在设备 dₘ 上处理从层 l_{a+1} 到 l_b 的执行时间
-
包括两个部分:这些层的累积计算时间+传输中间激活值的通信时间。
-
可以通过以下公式计算
T(a,b,m) = \sum^b_{k=a}t_{comp}(l_k;d_m)+t_{comm}(l_j,m)
-
- 最优划分
-
可以将其分解为一个由 l_1 到 l_k 层组成的最优子流水线 ,该子流水线分布在 m-1 个设备上,随后是一个单阶段的执行,包含 l_{k+1} 到 l_b 层,并运行在设备 d_m 上。
-
利用最优子问题性质 ,可以确定一种分配方案,逐步均衡各设备之间的执行时间:
\mathbf{A}[b][m] = \min_{1 \leq k < j} \left\{ \max \left\{ \mathbf{A}[k][m-1], T(k+1, b, m) \right\} \right\} -
其中,A[b][m − 1] 表示在前 m-1 个边缘设备上,从 l_1 到 l_b 的最优子流水线中最慢阶段的执行时间。
-

3.4 序列调度
-
通过最优切片策略 进一步优化流水线。一些研究(Zheng等, 2023;Li等, 2021)观察到,token的执行时间随着位置索引的增长而线性增加,因为计算中涉及的前序token数量更多。因此,理想的切片方案应包括开头较长的切片 和结尾较短的切片 。
-
划分序列的粒度也非常重要。采用细粒度切片 (即较小的 |sᵢ| 值)会导致GPU计算能力的利用率不足;而采用粗粒度切片 (即较大的 |sᵢ| 值),虽然减少了流水线阶段的数量,但会降低并行度,并可能使设备负担过重。
-
列举可能的 t_m 以从切片空间 S 中找到最佳切片 S∗:
\mathcal{T}^* \leq \min_{t_m} \left\{ \max_{i \in N} \left\{ \min_{S^* \in \mathcal{S}} \left\{ \sum_{j=0}^{M} t_{ij} \mid t_{ij} \leq t_m \right\} \right\} + (N-1)t_m \right\}.- t_m 将每个切片的执行时间限制为相似,从而将流水线延迟降至最低。
- 由于序列 S 的优化可以从 S − s_n 派生,因此采用动态规划算法在所有可能的 t_m 中产生最佳切片模式。

4 实验
4.1 实验设置
- 硬件配置:使用由两台主机组成的计算集群,第一台主机配备4块Pascal100 (P100) GPU,第二台主机配备2块RTX3090 GPU。
- 通信:
- 主机间通信:通过带宽为1000 Mbps的有线网络。
- 主机内通信:通过PCIe。
- 模型:GPT3-2B、LLaMA-7B
4.2 性能
- 对比方法
- Base:LLM均匀分布在每个GPU上,集群中按顺序执行推理。
- GPipe:将LLM均匀分布在GPU上,并通过微批次(micro-batch)实现流水线推理。
- GP-B:在GPipe基础上,采用HPipe提出的工作负载分配策略
- Megatron-LM:结合张量并行 和GPipe的流水线技术。
- TeraPipe: 将LLM均匀分布在GPU上,并在token维度 上实现流水线推理。
- TP-T:在TeraPipe基础上结合张量并行
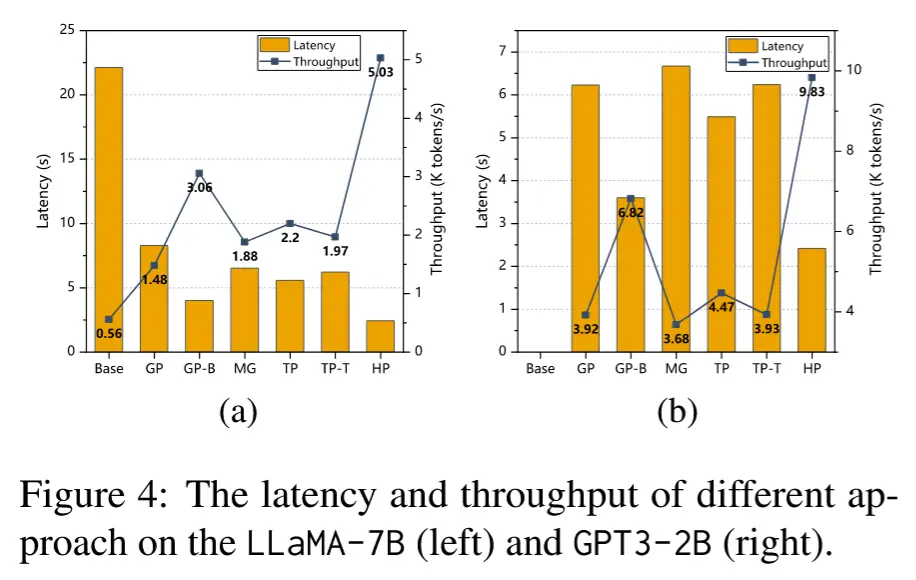
4.2.1 延迟和吞吐量
- HPipe在延迟和吞吐量上的表现显著优于其他方法,特别是在长序列推理任务中。
- 其成功的关键在于细粒度流水线推理 、负载均衡分配 以及对通信开销的有效控制 。
- 张量并行与token维度流水线的结合并不适合,因其引入了过多同步开销。
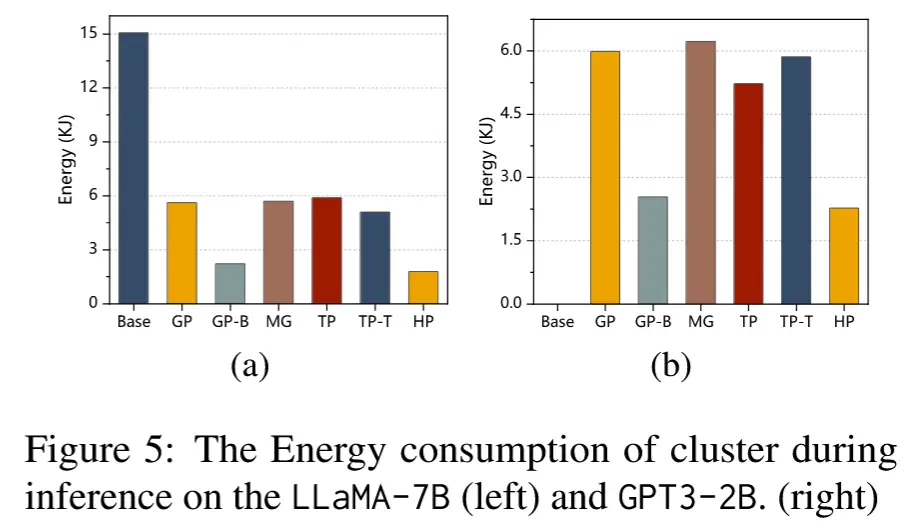
4.2.2 能耗
- HPipe在能耗上的表现优于其他方法,得益于其对异构设备特性的充分考虑和高效的资源利用策略。
- 高资源利用率下的推理执行进一步减少了不必要的能量消耗。
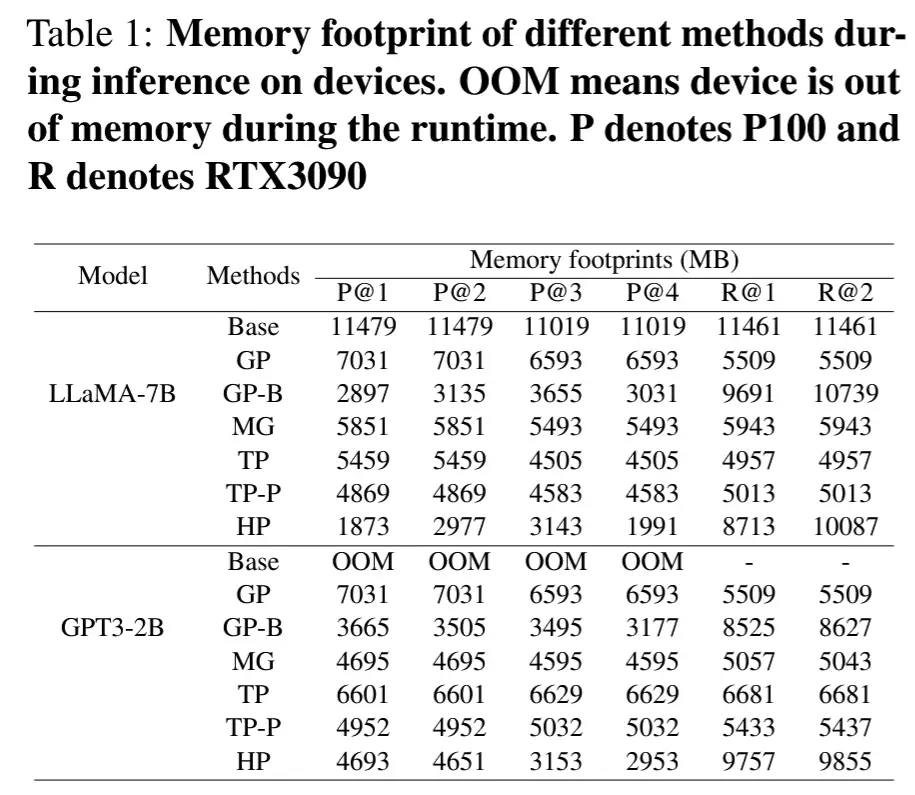
4.2.3 内存占用
- HPipe通过均衡工作负载分配和考虑通信开销,优化了内存使用。
- 在异构环境中,内存占用的差异反映了设备间计算与通信负载的动态调整。
5 结论
本文介绍了 HPipe,这是一个推理框架,用于使用在商用设备集群上原型构建的 LLM 加速内容分析。它有效地集成了计算资源,允许在异构设备上实现精细管道。HPipe 展示了通过长序列输入加速 LLM 推理的潜力,为在异构商用硬件环境中部署 LLM 提供了解决方案。