一、剪枝介绍

什么是剪枝？

剪枝本质：通过去除突触和神经元，使神经网络由稠密变稀疏，冗余度降低。

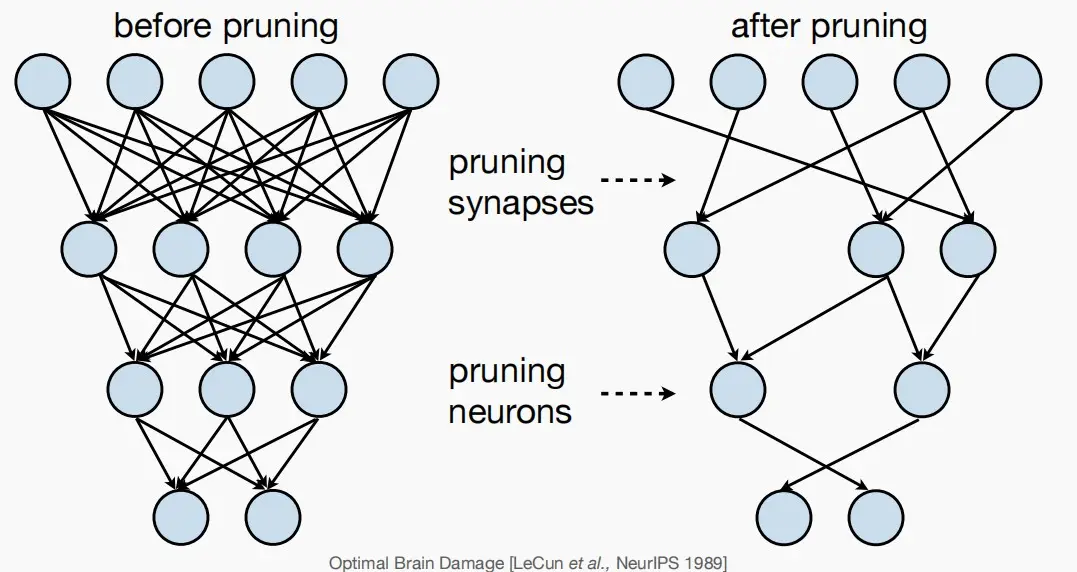
对于图中的曲线

黑色虚线：原模型的基准率
紫色曲线：剪枝，剪去权重较小的权值。剪枝80%后准确率下降4.5%。
绿色曲线：剪枝+微调，最初甚至因减少过拟合而略微提高准确性。
红色曲线：迭代+剪枝+重新训练，准确率可以保持到剪枝90%。

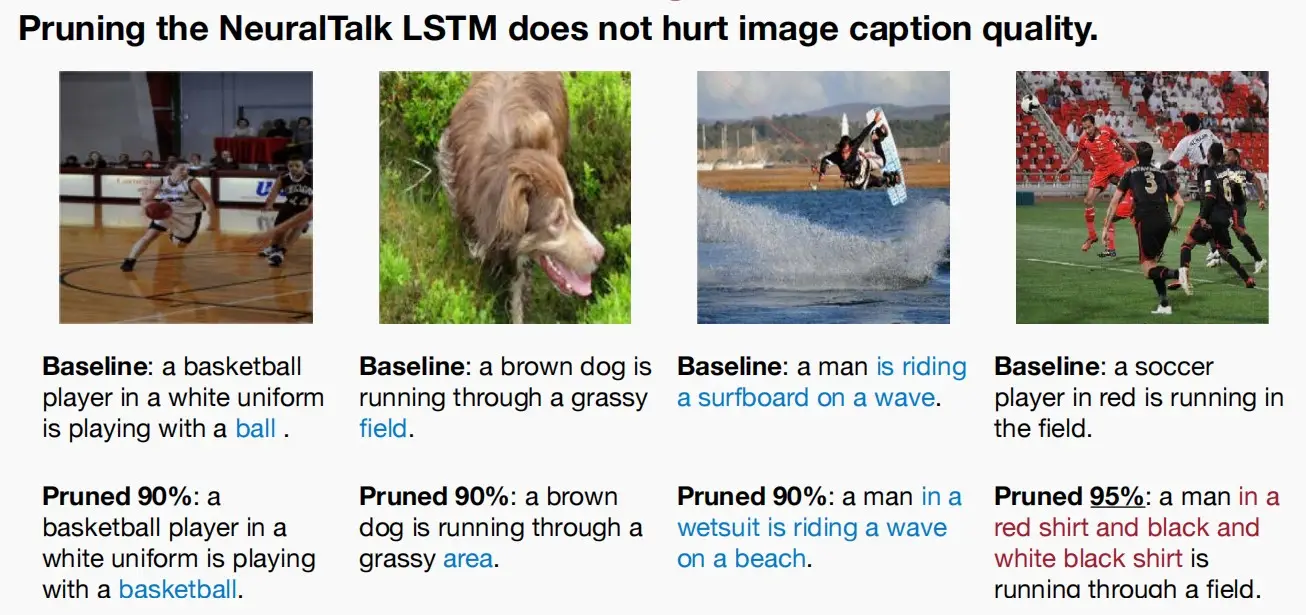
对于图像标题生成模型，当剪枝90%时结果几乎不受影响，而当95%时模型结果质量显著下降，因此剪枝需要一个阈值。

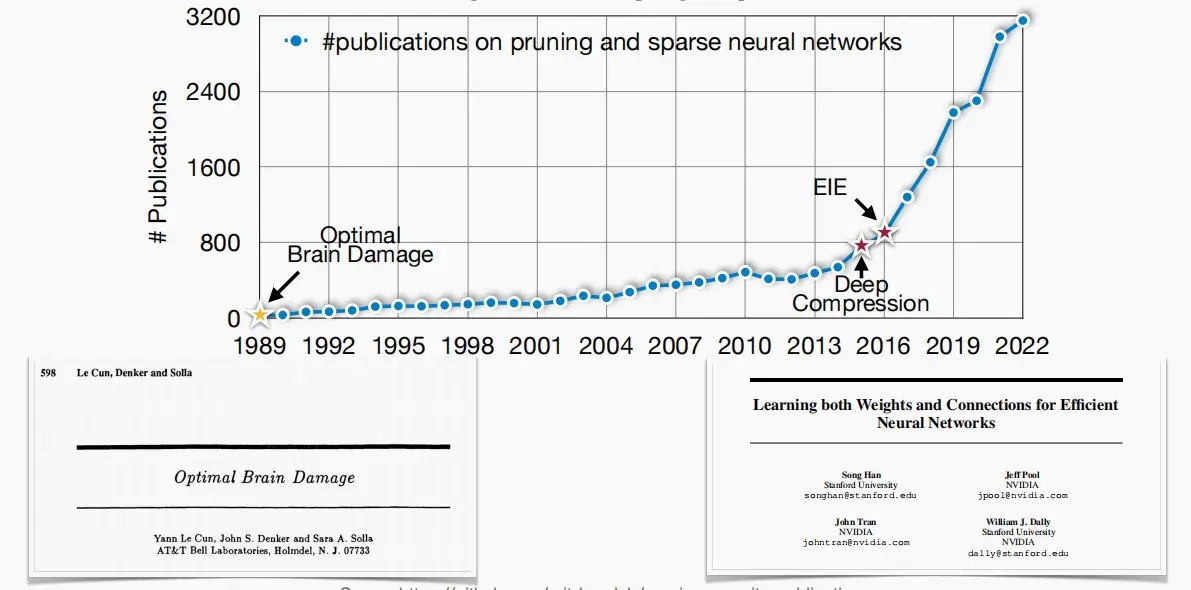
对于剪枝的研究最早可以源自1989年的一篇论文《Optimal Brain Damage》，并且不断发展至今。如今剪枝在工业界也十分流行，比如Nvidia的A100利用了权重稀疏性来加速计算。

如何公式化表述剪枝？

通常我们将剪枝表示为

\argmin_{W_p} L(x; W_p) \quad s.t. \quad ||W_p||_0 < N

其中，
- L 是神经网络训练的目标函数。
- {x} 是输入，{W} 是原始权重，W_p 是剪枝后的权重。
- ||W_p||_0 表示非零元素的个数，N 目标非零权重数。

二、确定修剪粒度

二维权值矩阵

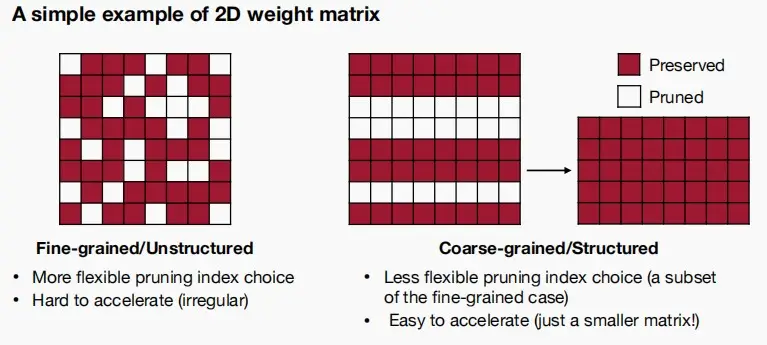
细粒度的非结构化剪枝
- 优点：更大的灵活性
- 缺点：加速难度大，因为其高度不规则，对硬件并行计算不友好。
粗粒度的结构化剪枝
- 优点：经过剪枝后，权重矩阵依旧保持稠密。易于加速。
- 缺点：控制灵活性降低。

卷积层

卷积层的权重有四个维度可以进行剪枝，因此提供了更多剪枝粒度的选择：

输入通道c_{in}
输出通道c_{out}
卷积核的高度k_h
卷积核的宽度k_w

卷积层中的剪枝的例子

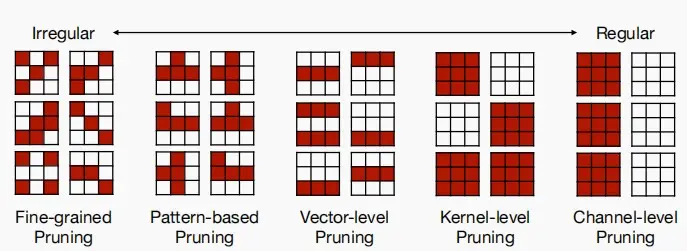
细粒度剪枝：卷积层权重中任意维度任意元素都可以被置为0。
模式级剪枝：通过分析模型中的权重、梯度或其他特征的模式，来决定剪枝哪些神经元或连接。
矢量级剪枝：对一整行或列修剪。
内核级剪枝：对整个卷积核修剪。
通道级剪枝：对整个通道修剪。

细粒度剪枝

更高的压缩比，能识别并去除单个冗余权重。
参数数量的减少≠加速。加速还需要看在硬件上是否易于实现并行和加速。

模式级剪枝

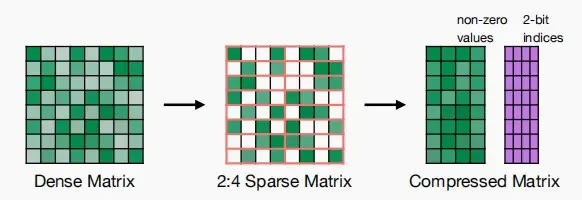
N：M稀疏性：表示在每个相邻的M个元素中，其中的N个被修剪。
它是由NVIDIA的Ampere GPU架构支持的，它提供了约快2倍的速度
通常能较好的保持准确性

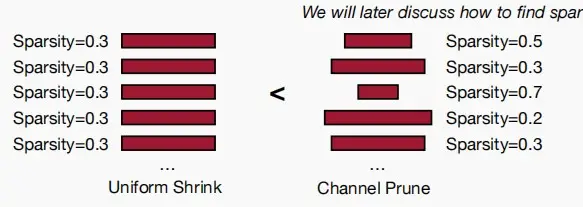
通道级剪枝

优点：剪枝后得到非常稠密的权重矩阵；整个维度上减少一个数字，最容易实现加速。
缺点：压缩比较小。
可以选择各层相同的稀疏度比例，或不同层的不同稀疏度比例。

三、确定剪枝准则

修剪突触

移除的权重越不重要，剪枝后的神经网络性能越好。

基于幅度的修剪

基于大小的剪枝认为绝对值较大的权重比其他权重更重要。

对于元素级的剪枝，每个元素的重要性可以用权重的绝对值表示

Importance = |W|

对于行级别的剪枝，每行的重要性可以用L1-norm或L2-norm表示

Importance = \sum_{i \in S}{|w_i|} \\ Importance = \sqrt{\sum_{i \in S}{|w_i|^2}}

更通常的情况下，幅值用L_p-norm表示

||W^{(S)}||_p = ( \sum_{i \in S} {|w_i|^p})^{1/p}

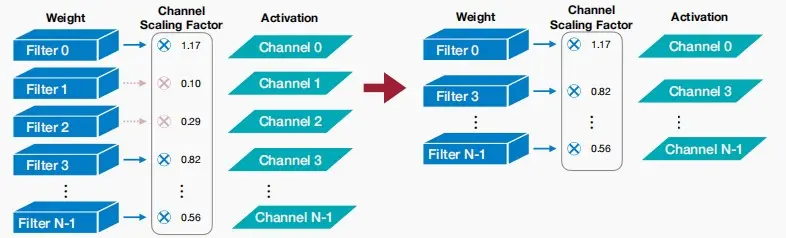
基于缩放的修剪

这个剪枝方法用于卷积过滤核剪枝。在卷积层里每个卷积过滤核都有一个scaling factor缩放因子（可训练的），把这个因子和输出通道的输出乘起来。缩放因子较小的通道将被修剪掉。
这个缩放因子可以用在 BatchNorm 层里。

基于二阶修剪

通过数学推导，可以用泰勒序列来近似剪枝后的损失\delta L
《Optimal Brain Damage》中认为
- 目标函数L是二阶的，最后一项忽视
- 神经网络训练后收敛，一阶项忽视
- 删除每个参数所引起的错误是独立的，交叉项忽视
- 最终只剩下二阶项 \delta L_i \approx 1/2h_{ii}{w_i}^2

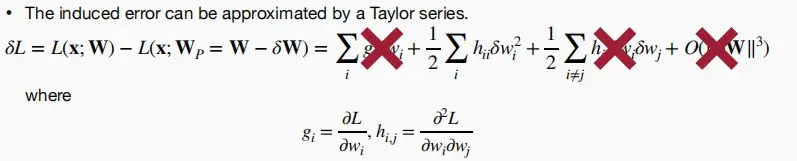
因此我们只需要计算Hessian矩阵，但是由于需要用到二阶导数寻找精确的数字解相当复杂，因此人们开发出了许多近似方法，以避免计算Hessian矩阵。

修剪神经元

同理，还可以对神经元进行剪枝，一旦这个神经元被剪枝，与之关联的所有权重也会被一并剪枝。因此，神经元剪枝本质上是一种粗粒度的权重剪枝。

基于零的修剪百分比

ReLU激活将在输出激活中产生零，希望减少那些主要是0的神经元/通道。
与权重的幅度相似，可以使用 Average Percentage of Zero activations（APoZ，零激活的平均百分比）可以用来测量神经元的重要性。

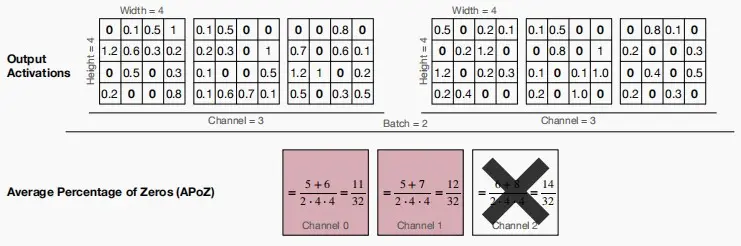
举例：图中有两个 4×4 大小的图片，分别有RGB三个通道，计算三个通道的APoZ，可以看到通道2的APoZ最大，因此剪枝通道2。

基于回归的修剪

基于回归的剪枝使相应层输出的重构误差最小化。
尤其是对于LLMs十分有效。由于LLMs规模巨大，对整个网络进行微调、重建权重非常困难。而基于回归的误差仅关注一层，试图最小化前后变化。

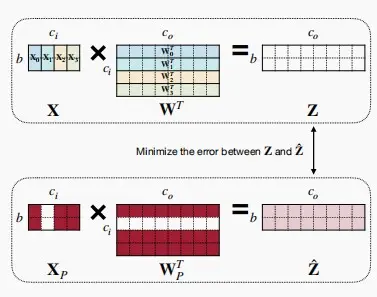
公式表示

令

Z = XW^T =\sum_{c=0}^{c_i-1}{X_c{W_c}^T}

问题可以被公式化为

\argmin_{W,\beta}||Z-\hat{Z}||_F^2 = ||Z - \sum_{c=0}^{c_i-1}\beta_cX_cW_c^T||_F^2 \quad s.t. \quad||\beta||_0 \leq N_c

其中，\beta 是长为 c_i 用于通道选择的系数向量，其中 \beta_c = 0 表示通道c被剪枝。N_c是非零通道的数量，即保留的通道数。

解决问题的步骤

固定 W，迭代学习 \beta。

固定 \beta ，学习 W以最小化重建损失。（使得权重更加贴合剪枝后的模型）

四、确定剪枝比例

本节将介绍三种确定剪枝比例的方法：

敏感性分析
AutoML
NetAdapt

敏感性分析

由于不同的层有不同的敏感度，每一层需要有不同的剪枝率。
- 有些层较敏感，轻微的剪枝便会导致精度急剧下降。
- 有些层较不敏感，即使大幅的剪枝也能保持很好的精度，例如全连接层。

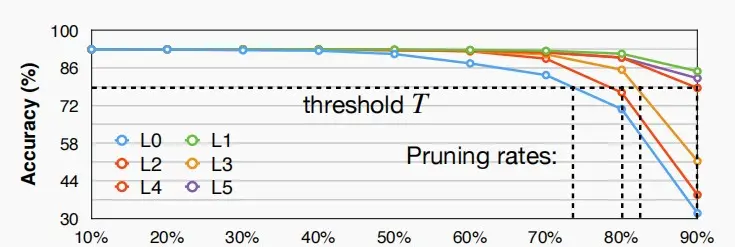
图中为对VGG-11在数据集CIFAR-10上进行的敏感性分析
- 依次选择模型中的一个层 L_i重复下列操作：
  - 对该层进行剪枝，剪枝率分别为 r \in \{0,0.1,0.2,...,0.9\}
  - 观察每个剪枝率的精度降幅 \Delta Acc_r^i
- 选择一个退化阈值 T，以便期望获得总体剪枝率。
但是，本实验仍存在一定的不足之处：
- 没有考虑层与层之间的交互，即裁剪后的互相影响。
- 这种过程依赖于人类的专业知识、反复试验和错误，扩展性不佳。

AMC: AutoML for Model Compression

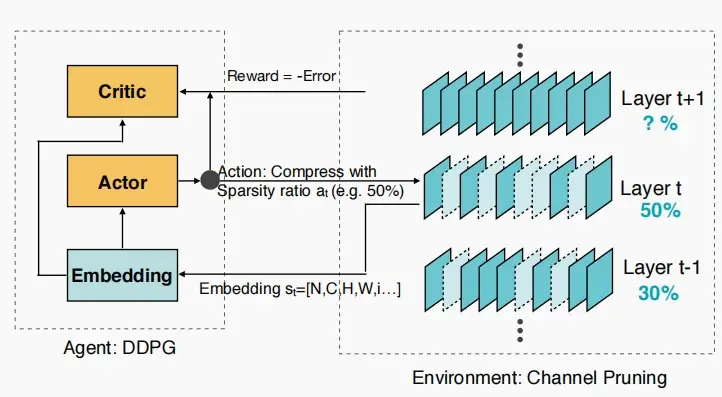
AMC是利用机器学习来解决模型压缩问题设计的解决方案，并采用了Actor-Critic模型。
将模型剪枝问题建模成强化学习问题
- Reward：r = -Error * log(FLOP) ，希望确保FLOPs计算次数尽可能少。
  - 加入 log() 的原因：准确性和操作数OPs形成一种大致的对数关系
- Action：即输出每一层的稀疏比率。
- State：包括图层索引、通道号、内核大小、索引等...
- Agent：DDPG

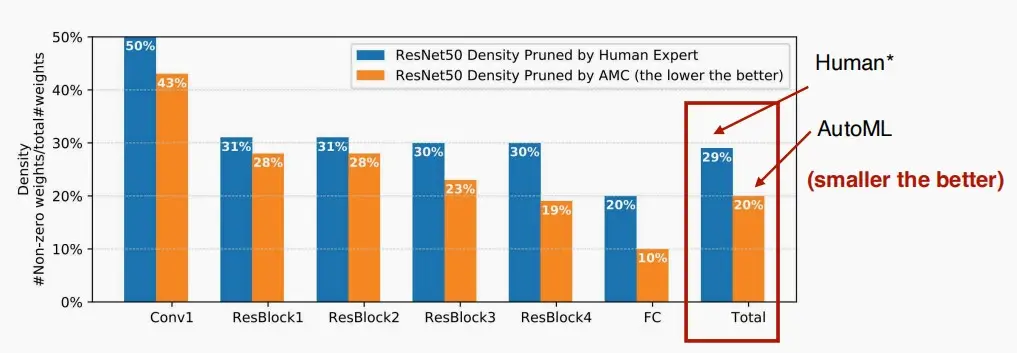
效果图

NetAdapt

NetAdapt: Platform-Aware Neural Network Adaptation for Mobile Applications [Yang et al., ECCV 2018]
一种基于规则的迭代/渐进式的方法
NetAdapt的目标是找到一个每层的修剪比率，以满足一个全局资源约束（例如，延迟，能量，……）
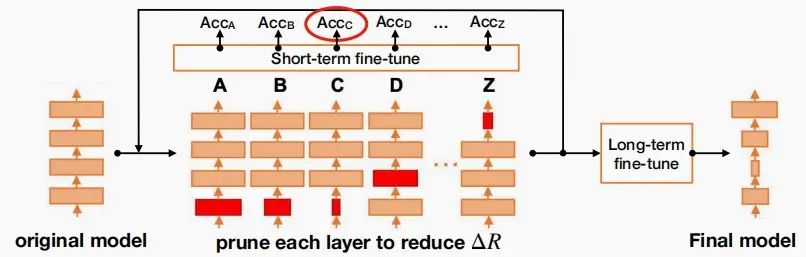
训练流程如下
- 对于每次迭代，手动定义每次迭代希望减少的延迟
- 对各层L_k执行下列操作
- 剪枝，以满足延迟减少 \Delta R
- 短期微调模型，使得准确度恢复
- 选择修剪后精度最高的图层进行剪枝
- 重复此操作，直到总延迟减少满足约束条件
- 长期的微调，以恢复准确性

五、微调/训练已修剪的神经网络

迭代剪枝

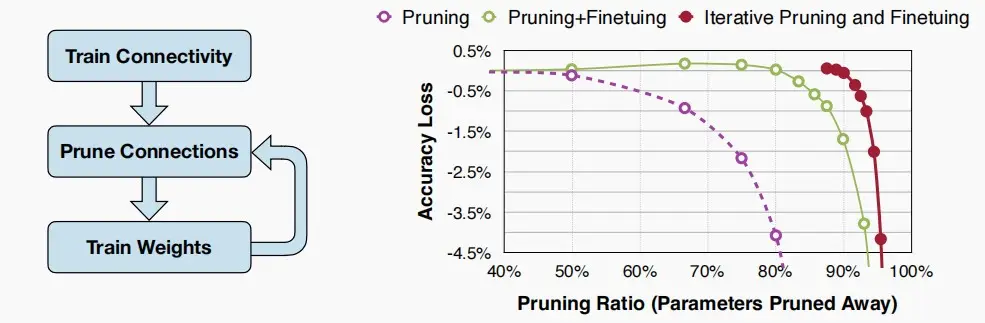
对剪枝后的神经网络进行微调将有助于恢复精度，提高剪枝率。
因此采用迭代剪枝+微调，可以获得更大的剪枝率。

正则化

当训练神经网络或微调量化神经网络时，正则化添加到损失项
- 惩罚非零参数，希望更多的参数为0
- 鼓励更小的参数，有助于下一轮迭代被优化
最常见的正则化方法是L1/L2正则化

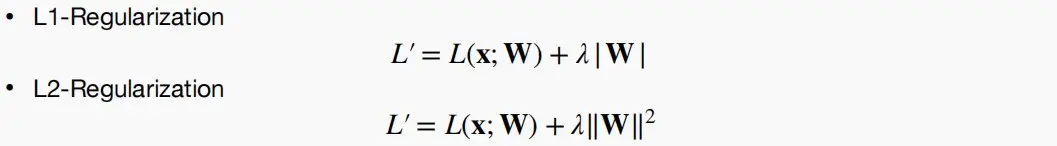
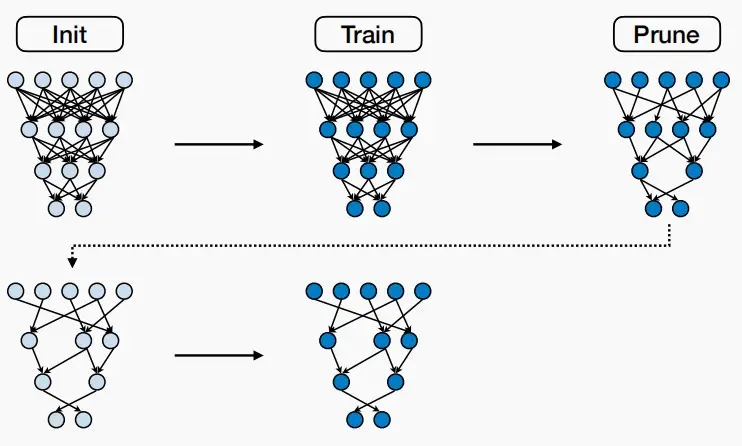
六、《The Lottery Ticket Hypothesis》

该论文探索了在CIFAR和MNIST这类相对简单的任务中，可以从一个稀疏神经网络开始训练至收敛。
一个随机初始化的密集神经网络中包含一个子网络，该子网络在单独训练时，能够在最多相同数量的迭代之后达到与原始网络相同的测试准确性。

七、系统支持的稀疏性

EIE：权重稀疏+激活稀疏的GEMM

稀疏权重：对于权重较小的或者不重要的权重进行剪枝。
稀疏激活：对于激活后为零的神经元进行剪枝。
权重共享：多个神经元或层之间共享相同的权重值，以减少参数的数量和计算负担。

问题：为什么权重减少90%，内存只减少了80%？

答案：因为对于稀疏矩阵，需要索引指示非零权重所在位置。

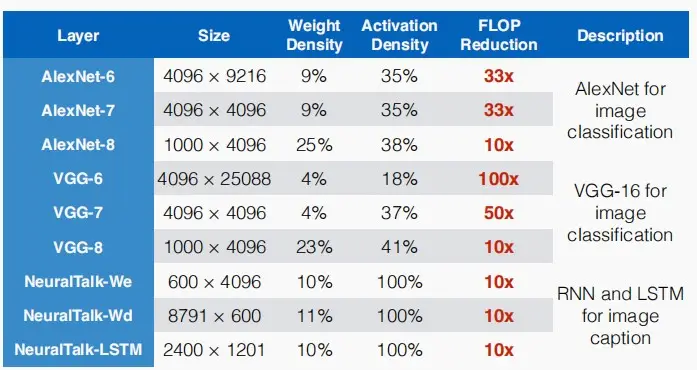
该图展示了FLOP的减少数量。
对于LLMs而言，剪枝技术的效率提升仍然远小于10×，因为微调过程相当具有挑战性。

NVIDIA Tensor Core：M：N权重稀疏

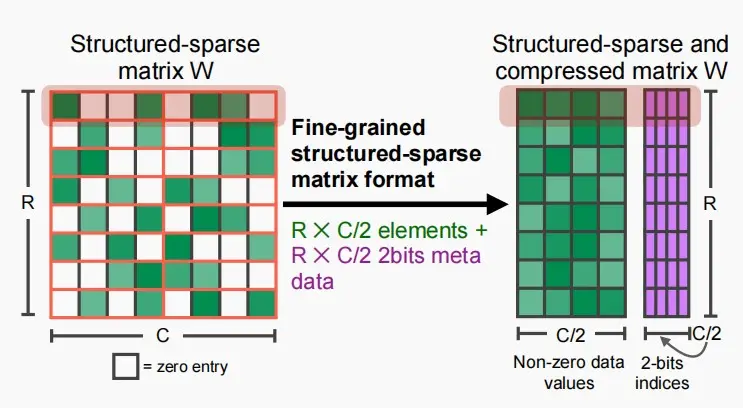
结构化稀疏，使得权重矩阵每四个元素最多有两个非零权重，因此一整行只有四个非零权重。
使用两位的索引存储非零权重的相对位置。

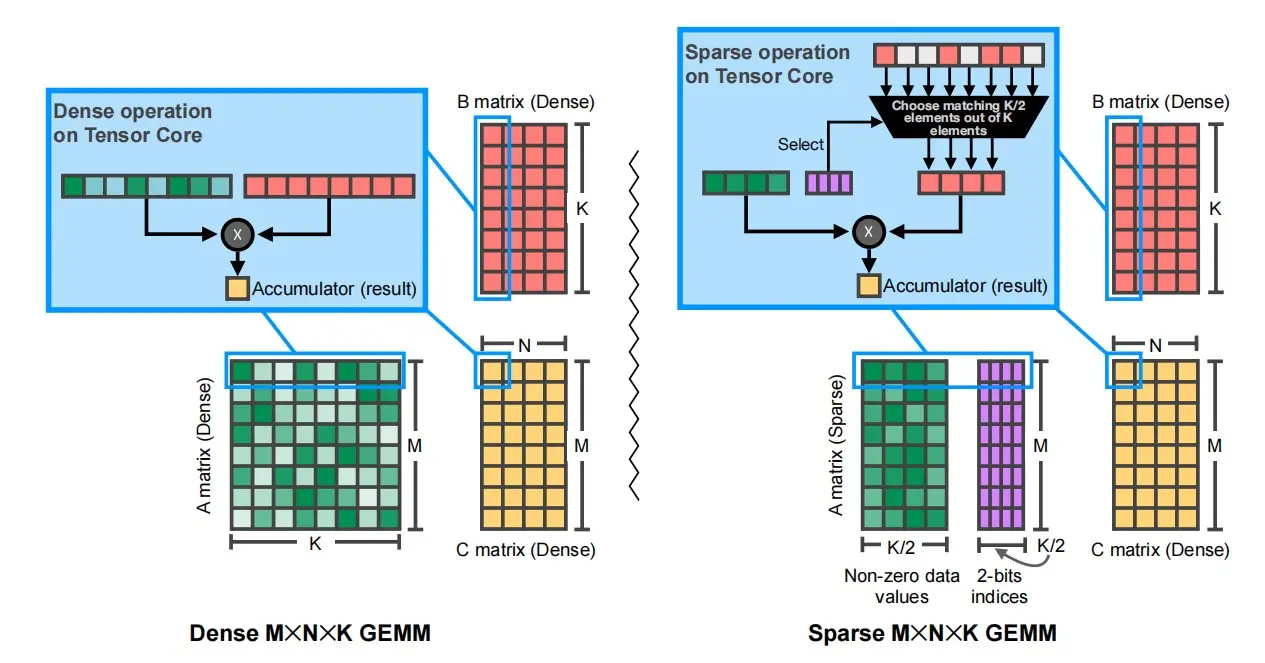
左边是密集权重矩阵，右边是稀疏权重矩阵。
红色的是激活矩阵，黄色的是结果。
可以看到稀疏矩阵激活时，使用索引和多路复用器选择激活值，使得大小相同，避免零权重的乘法。

TorchSparse & PointAcc：稀疏卷积的激活稀疏性

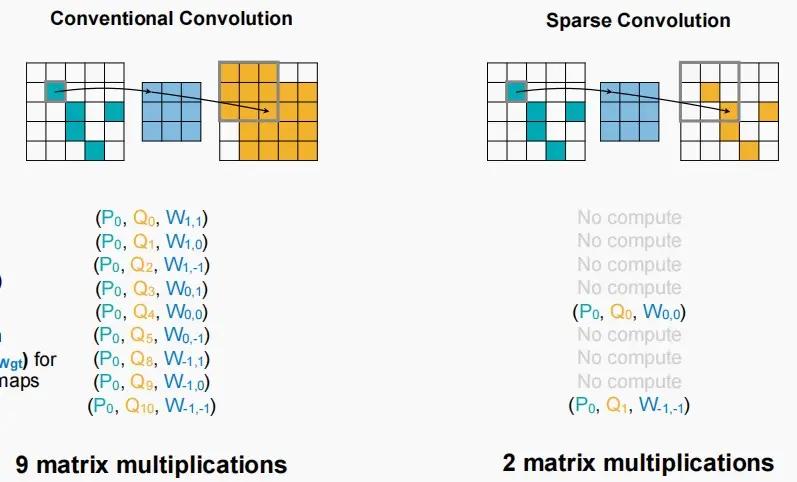
传统的卷积：卷积次数越多，得到的特征图越密集。
稀疏卷积：使得在每一层后能够保持稀疏模式，即非零值依然保持非零，而对于零值依旧保持零。输入与输出具有相同的稀疏模式。

[MIT6.5940] Lect 3&4 - Pruning and Sparsity