一、为什么需要量化？

深度学习中数据的运算大多是浮点数运算，浮点数运算相比整数运算更耗能，而位宽和能耗之间呈现O(n^2)的关系，因此我们希望减少每个权重所占的比特数。

二、数值数据类型

整数Integer
- 无符号整数Unsigned Integer
  - n位表示数值，大小为 [0, 2^n-1]
- 带符号整数Signed Integer
  - 原码表示Sign-Magnitude Representation，n位表示范围为 [-2^{n-1}-1,2^{n-1}-1]
  - 补码表示Two's Complement Representation，n为表示范围 [-2^{n-1}, 2^{n-1}-1]
定点数Fixed-Point Number、
- 固定小数点位置，第0位为符号位，小数点前数值位表示整数，小数点后数值位表示小数。
浮点数Floating-Point Number
- 最常见的为IEEE 754 FP32
- 32bit中，第0位是符号位S，第1~8位是指数位E，第9~31位是小数位M。
- 指数偏移为 2^8-1=127 ，默认数值隐含1。
- 实际值 Value = (-1)^{S} * (1+M) * 2^{E-127}

为了使用更少的比特数来训练神经网络，减少内存占用，使得训练过程更快且成本更低，但也降低了神经网络的精度要求，人们提出了下列几种浮点数格式
- Google Brain Float(BF 16) : 1符号位+8指数位+7小数位
  - 使用BF 16训练的LLMs通常比FP 32更容易收敛，并能避免训练过程中的大动态范围或奇怪的峰值。
  - 模型在训练过程追求更高的动态范围，在推理过程追求更高的精度。
  - 浮点数中指数代表(动态)范围，小数代表精度。因此BF 16其实是用精度换动态范围。
- Nvidia FP8(E4M3)：1符号位+4指数位+3小数位
  - Nvidia在H100中使用了FP8（E4M3）和FP8（E5M2）来进一步减少显存占用，降低通讯带宽要求，提高 GPU 内存读写的吞吐效率。
  - 没有 inf，S.1111.111_2 表示 NaN
  - 最大的规格化值为 𝑆.1111.110_2=448
  - 相比与E5M2有更高的精度，用于前向传播（推理）。
- Nvidia FP8(E5M2)：1符号位+5指数位+2小数位
  - 有 inf（𝑆.11111.00_2）和 NaN（𝑆.11111.𝑋𝑋_2）
  - 最大的规格化值为 𝑆.11110.11_2=57344
  - 相比E4M3有更大的动态范围，用于反向传播时的梯度计算（训练）。

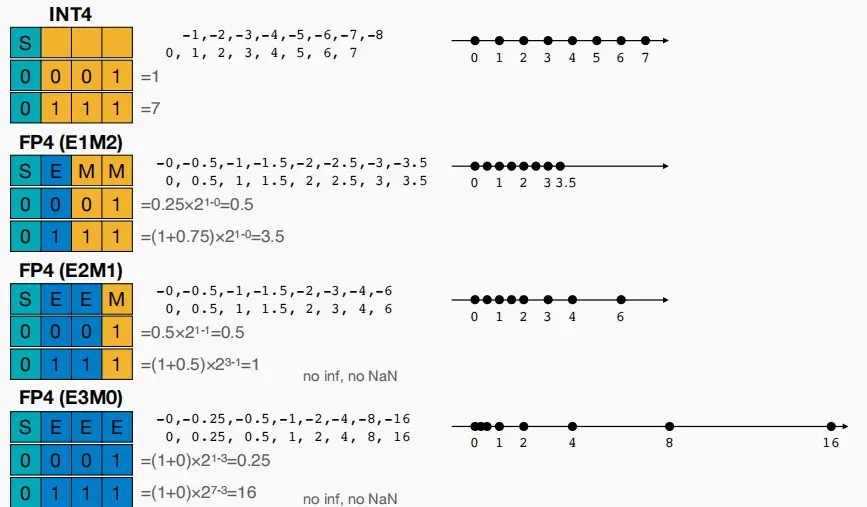
再压缩一下编码位数到4位，此时INT4只能表示-8~7之间的数；FP4有三种编码方式，从E1M2到E3M0动态范围增大而精度减小，如下图所示：

三、什么是量化？

量化是将输入从连续纸或大量值限制到离散集的过程。
真实值与我们表示值的误差为量化误差。

四、常见量化方法

(Ⅰ) K-Means-based Weight Quantization基于K-Means的权重量化

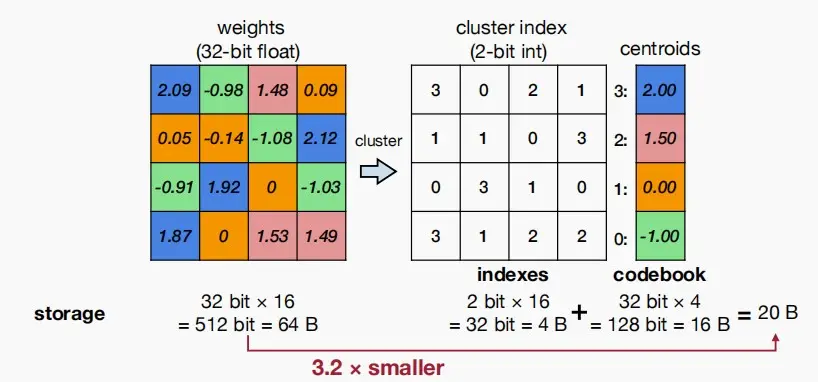
使用K-Means算法对权重进行分类，接近的权重统一着色，然后将同类的数统一替换为与之相近的浮点数。
使用centroids来存储索引和对应的权重数值，并把权重矩阵变成存储索引矩阵。
如下图，可以看出原权重矩阵大小为 32bit * 16 = 64B，使用K-Means量化后大小为 2bit * 16 + 32 bit * 4 = 20 B ，减少了约 3.2 倍。

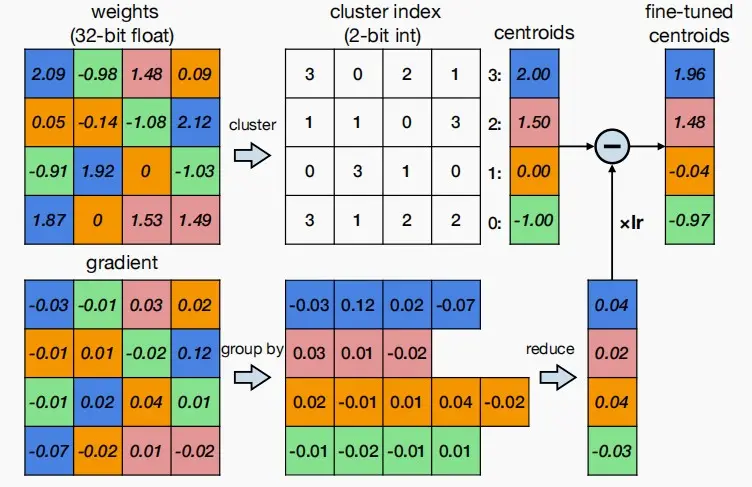
如何进行微调呢？

答：同样对权重梯度进行K-Means量化。

如下图所示，按照权重分类结果对梯度进行分组，对每一组进行求和或求平均，即可得到该组的梯度。
对centroids中的值进行更新，微调后的新centroids等于原centroids减去学习率和梯度的乘积。

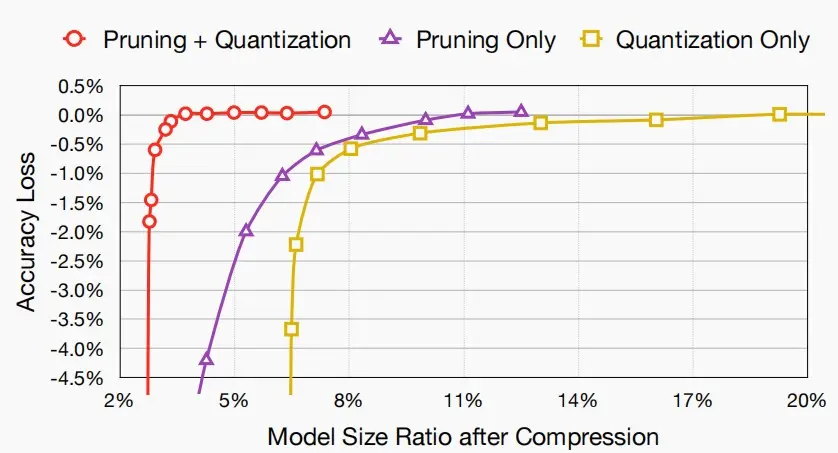
效果图如下，可以看到剪枝和量化的结合能有助于模型进一步压缩，同时保持准确率。

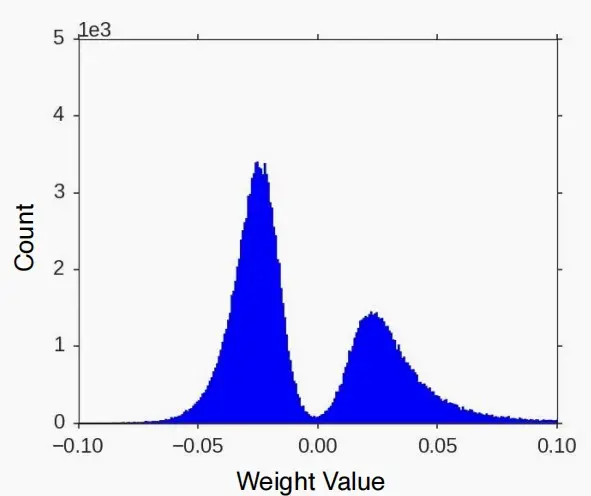
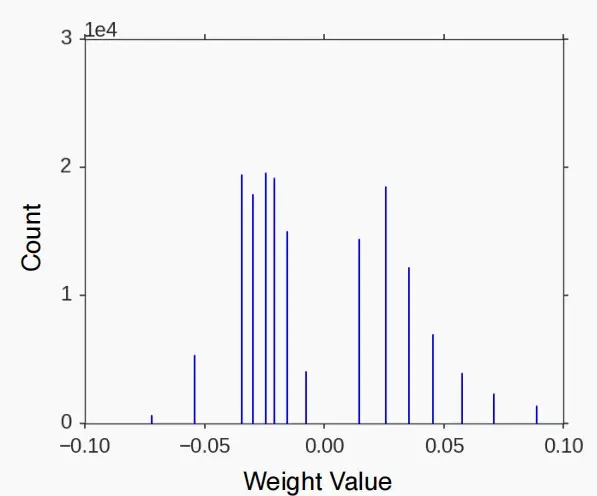
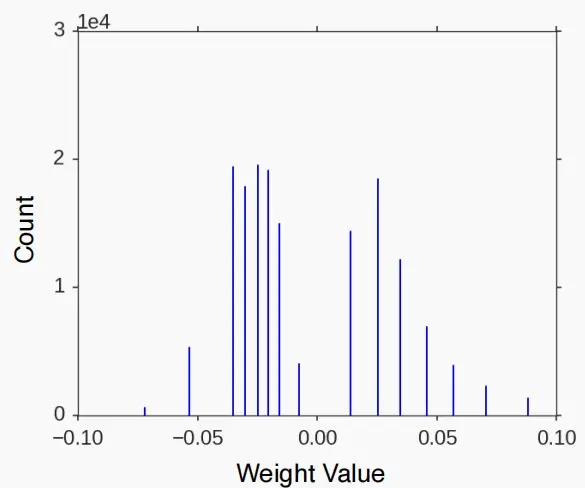
经过量化后，权重图从连续的分布图变成了离散的值。
微调后，离散值产生了轻微的移动。

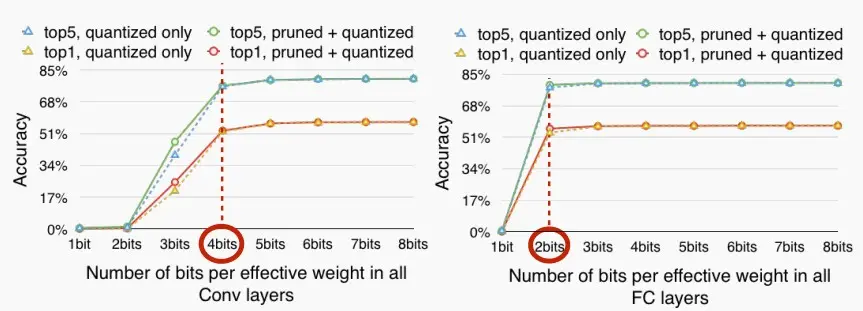
下图展示了编码位数对卷积层和全连接层性能的影响。可以看到卷积层小于4位编码后明显准确率大幅下降，而全连接层小于2位编码后准确率大幅下降。

如何进一步压缩编码位数？

答：使用哈夫曼编码，对于量化后离散的数值位，使用较多位数来表示不常用的权重，较少位数来表示常用的权重。

下图为《Deep Compression》论文的整个压缩流程图，使用了剪枝，聚类量化与Huffman编码。

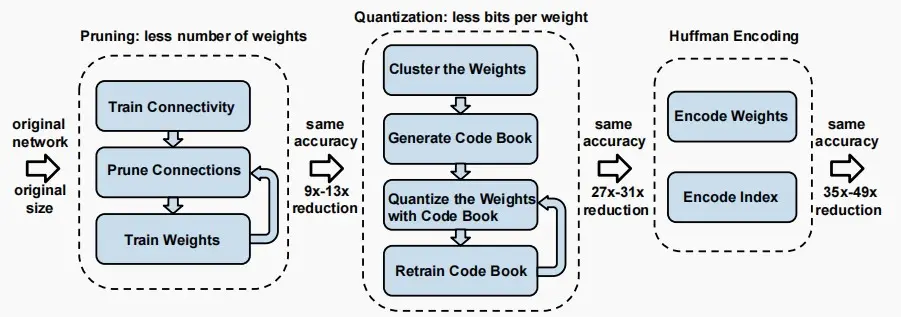
SqueezeNet
- SqueezeNet旨在构建一个小巧实用的神经网络
- 首先通过1×1的卷积，将通道数归于至原始输入的1/4。
- 接着使用两个并行的1×1和3×3卷积，将通道数扩展至原始数量，并进行拼接。
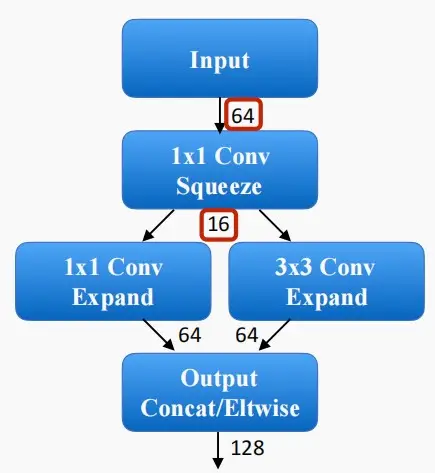
- 可以看到，SqueezeNet比AlexNet的大小相差50倍，使用Deep Compression后相差达到510倍，同时保持了Top1和Top5准确率。

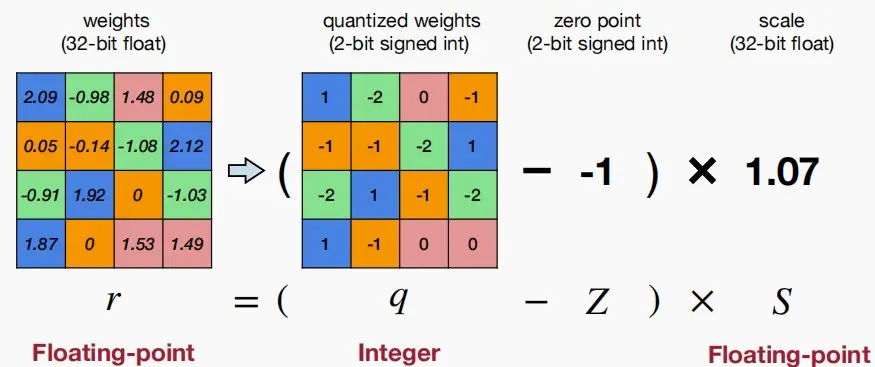
(Ⅱ) Linear Quantization线性量化

如下图所示一种简单的线性量化
图中首先将权重矩阵量化，使用2位有符号数来表示量化后的结果。同时设置2位有符号整数的零点zero point，即映射后的零点；32位浮点数的缩放因子scale。
上述过程可以表示为 r = (q - Z) × S

如何确定两个未知数Z和S？
- 已知 r_{min} 和 r_{max} 与 q_{min} 和q_{max}，以及映射关系。
- 可以得到 S = (r_{max} - r_{min}) / (q_{max} - q_{min}) 与 Z = q_{min} - r_{min}/S

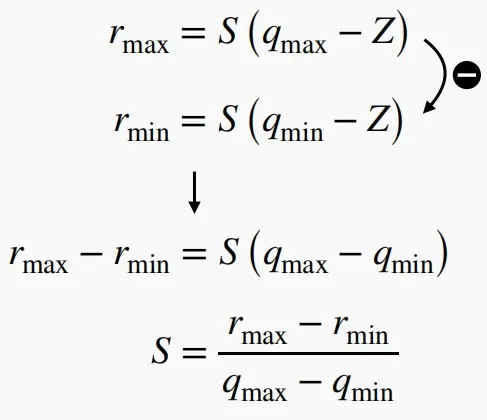
计算Z和S的例子

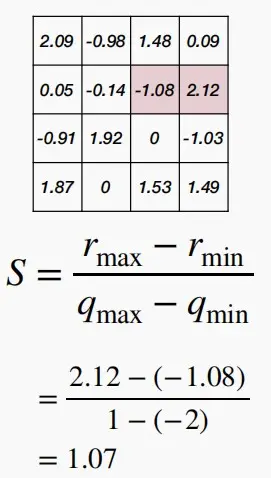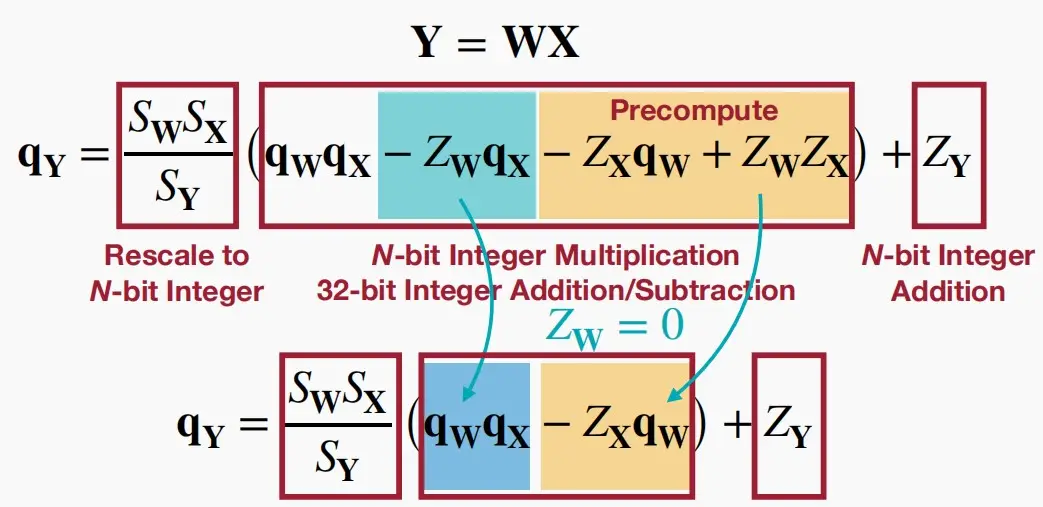
考虑下面的矩阵乘法 Y=WX
根据经验，缩放因子 S_WS_X/S_Y 总是在区间（0、1）内。
Z_W是中心对称分布的，因此可以认为是0，将 Z_W 消去。

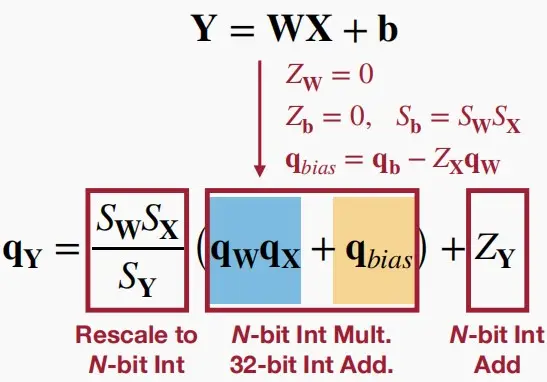
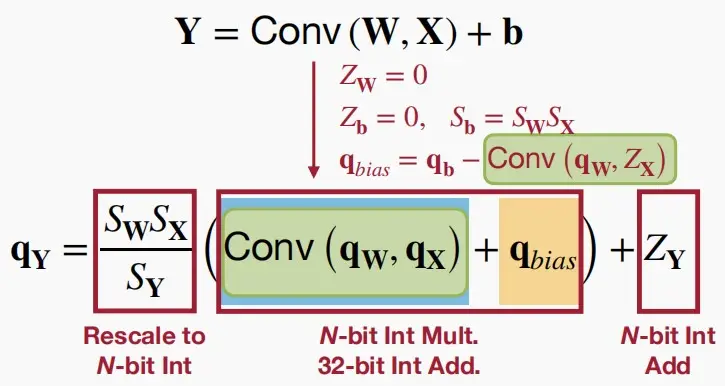
对于带偏置的全连接层进行线性量化 Y=WX+b
- 由于权重对称和偏置对称，为了简化式子同样可设 Z_W = 0 和 𝑍_𝑏=0 ,并令 𝑆_𝑏=𝑆_𝑊𝑆_𝑋
- 再令 q_{bias}= q_b − Z_Xq_W

对于卷积层中线性量化， Y = Conv (W, X) + b ，简化过程类似

(Ⅲ) Post-Training Quantization(PTQ)训练后量化

Quantization Granlularity量化粒度

有以下量化粒度可选
- Pre-Tensor Quantization逐向量量化
- Per-Channel Quantization逐通道量化
- Group Quantization分组量化
  - Pre-Vector Quantization逐向量量化
  - Shared Micro-exponent (MX) data type共享微指数

Pre-Tensor Quantization逐张量量化
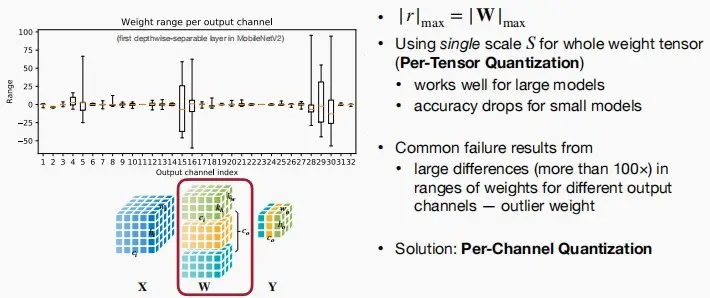
- 张量量化中，取权重的最大绝对值为 |r|_{max}，因此 |r|_{max} = |W|_{max}。
- 对于整个张量使用同一个缩放因子S，对于大模型比较适用，但是对于小模型会精度下降。
- 造成上述失败的原因通常是：不同输出通道的权重范围的大差异（超过100倍）。
- 解决：使用逐通道量化Per-Channel Quantization，即每个通道使用单独的缩放因子。

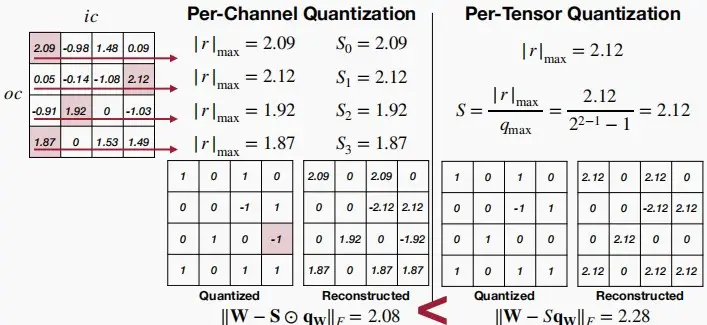
Per-Channel Quantization逐通道量化
- 每个通道使用单独的缩放因子。
- 优点：相比于Per-Tensor Quantization更细粒度，量化误差更小，在视觉模型中表现出色。
- 缺点：需要额外的内存来存储每个通道的缩放因子。
- （注意：下图中两个Quantization矩阵有一处不一样，因为缩放因子不一样。

VS-Quant: Per-vector Scaled Quantization逐向量量化
- 分组量化是更细粒度的量化，对同一个通道里每多少个元素分组做相同的量化处理。
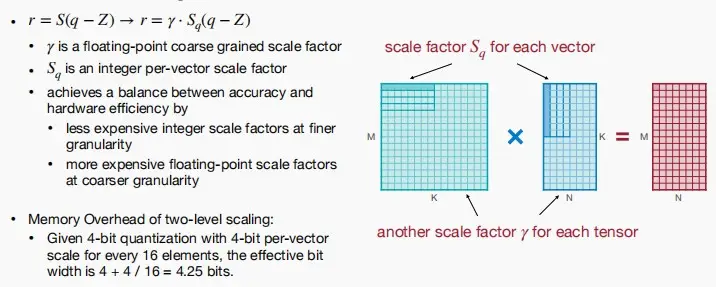
- 原方程 r = S(q-Z) 变为 r = \gamma * S_q(q-z)
  - \gamma 是一个浮点数粗粒度缩放因子，一个张量共享一个 \gamma 。
  - S_q 是一个整数缩放因子，每个向量都有一个单独的 S_q。
- 细粒度采用更便宜的整数缩放因子，而粗粒度使用更昂贵的浮点数缩放因子，以此实现精确率和硬件效率的平衡。
- 例子：如何计算存储凯开销？
  - 给定一个4位量化，即每个缩放因子有4位宽度。每16个元素为一组共享一个4位的缩放因子，则有效位宽度为 4 + 4 / 16 = 4.25 位。

Shared Micro-exponent (MX) data type共享微指数
- 微软使用MX Data Type用于分组量化，分为MX4、MX6和MX9三种，三者尾数位不同拥有不同的精度。
- 如下图五种分组量化：
  - Per-Channel Quant：使用INT4编码量化后的权重；L0 分组按通道分组且缩放因子用FP16编码。
  - VSQ：使用INT4编码量化后的权重；L0 按每16个元素分组，使用UNIT4编码缩放因子；L1按通道分组，使用FP16编码缩放因子。
  - MX：使用S1M2/S1M4/S1M7编码量化后的权重，其中S是符号位，M是尾数位；L0 按每2个元素分组，使用E1M0分组；L1按每16个元素分组，使用E8M0分组。
    - 注意 L0 和 L1 只有指数位，L1 使用16位指数位拥有更高的动态范围。
    - MX后面的数字表示有效位宽，具体计算见下图。

lect6-5webp

Dynamic Range Clipping动态范围裁剪

与权重不同，激活范围因输入而异。
要确定浮点范围，将在部署模型之前收集激活统计信息。
采用激活量化的时刻分为两种：
- 类型一：训练期间
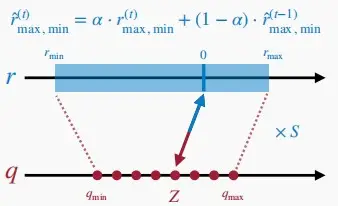
  - 在训练过程中跟踪指数移动平均值。
  - 例如：在每个epoch结束后，检查该特定批次的 R_{min} 和 R_{max}，按照下列公式进行更新。经过数千个epoch后变得范围稳定平滑。
- 类型二：在运行时
  - 使用少量校准数据集来确定R的最大值最小值，这种方式不需要大量的训练.
  - 第一种假设激活值遵循高斯或拉普拉斯函数分布规律。最小化均方误差 \min_{|r|_{max}}E[(X-Q(X)^2)]。例如对于拉普拉斯 (0，b) 分布，最佳削波值可以数值求解为：设为 |r|_{max} = 2.83b,3.89b,5.03b 以适配 2,3,4bits 的量化。
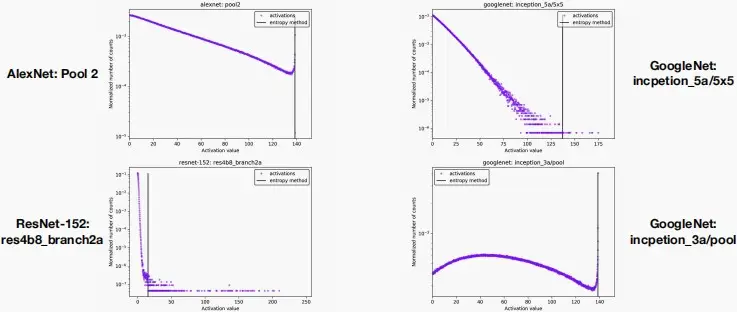
  - 第二种若激活值不遵循函数分布规律。为了最小化信息损失，可以利用KL散度，因为KL散度可以测量在近似给定编码时丢失的信息量，以此来确定最佳的剪枝位置。使用KL散度进行裁剪激活量化的效果如下图：
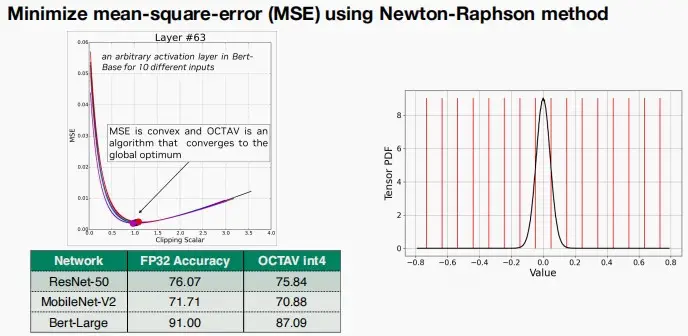
  - 第三种使用Newton-Raphson方法最小化均方误差。定义MSE为目标函数，迭代不同的裁剪力度，寻找最小的均方误差。可以看到图中，随着裁剪标量的增大，MSE先减后增。

Rounding舍入

四舍五入(Rounding-to-nearest)
- 权重是相互关联的。对每个权值四舍五入没有考虑其他张量，因此不是整个张量的最佳舍入
自适应舍入(Adaptive Rounding)
- 不同于四舍五入的\lfloor w \rceil，AdaRound学习从\{\lfloor w \rfloor,\lceil w \rceil\}中进行选择，以得到最好的重建效果。
- 采用一种基于学习的方法来寻找量化的值，\hat{w} = \lfloor \lfloor w \rfloor + \delta \rceil, \delta \in [0,1] 。
- 在自适应舍入中，不在意单个权重，通过权重输出的差异来衡量舍入的影响设计了以下方程：
  - 其中x是该层的输入，V是相同形状的随机变量。
  - h()是一个映射到(0,1)的函数，类似于sigmoid函数。
  - f_{reg}(V) 是正则化项，鼓励 h(V) 二分，即鼓励 h(V) 输出0或1。

\argmin_V||Wx − \lfloor \lfloor W \rfloor + h(V)⌉x ||^2_F + \lambda f_{reg}(V)

(Ⅳ) Quantization-Aware Training (QAT)量化感知训练

通常情况下，如果直接量化一个模型，其精性将会下降。QAT在训练过程中模拟量化的效果（伪量化因子），使得模型能够适应量化带来的信息损失，恢复精度损失。
对预先训练的浮点模型进行微调比从头开始训练提供更好的精度。

“又可称之为在线量化。QAT和PTQ最大的区别是QAT需要数据训练，可以理解为拿着训练好的模型又做了一次微调。而PTQ只是拿少量校准数据调整一些参数。PTQ的优点就是很快，缺点就是还是有一些精度损失，效果不如QAT算法。为了降低量化后准确率的损失，不少方法会在训练时引入量化操作，让量化之后的权重和激活值去参与网络的训练，这种方式称之为量化感知训练即QAT。”

引用自Efficient Deep Learning-学习笔记-4-Model Quantization

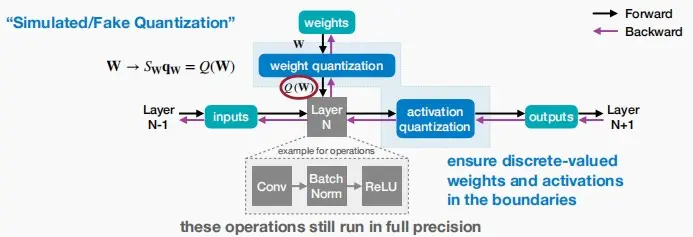
模拟量化：在模型的前向传播过程中，将权重和激活值通过量化和反量化的过程，模拟量化在实际部署中的效果，即权重和激活值先被量化到低位宽的整数表示，然后再被反量化回浮点数。在前向传播时权重会被量化为8位整数，但在反向传播时仍然使用原始的浮点数进行梯度计算，使得模型在训练过程中**“感知”到量化**所带来的误差。
反向传播调整：在反向传播过程中，假量化节点会计算量化误差，并将其纳入到梯度计算中。这样，模型的权重会逐渐调整，以适应量化后的表现。

Straight-Through Estimator (STE)

在神经网络训练中，反向传播算法依赖于链式法则，需要对损失函数相对于每一层参数进行梯度计算。然而，量化函数通常是不可微的（例如取整函数），这就使得直接计算梯度变得困难。因此，STE 被引入来解决这个问题。
STE 的核心思想：在前向传播过程中使用实际的量化函数，而在反向传播过程中，通过一种近似方法来计算梯度，从而使训练过程能够顺利进行。
在反向传播过程中，STE 近似地将量化函数的梯度视为恒等函数的梯度（原本量化函数的梯度应该是恒为0）。这意味着，虽然前向传播使用了量化函数，但在反向传播时，我们假设量化函数对输入的梯度为1。

g_w = \dfrac{\partial{L}}{\partial{W}} = \dfrac{\partial{L}}{\partial{Q(W)}} * \dfrac{\partial{Q(W)}}{\partial{W}} = \dfrac{\partial{L}}{\partial{Q(W)}} * 1 = \dfrac{\partial{L}}{\partial{Q(W)}}

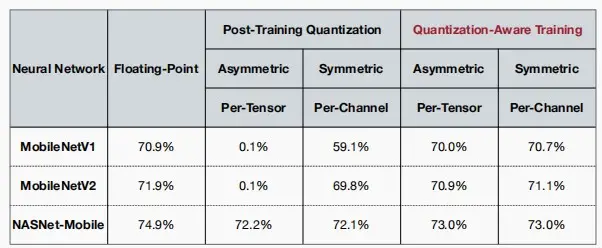
如下图，经过QAT后准确率提升效果显著。尤其是对于Per-Tensor经过QAT后准确率从0.1%提升至70%。

(Ⅴ) Binary/Ternary Quantization二元/三元量化

我们能否将量化精度压缩至一位？
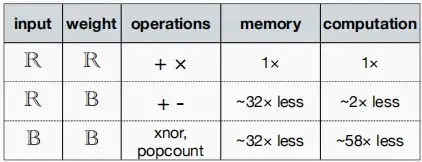
下图中，展示了将权重从32bit变成1bit的二元后，存储量降低了32倍，计算量降低了2倍。
- 因为权重只有-1和+1，无需进行乘法运算，只需要执行加法操作，因此计算量降低2倍。

![lect6-14.webp](/upload/lect6-14.webp)

确定性二值化
- 基于阈值直接计算位值，通常阈值选0，从而得到一个符号函数。如下：

q = sign(r) = \left\{\begin{aligned} +1,r \geq 0 \\ -1,r < 0 \end{aligned} \right.

随机二值化
- 使用全局统计信息或输入数据的值来确定取值为-1或+1的概率。
- 较难实现，因为它需要硬件在量化时生成随机位。
- 比如：在Binary Connect（BC）中，概率是由hard sigmoid函数 \sigma(r) 决定的

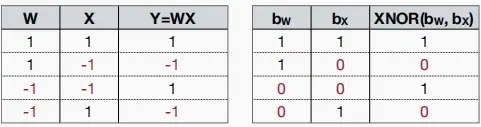
探讨一下二进制乘法和xor的区别
- 如下图表格，可以看出乘法和xor具有相似的规律。
- 因此二进制乘法和xor可以通过下列公式得到相同的结果。其中n是输入的数量，即结果=-输入数量+非零数量*2；非零数量即异或操作，可以映射到一个“popcount”的高效硬件操作上。
  
  y_i = -n + 2 * \sum_j w_{ij} :xnor : x_j
- 将输入和权重二值化后的效果：

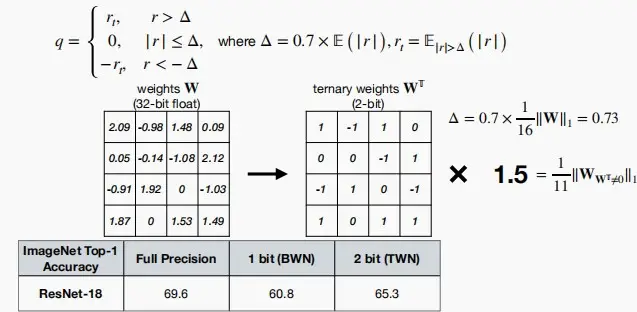
Ternary Weight Networks(TWN)三元权重网络

将权重量化为+1、-1和0。
设置一个阈值 \Delta = 0.7×E(|r|),r_t = E_{|r|>\Delta}(|r|)，按照图中的公式将权重量化为+1、-1和0。
可以看到三元权重网络TWN相比于二元权重网络BWN精度提高了4.5%。

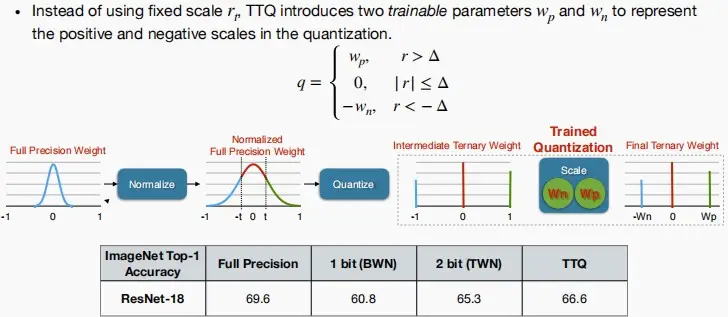
Trained Ternary Quantization (TTQ)可训练的三元量化

TTQ没有使用固定的尺度 r_t，而是引入了两个可训练的参数 w_p和w_n来表示量化过程中的正负尺度。
可以看到精度有小幅上升，实现精准微调。

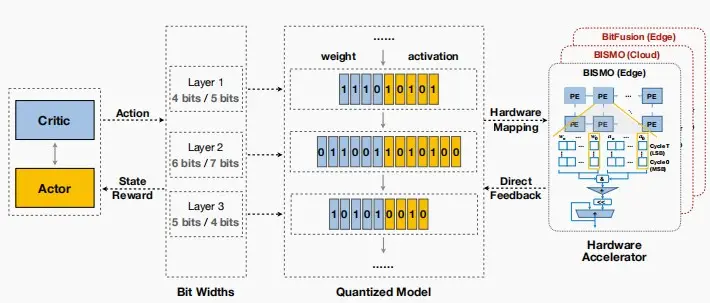
(Ⅵ) Mixed-Precision Quantization混合精度量化

就像不同层对剪枝的敏感不同，不同层对量化的敏感也不同，因此引入混合精度量化，为不同层设计不同的量化精度。
混合精度量化也代表着巨大的设计空间，可以使用自动化的设计方法-Iter Pritik，结合硬件映射图，直接收集反馈信息，包括延迟和能耗，以生成状态及奖励。随后，行动器自行学习以提出更佳的行动方案。

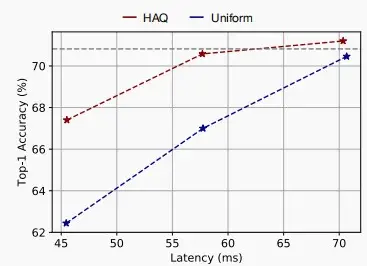
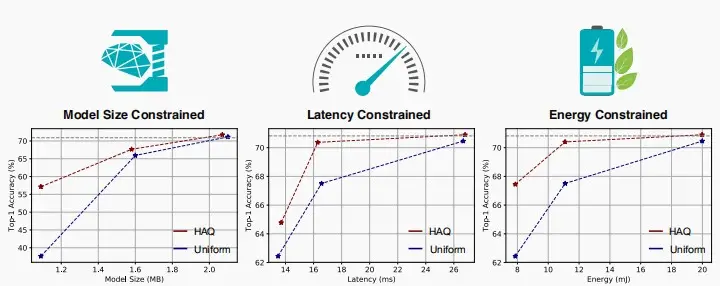
效果如下，对准确率、模型大小、延迟和能耗都有提升。

[MIT6.5940] Lect 5&6 Quantization