系列序言

本系列为MIT 6.5940的课程笔记，希望通过记录和总结来督促自己学习，同时也能分享技术知识。由于本人为大模型初学者，对于课程的理解也许有一定的误差，如有错误，欢迎评论区或其他联系方式交流讨论；如果觉得有帮助的话，你的点赞将给我带来坚持分享的动力。

Lect 1主要是介绍Han老师过去的优化工作，分别包含视觉模型、语言模型和多模型三种模型，通过剪枝、知识蒸馏等手段降低训练和推理成本，在保证性能的前提下，拥有更快的速度和更少的参数规模，使得其能够部署在边缘端。由于Lect 1主要是介绍，因此没有总结笔记，本系列直接从Lect 2开始。

课程地址：MIT 6.5940

课程意义

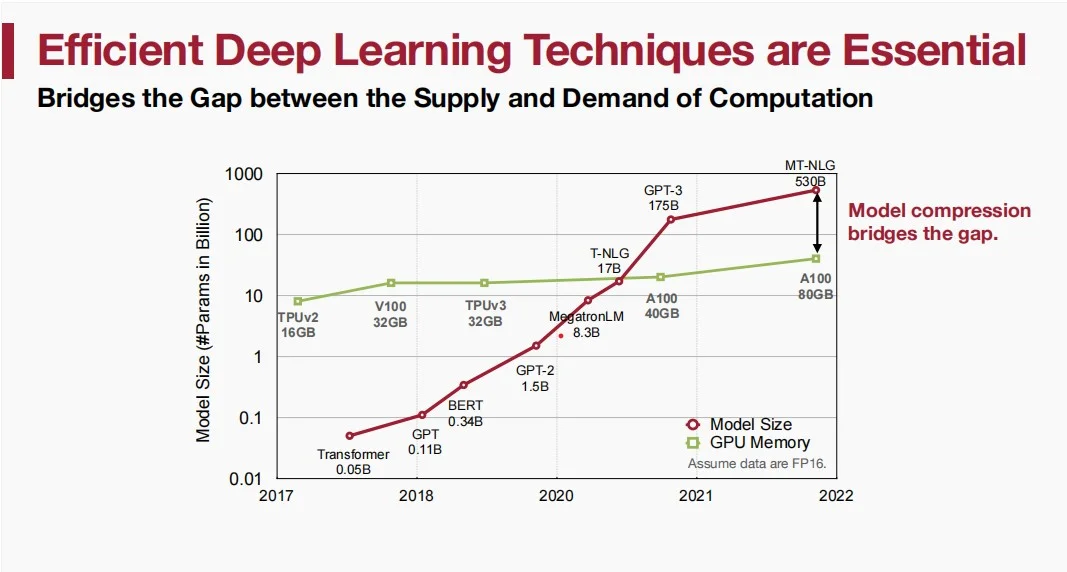
如图，即使GPU内存按照摩尔定律每两年翻一倍，但是大模型却按照每两年四倍的速度增长，显然我们需要模型压缩和高效AI的技术来弥合中间的差距。

Lect 2大纲

一、回顾神经网络的专业术语

神经元和突触（略）

深度神经网络

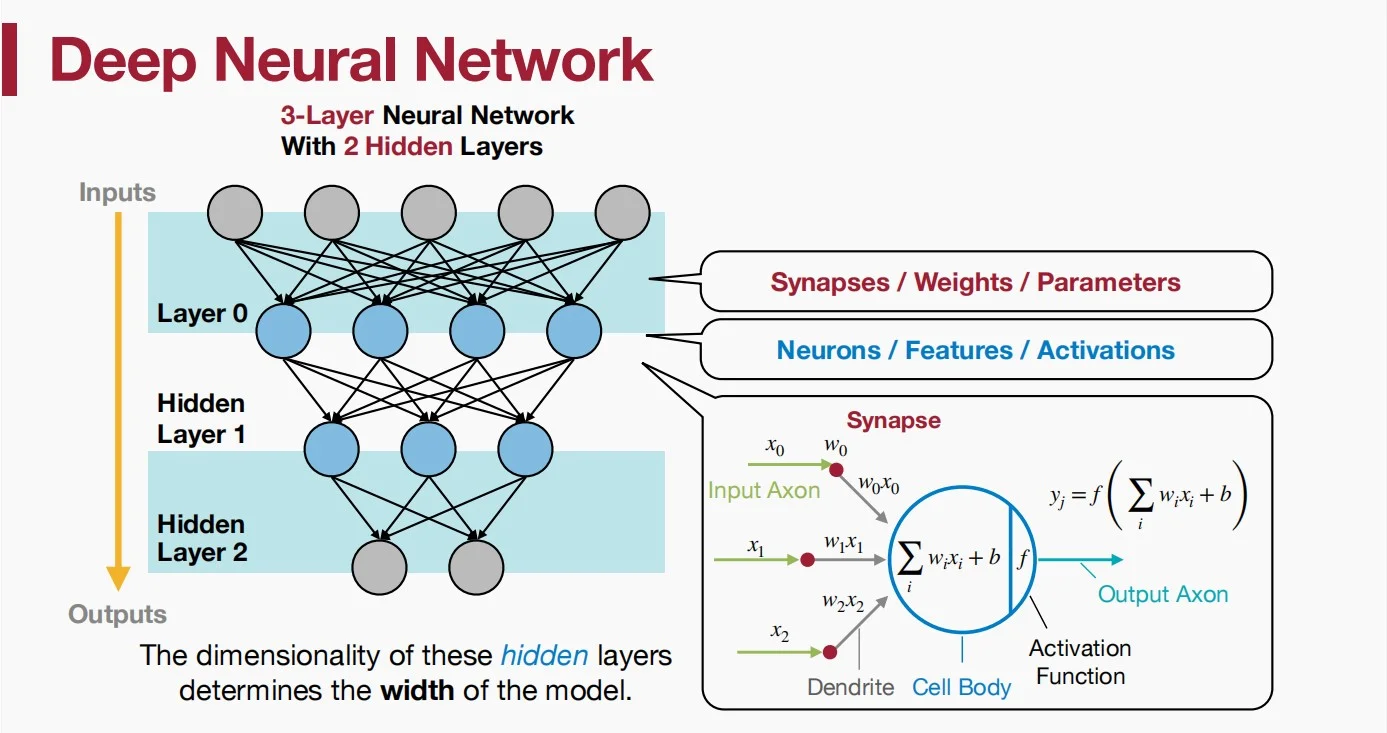
以下词汇在深度神经网络中表示同一概念：

Synapses突触 = Weights权重 = Parameters参数
Neurons神经元 = Features特征 = Activations激活

模型的宽度 = 隐藏维度的大小（每一层中神经元的数量）

模型的深度 = 隐藏层的数量

在参数数量和计算量相同的情况下，宽而浅和窄而深 的神经网络哪个在GPU上运行更快？

答案：宽而浅，因为每一层代表一次内核调用，浅的神经网络会更快。但是为了训练模型使其易于收敛并达到良好准确性，我们需要一个深度模型，因此需要权衡。在高准确度、易于训练、易于收敛，同时对硬件友好、具有高利用率、运行快等方面之间进行平衡。

二、回顾神经网络中的常用构建块

全连接层

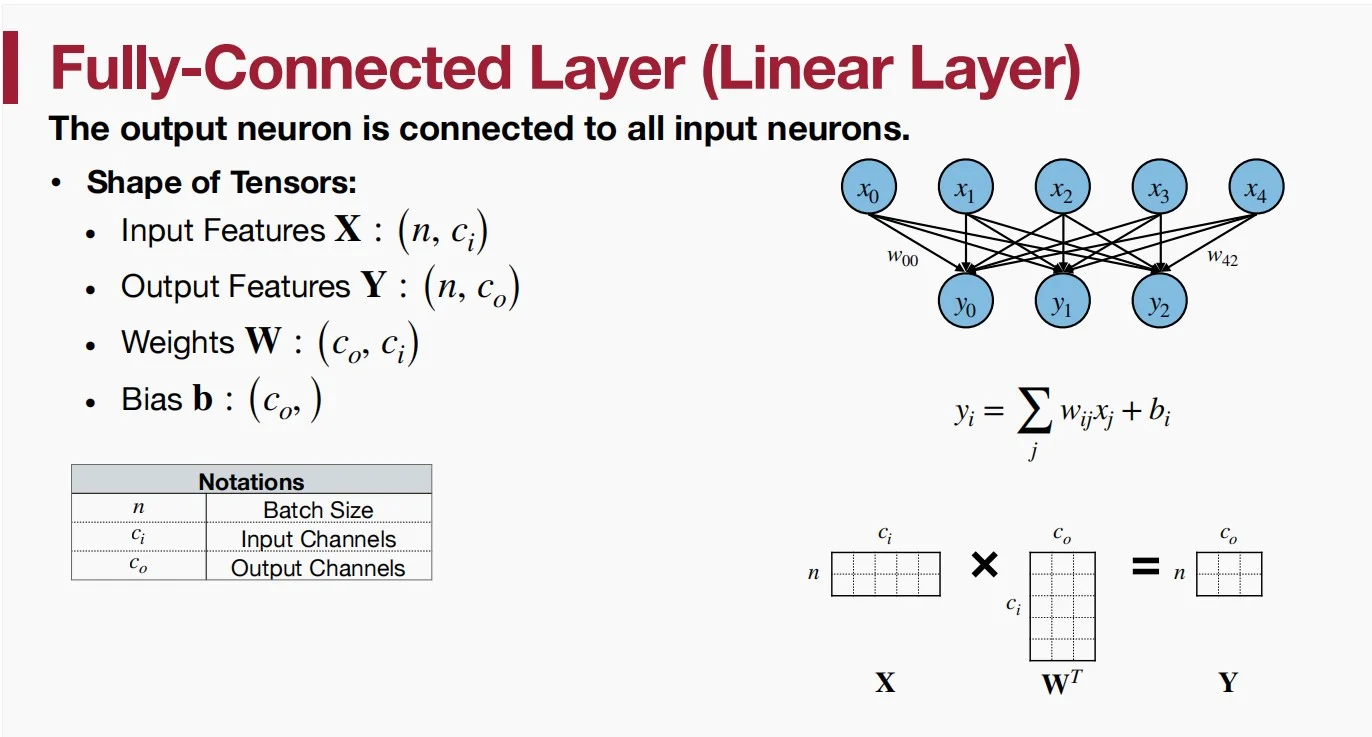
主要讲了输入、输出和权重的大小，以及运算。

卷积层

一维卷积（二维输入）

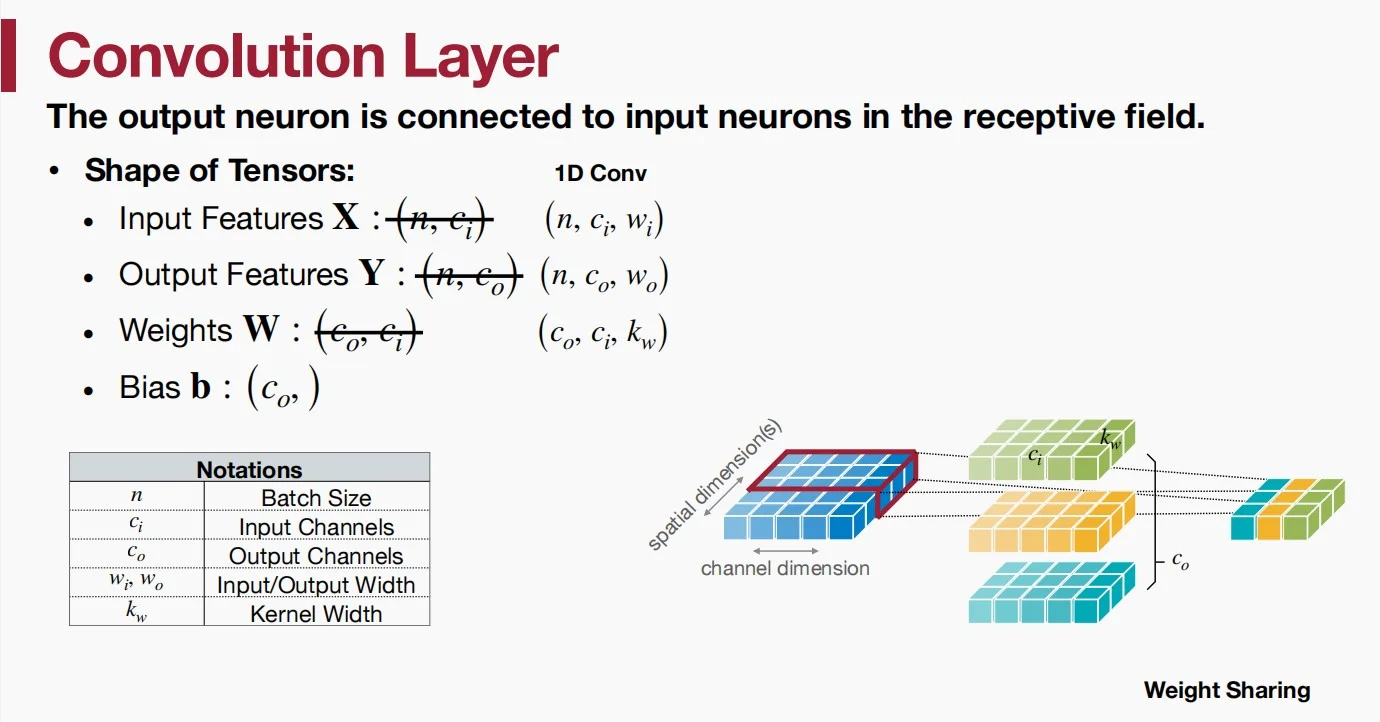
如图示例，输入特征为(1,5,5)，输出特征为(1,3,3)，权重为(3,5,3)。

二维卷积（三维输入）

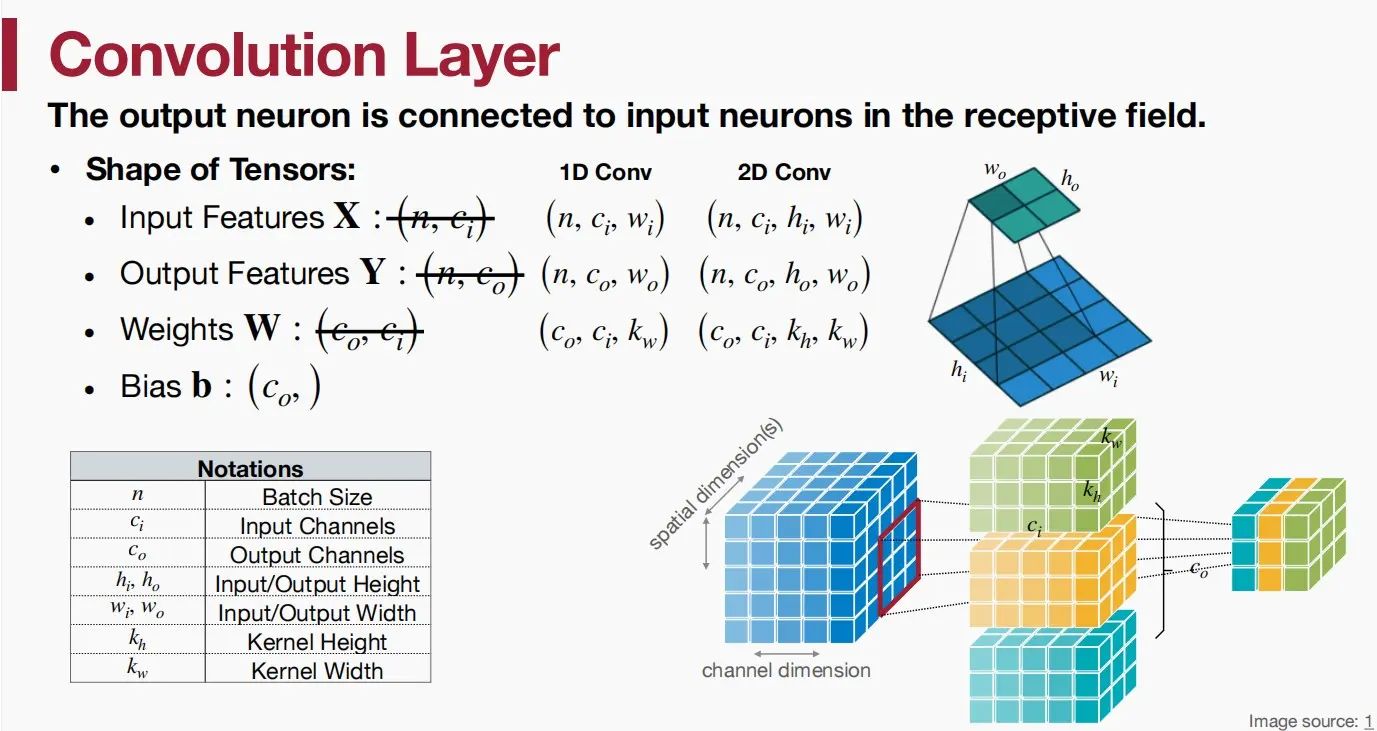
如图示例，输入特征为(1,5,5,5)，输出特征为（1,3,3,3），权重为（3,5,3,3）。

输入和输出的大小有什么联系？

答案：h_0 = h_i - k_h + 1或w_0 = w_i - k_w + 1，如一维卷积图中w_i=5，k_w = 3，w_0 = 3，二维卷积图中h_i=5，k_h = 3，h_0 = 3。

为了保持特征图的尺寸，引入了填充padding，使得输入与输出保持尺寸一致。填充方法包含零填充、反射填充和复制填充。PyTorch中默认最常见的零填充。

感受野

什么是感受野？一个特定位置的输出值受到输入的哪些位置的影响。

感受野大小取决于其所处的卷积层的卷积核大小和步幅，以及之前卷积层的感受野大小。通过堆叠多个卷积层，神经网络可以逐渐扩大感受野，从而更好地捕捉输入数据的全局特征。较大的感受野可以帮助神经网络理解更广阔范围的上下文信息，并提高对复杂模式和结构的识别能力。

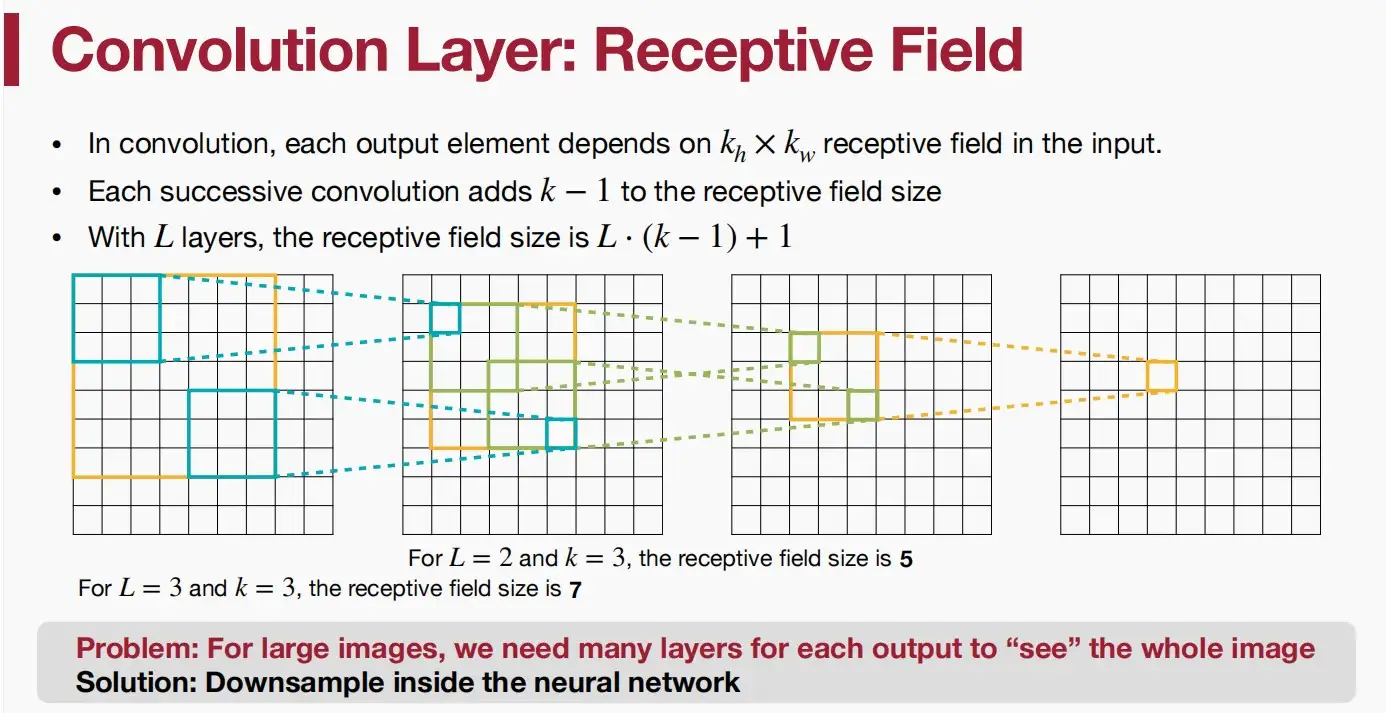
在卷积中，每个输出像素取决于输入中k_h*k_w的感受野（即卷积核大小）。
每个连续的卷积都会增加k-1大小的感受野的。
第L层的某个像素，对应于初始输入的感受野大小为L*(k-1)+1。

如图中示例，输出中每个像素取决于输入的3*3感受野；k=3，每个连续的卷积增加大小为2的感受野；对于L=3层中的像素感受野为3*(3-1)+1=7，对于L = 2层中的像素感受野为2*(3-1)+1=5。

问题：对于大图像，我们需要许多层来感受整个图像（层数多计算慢，卷积核大参数多->运行开销大）
解决：Downsample下采样，包括：增大步长、池化等。

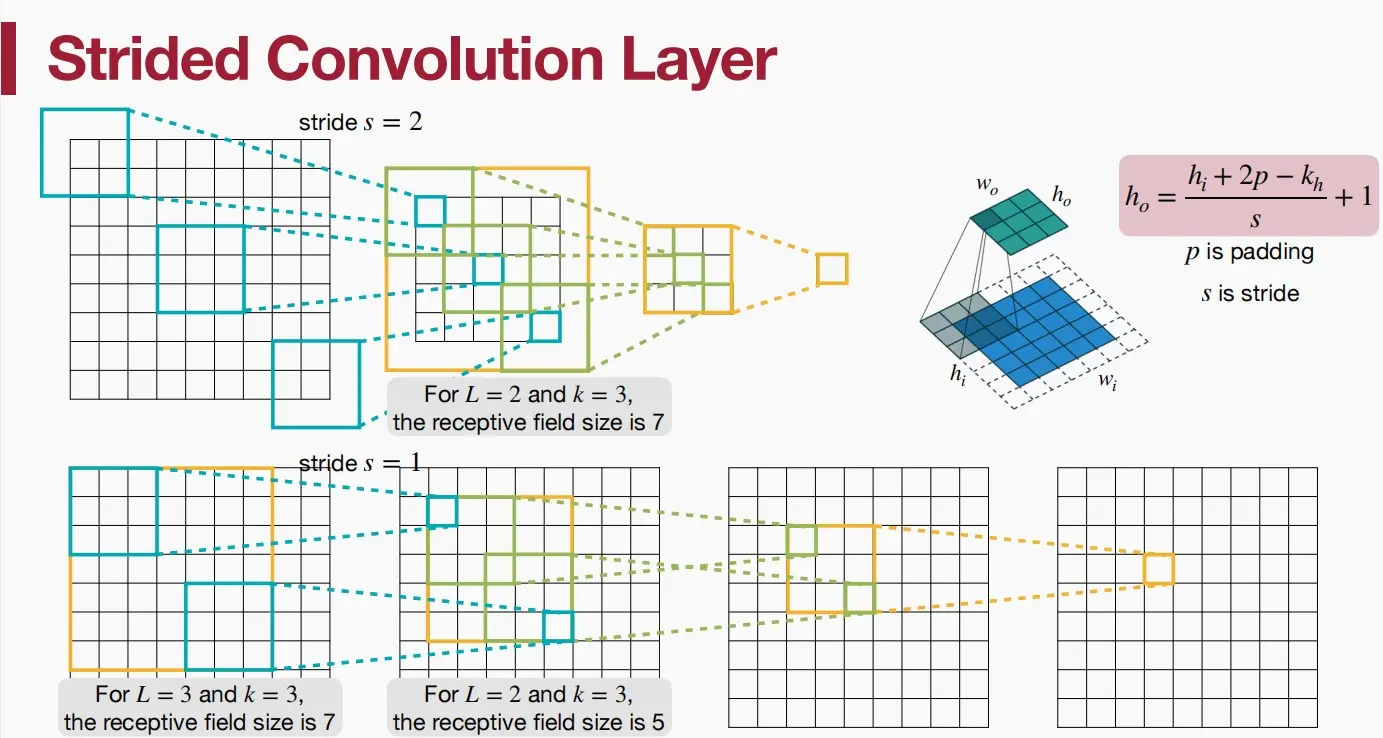
如图通过增大步长p为2，保持卷积核大小k=3不变，同样使得感受野大小为7，只需要两层即可。
此时输入和输出的大小关系变为：

h_0 = (h_i + 2p - k_h) / s + 1

分组卷积

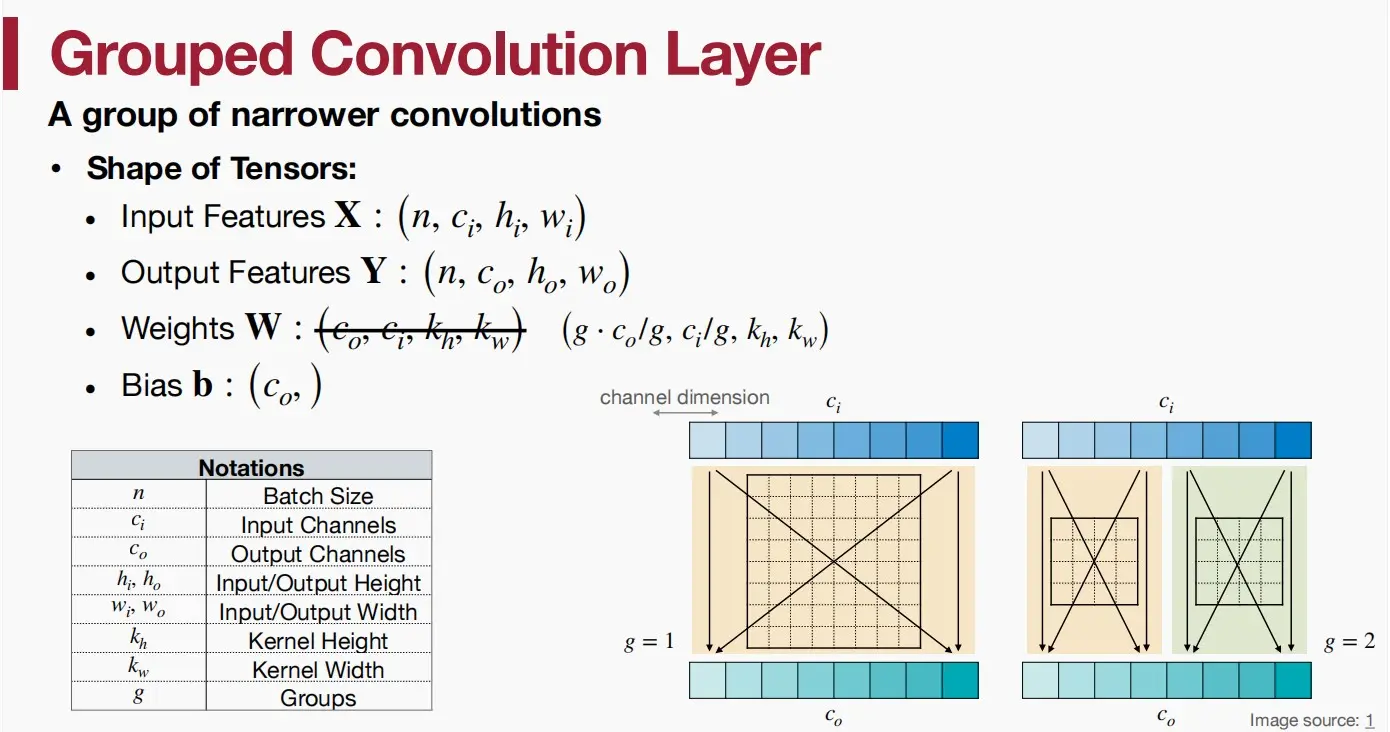
分组卷积层通过将输入通道分成多个组，并为每个组分配一组独立的卷积核来解决这个问题。每个组的输入通道仅与相应组的卷积核进行卷积操作，生成一组输出特征图。最后，所有组的输出特征图被连接在一起，形成最终的输出。这种分组方法可以减少卷积层的参数量，加速计算，并提高网络的效率。

观察上图中的参数可以看到，输入和输出特征没有变化，而参数W的数量减少了g倍。如下图可以直观的看到同样大小的输入特征和参数，得到了不同大小的输出特征，意味着通过分组卷积能够编码更多的信息。关于分组卷积的详细解释，可以参考这篇文章。

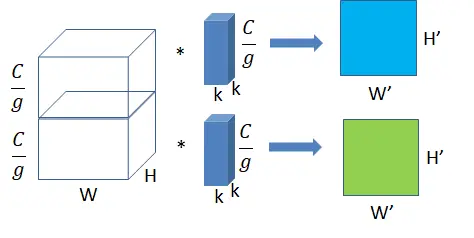
深度分离卷积

深度分离卷积是分组卷积的一种特殊形式，其分组数g = C，其中是输入特征的通道数。此时权重效率大幅增加，参数数量急剧减小，且特征保持不变。深度分离卷积是MobileNet家族的基础，然而这种设计并非十分高效。为了弥补减少权重参数导致的网络表达能力，MobileNetV2中的深度卷积层之后的激活通道数量增加了6倍，以引入更多的非线性变换。增加通道数量会导致大量内存移动，数据移动的成本较高。**

池化层

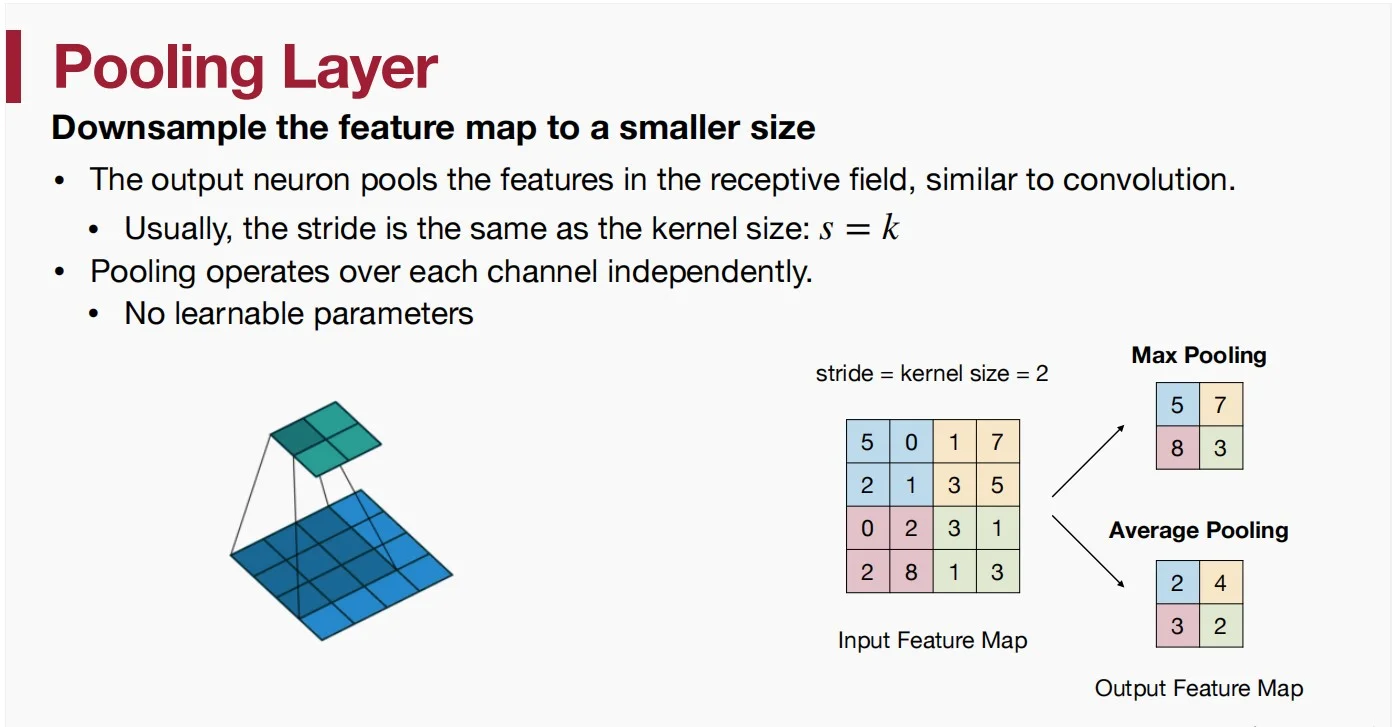
常见池化方法：平均、最大、求和......
优点：0学习参数
缺点：较小的容量和表达能力

归一层

在神经网络中对输入数据进行标准化处理，即将数据化为均值为0，方差为1。归一化层可以帮助加速训练过程、提高网络的稳定性和泛化能力。通过下列公式进行归一处理，其中\mu为均值，\sigma为标准差。

\hat{x_i} = (x_i - \mu_i) / \sigma

通常分为下列四种：

批量归一化（Batch Normalization）是一种在训练过程中对每个小批量样本的特征进行归一化的方法。它在每个批次内计算特征的均值和标准差，并将特征进行线性变换。
层归一化（Layer Normalization）是一种对单个样本的特征进行归一化的方法，与批量归一化不同，它在每个样本内计算特征的均值和标准差，并进行相应的归一化处理。层归一化通常用于递归神经网络（RNN）或卷积神经网络（CNN）等不适合使用批量归一化的场景。
实例归一化（Instance Normalization）是一种归一化的方法，它在每个样本内对特征进行归一化处理。与批量归一化和层归一化不同，实例归一化不针对小批量或整个层的数据进行归一化，而是针对每个样本的特征进行独立归一化。
组归一化（Group Normalization）是一种在通道维度上对特征进行归一化的方法。它将通道分成若干个组，并对每个组内的特征进行归一化。组归一化的主要优点是对小批量数据和小尺寸的输入数据具有较好的表现，相对于批量归一化更适用于较小的模型或具有较少样本的情况。
在进行大模型微调时，一种非常经济高效的方法实际上只是微调批量归一化或层归一化中的缩放因子和偏差。

激活函数

大部分激活函数都对硬件不友好，如果有必要，应该谨慎选择对硬件不友好的激活函数。

Transformer

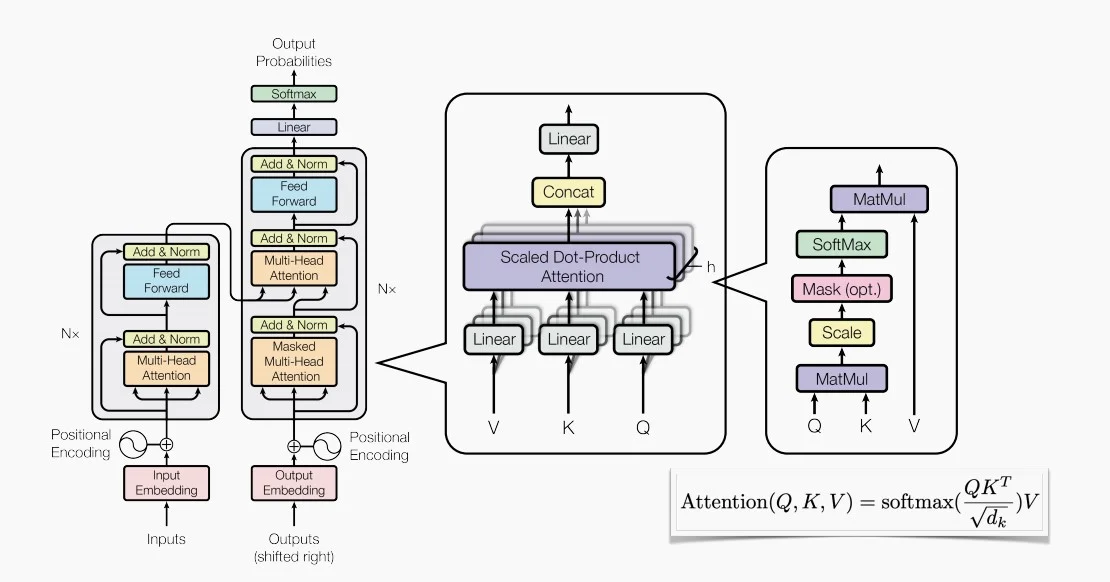
三、回顾卷积神经网络的架构

本小节主要是快速介绍各种架构的每一层的选择和设计，没有细讲，包括：AlexNet, VGG-16, ResNet-50, MobileNetV2。此处略过。

四、介绍流行的神经网络的效率指标

如何衡量神经网络的效率

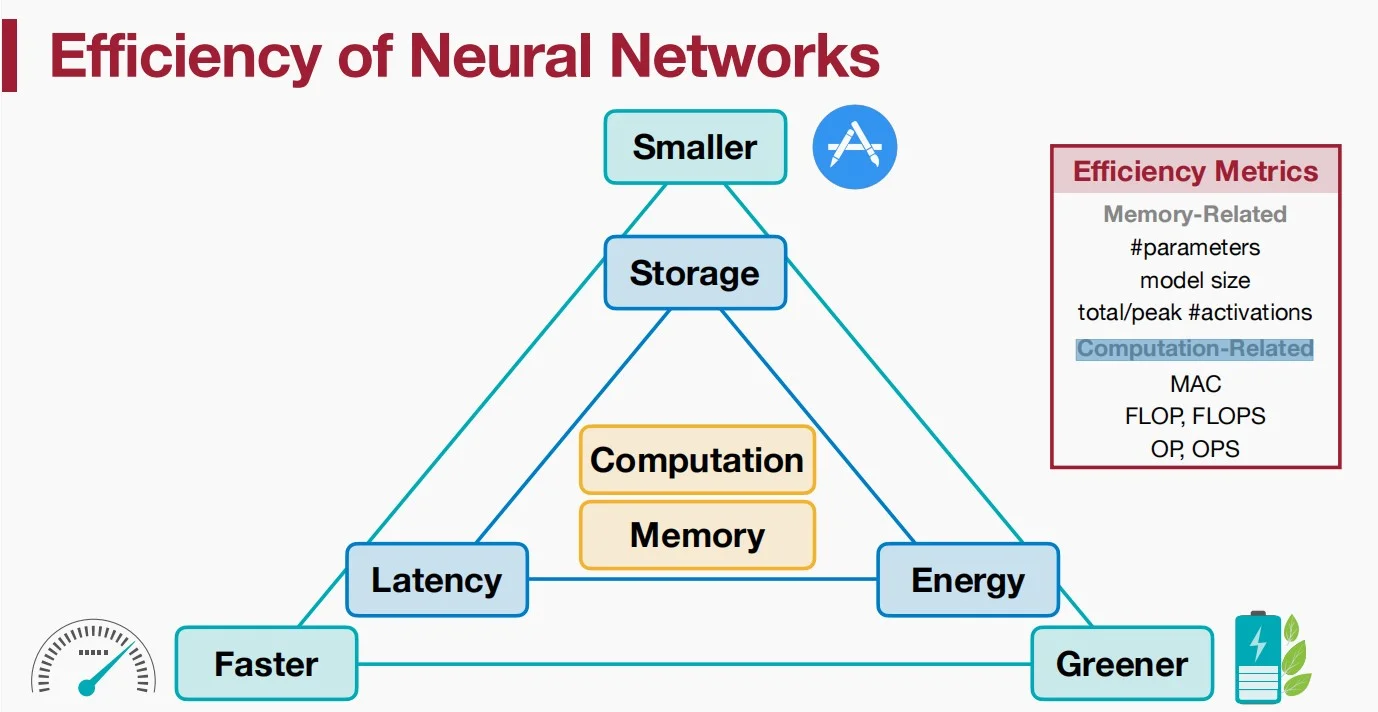
从三个方面：延迟、存储和能耗，一个模型很难同时在三个方面都取得最佳的效果，往往需要做出权衡。接下来计算具体的指标。

延迟

延迟衡量的时特定任务的延迟时间。例如：图像识别中每张图片的处理时间，视频目标检测中每一帧的处理时间。

吞吐量

吞吐量衡量的是数据处理的速度。例如：视频理解模型中每秒处理的视频数量。

1 延迟和吞吐量的关系？
图像识别任务中，处理每张图像的时间是延迟，每秒处理的图像数量是吞吐量。
2 延迟越低，吞吐量越高吗？吞吐量越高，延迟越高吗？
否，两者并不相互转化。可以通过批处理来实现a比b更高的吞吐量，但是延迟也更高。

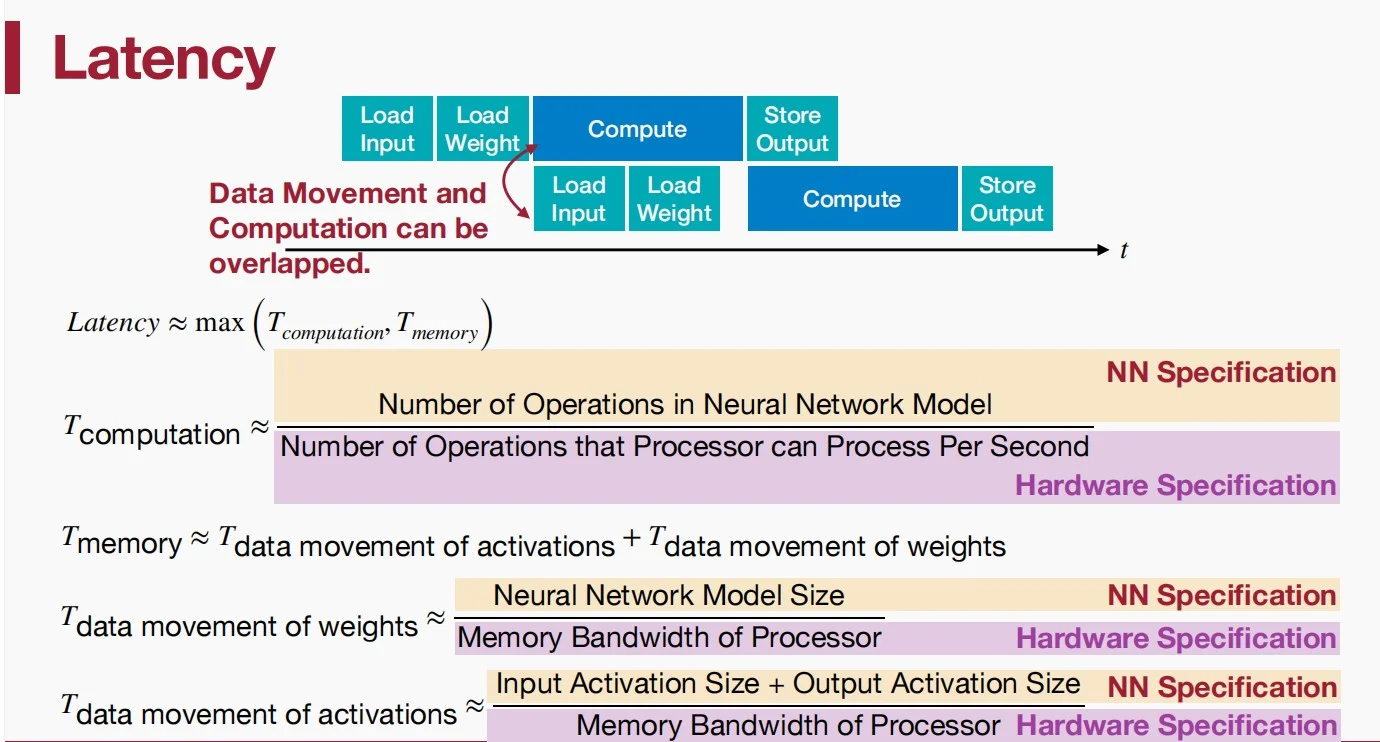
延迟往往是更加棘手的问题，因此得到了更多的关注。通过重叠计算和内存访问，是降低延迟的有效方法。即通过流水线式处理，使得数据移动和处理产生重叠（指不同层之间），降低延迟。
如图，延迟分为计算部分和内存部分。“NN Specification”指针对特定神经网络，“Hardware Specification”是指针对特定硬件。Lantecy往往被计算或内存其中一个所限制。

能源消耗

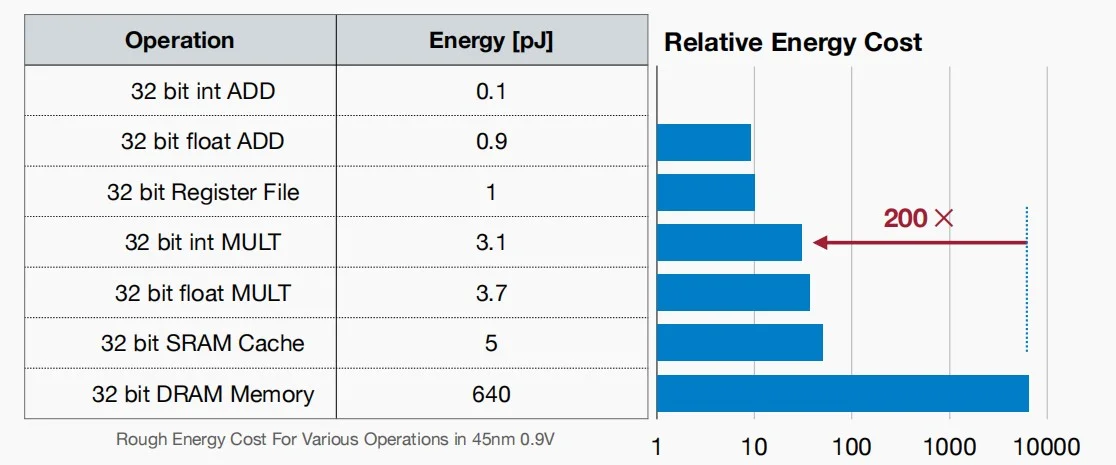
如图中各种操作的能耗可以看出，内存引用的成本比算数运算高出非常多。而数据移动导致内存引用，因此应该尽力减少数据移动，降低成本。

参数数量

各种层的参数计算方法
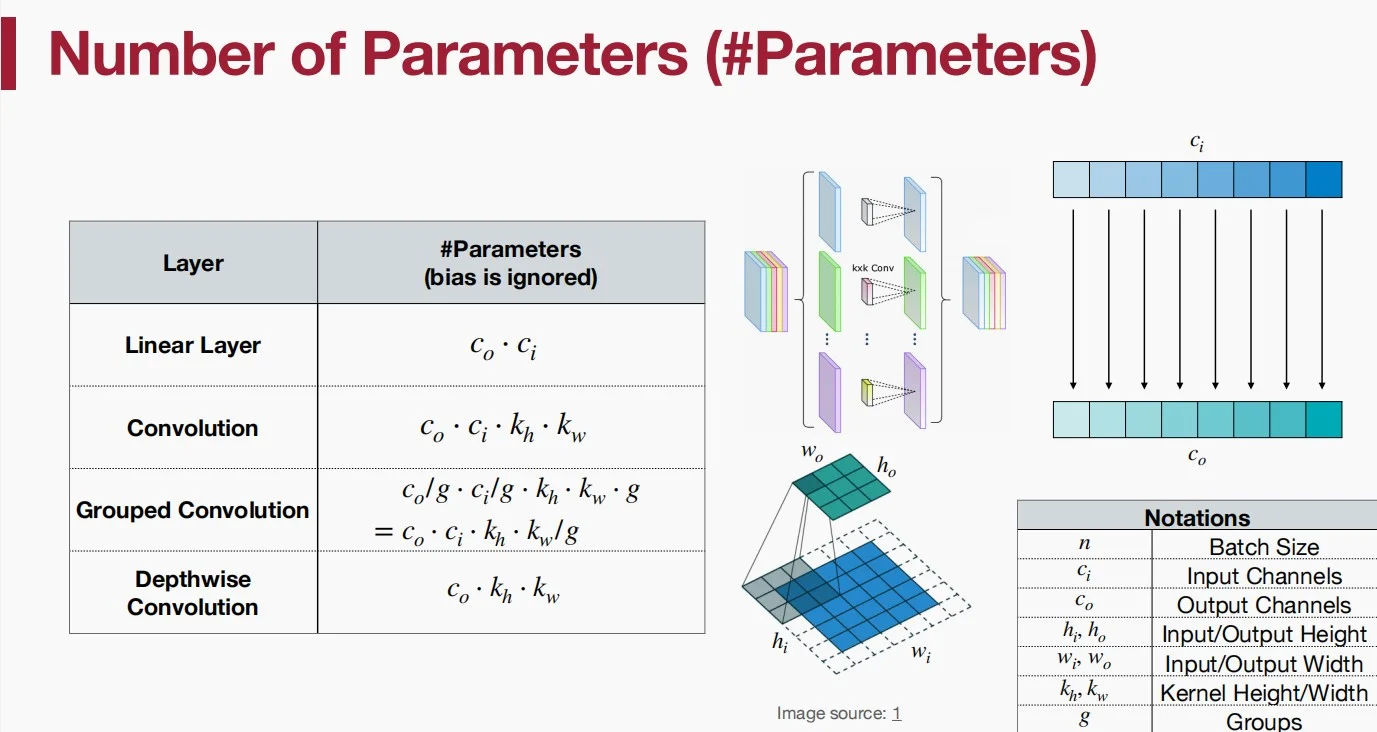
AlexNet

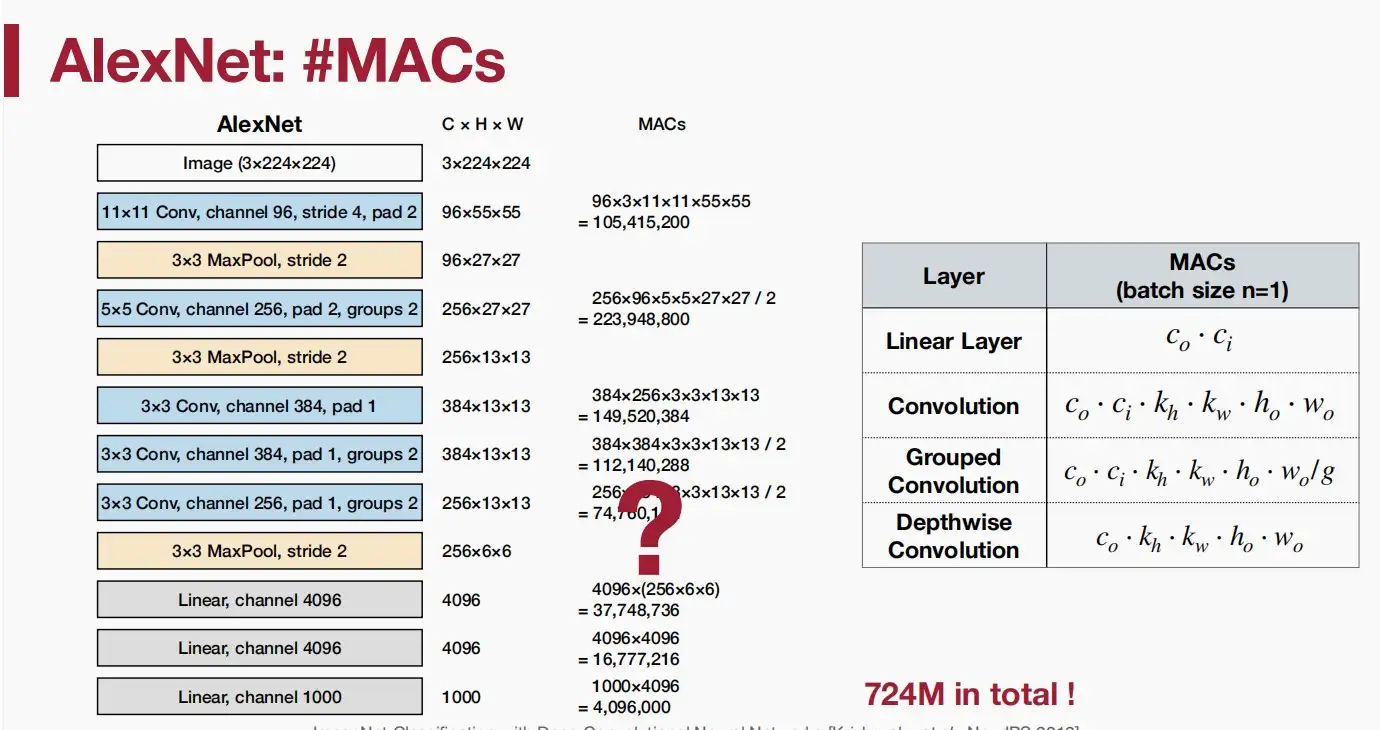可以轻松的算出各层参数数量，显然全连接层的参数数量远超其他层。因此在后来的CNN模型中摒弃了全连接层，然而Transformer模型又使用了非常多的全连接层，以此提供足够的表达能力。

模型大小

模型大小往往使用参数数量来计算。

位宽 = 每个参数需要多少位表示。
模型大小 = 位宽 * 参数数量

激活数

从ResNet到MobileNetV2参数数量大幅减小，但是峰值激活却有所增加。而如果设备无法容纳峰值激活内存的大小，峰值激活将成为了真正的瓶颈所在。

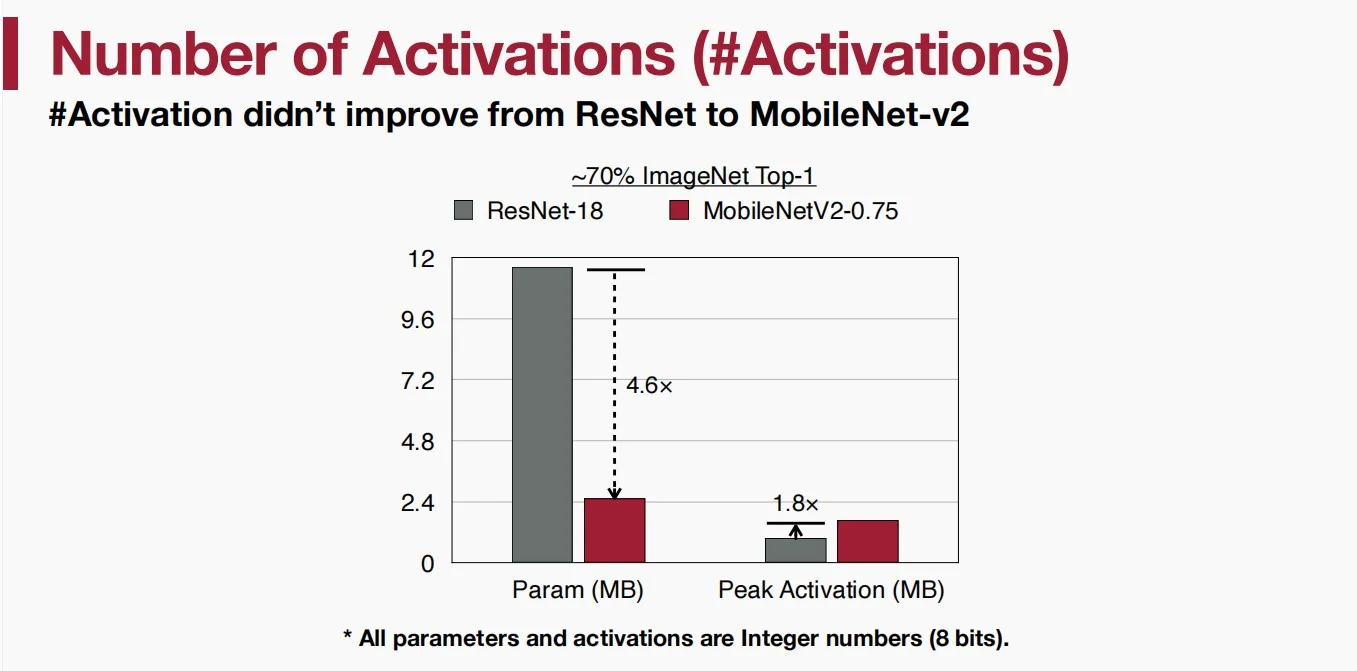
如图可以观察到对于CNNs权重与激活呈现U型。因为在早期分辨率较高，拥有大量的激活权重。随着后期分辨率降低，而通道数大幅增加导致权重内存升高。

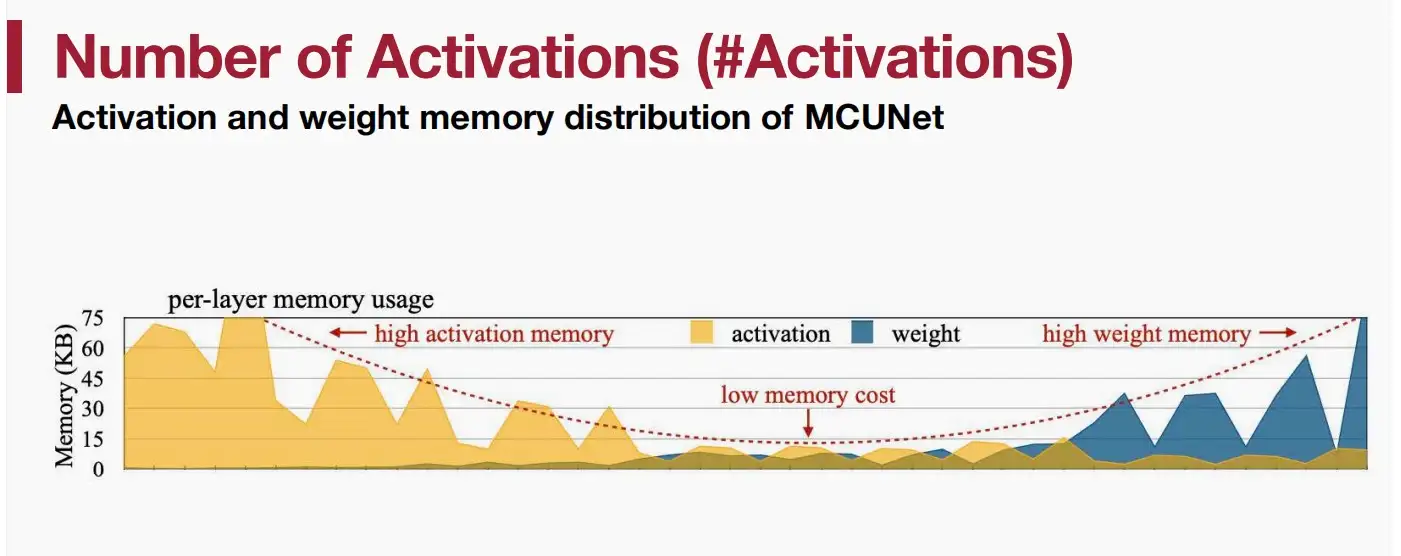
MACs乘累加运算

MAC指Multiply-Accumulate operation，即乘累加运算 a+b*c 为一次乘累加运算
对于矩阵向量乘法，MACs=m∗n，即长宽
对于一般的矩阵-矩阵乘法，MACs=m∗n∗k

由此，我们可以得到各层的MACs，注意下图中batch size n = 1。

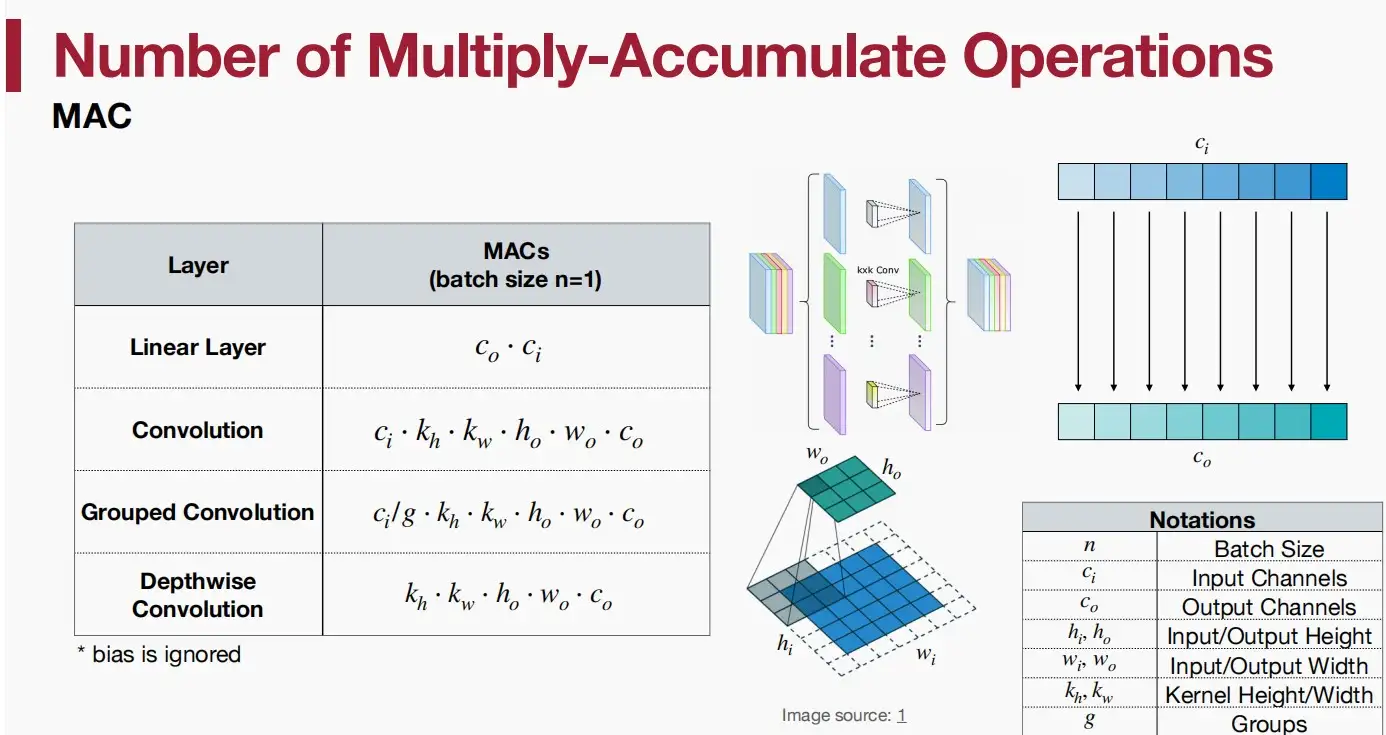
通过AlexNet的结构和大小可以得到，AlexNet的总MACs为724M。

运算次数Number of Operations

浮点数运算Floating Point Operations (FLOP)
- 浮点数加法和浮点数乘法都属于FLOP，因此一次乘累加MAC运算 = 两次FLOP
- 因此，AlexNet有724M MACs，浮点数运算的总数将为724M×2 = 1.4G FLOPs
- 每秒浮点数运算 Floating Point Operation Per Second (FLOPS)
- FLOPS=FLOPs/second
运算Operations (OP)
- 神经网络计算中的激活/权值并不总是浮点数，因此引入了number of operations操作次数，包括整数和浮点数运算。
- 同样的也有，每秒运算Operation Per Second (OPS)
- OPS=OPs/second

五、思考总结

这节课主要是回顾了很多课程需要的前置知识，但是仍然学到了很多新东西，这也代表自己的基础有待提高，在接下来的课程里需要不断的补漏。

这么课最印象深刻的词就是“trade-off”，没有完美的解决方案，只有不断改进的模型。科研就是一个不断试错的过程，找到更优的方案就是一种进步。表达空间需要参数，而参数带来更大的内存压力和能耗，因此需要去平衡各种效率指标。AI走向边缘端是必然的趋势，而如今GPU的成本、能耗和体积都不足以支撑大量部署在边缘端，实现这一趋势目前看最有可能的或许是对AI进行优化压缩，这也是这门课的核心技术。

[MIT6.5940] Lect 2 - Basics of Neural Networks