论文笔记《Feature Alignment and Uniformity for Test Time Adaptation》

论文笔记《Feature Alignment and Uniformity for Test Time Adaptation》

Administrator 100 2025-04-21

摘要

  • 本文工作

    • 作者首先将 TTA 视为一个特征修正问题，这是由于源域和目标域之间的领域差距所导致的。在此基础上，遵循 对齐 和 一致性 两个指标来讨论测试时的特征修正。
      • 测试时特征一致性：作者提出了一种 测试时自蒸馏策略，以确保当前批次与所有先前批次的表示之间的一致性。
      • 测试时特征对齐：我们提出了一种 基于记忆的空间局部聚类策略，通过对即将到来的批次中的邻域样本进行表示对齐。
    • 为了应对常见的噪声标签问题，作者设计了 熵过滤器 和 一致性过滤器 来选择并丢弃可能的噪声标签。

1 引言

  • TTA -> 特征修正问题

    • 在 TTA 的测试阶段，模型已经学习了针对源域的特征表示，但由于源域和目标域之间的巨大差距，模型可能为目标域生成不准确的表示。因此，有必要对目标域的特征表示进行修正。
    • 为了为目标域获得更好的表示，我们利用了常用的表示质量评估指标，这些指标可以归结为：
      • 一致性（Uniformity） ：不同类别的图像应在潜在空间中尽可能均匀分布。
      • 对齐（Alignment） ：相似的图像应具有相似的表示。

  • 现有工作

    • 大多数关于 TTA 的先前工作都可以从所提出的表示修正视角进行归纳。
    • 一些方法通过执行特征对齐过程来调整源模型，例如 特征匹配 和 预测调整 。其中一种代表性方法是 LAME ，它利用拉普拉斯调整的最大似然估计，鼓励特征空间中的邻域样本具有相似的预测结果。
    • 另一些方法使目标域特征在特征空间中更加均匀分布，包括 熵最小化 、原型调整 、信息最大化 以及 批归一化统计对齐 。其中一个代表性方法是 T3A ，它通过构建支持集调整原型（类别中心），以获得更均匀的表示。
    • 局限：然而，现有方法都没有同时从 表示对齐 和 表示一致性 两个角度解决 TTA 问题。

  • 测试时特征一致性

    • 目标：希望来自不同类别的测试图像的表示能够在潜在空间中尽可能均匀分布。
    • 困难：TTA设置下，只能以在线方式访问有限的测试样本。
    • 解决办法 - 测试时自蒸馏 TSD
      • 作者构建了一个 记忆库，用于存储所有到达样本的特征表示和 logits，从而保留来自先前数据的有用信息。利用记忆库中的 logits 和特征计算 每个类别的伪原型。
      • 然后，为了保证当前批次样本的一致性，基于原型分类的预测分布与模型预测（线性分类器的输出）应尽可能相似，即当前批次某类图像的特征分布应与之前所有同类别图像的特征分布保持一致。
      • 受此启发，作者 最小化线性分类器和基于原型分类器输出之间的距离。这种模式类似于 自蒸馏，即在同一网络架构的不同层之间传递知识。然而，与典型的自蒸馏不同，本文方法不需要任何真实标签的监督。

  • 测试时特征对齐

    • 目标：让同一类别的图像在潜在空间中具有相似的特征表示。
    • 困难：TTA设置下，由于领域差距，源模型生成的伪标签可能存在噪声。
    • 解决办法 - 记忆化的空间局部聚类 MSLC
      • 提出了一种 K近邻特征对齐（K-nearest feature alignment） 方法，鼓励同一类别的特征彼此靠近，或不同类别的特征彼此远离。
      • 具体而言，从记忆库中检索即将到来图像的 K 近邻特征，并在图像的表示和 logits 之间添加 一致性正则化。

  • 熵过滤器与一致性过滤器

    • 动机：尽管采取了上述措施，噪声标签问题仍无法完全缓解。

    • 为了进一步减少噪声标签的影响，我们采用了 熵过滤器（Entropy Filter） 和 一致性过滤器（Consistency Filter） 来过滤噪声标签，从而提升性能。

      • 熵过滤器：在计算原型时，过滤掉高熵的噪声特征，因为不可靠样本通常会产生较高的熵。
      • 一致性过滤器：对于可靠样本，基于原型分类器和线性分类器的预测结果理论上应该是一致的。

2 方法

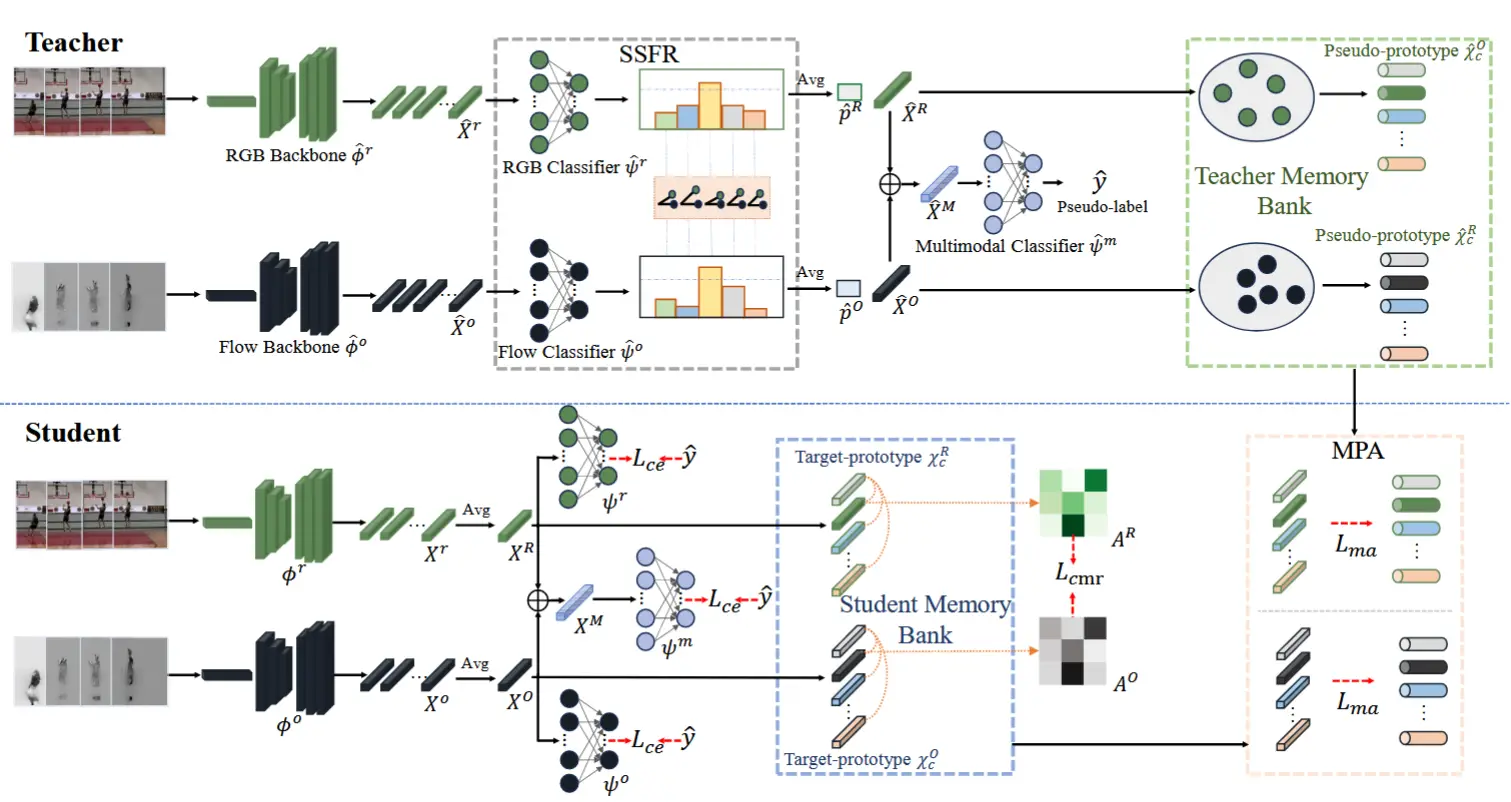
图1为本文方法的整体流程。

paper35-1.webp


2.1 预备知识

在 TTA 中，只能以在线方式访问目标域的无标签图像和在源域上预训练的模型。给定在源域 ​\mathcal{D}_s 上训练的模型，我们的目标是使用目标域的无标签数据 ​\{x_i\} \in \mathcal{D}_t, i \in \{1...N\} 对模型进行调整，其中 ​x_i 表示目标域 ​\mathcal{D}_t 的第 ​i 张图像，​N 表示目标图像的数量，​\mathcal{D}_s 表示源域。在测试阶段，我们将模型初始化为 ​g = f \circ h，其中 ​f 表示主干网络，​h 表示线性分类头。对于图像 ​x_i，模型 ​g 的输出表示为 ​p_i = g(x_i) \in \mathbb{R}^C，其中 ​C 表示类别数量。


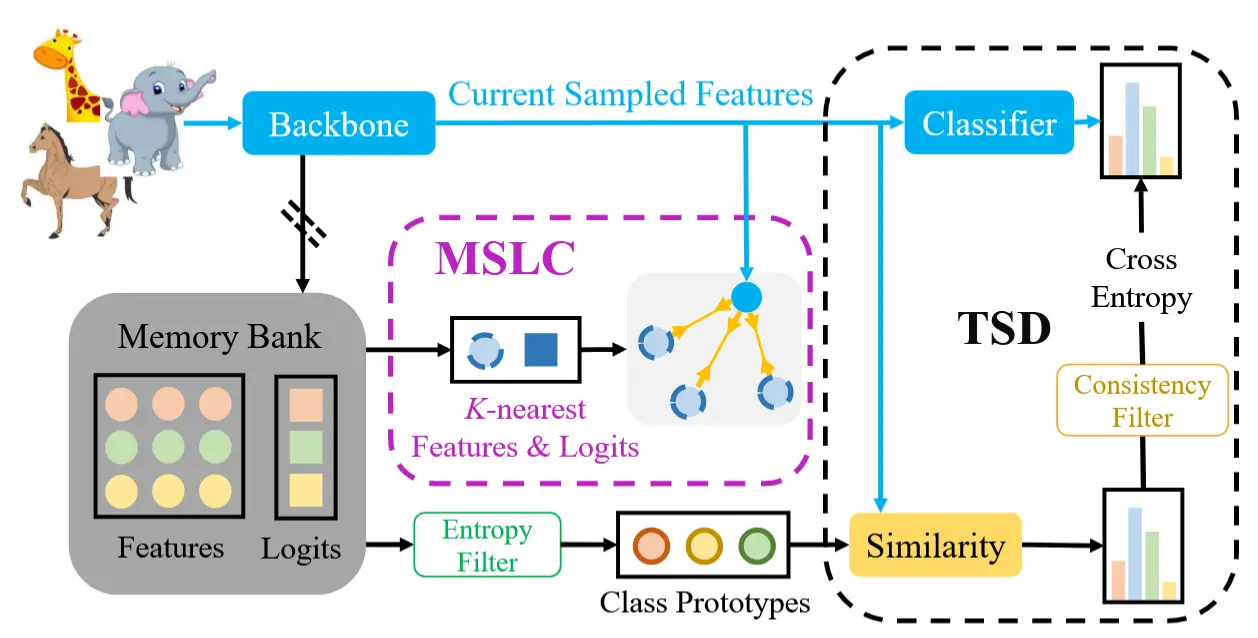
2.2 测试时自蒸馏 (TSD)

在自适应过程中，给定一批无标签的测试样本，我们可以通过预训练模型生成 图像嵌入 ​z_i = f(x_i)、logits ​p_i = h(z_i) 和 伪标签 ​\hat{y}_i = \arg\max p_i。

（记忆库） 然后，我们维护一个记忆库 ​\mathcal{B} = \{(z_i, p_i)\} 来 存储图像嵌入 ​z_i 和 logits ​p_i。根据 T3A [22] 的方法，记忆库初始化为线性分类器的权重。 当目标样本 ​x_i 到来时，对于每张图像，我们将图像嵌入 ​z_i 和 logits ​p_i 添加到记忆库中。为了建立当前样本与所有先前样本之间的关系，需要为每个类别生成伪原型。类 ​k 的原型可以公式化为：

c_k = \frac{\sum_i z_i \mathbb{1}[\hat{y}_i = k]}{\sum_i \mathbb{1}[\hat{y}_i = k]}, \tag{1}

其中 ​\mathbb{1}(\cdot) 是指示函数。

（香农熵过滤） 然而，一些伪标签可能被错误地分配到错误的类别，从而导致不正确的原型计算。为此，我们使用 香农熵 过滤噪声标签。对于预测 ​p_i，其熵可以计算为 ​H(p_i) = -\sum \sigma(p_i) \log \sigma(p_i)，其中 ​\sigma 表示 softmax 操作。我们的目标是过滤掉具有高熵的不可靠特征或预测，因为较低的熵通常意味着更高的准确性。具体而言，对于每个类别，在记忆库中具有最高熵的前 ​M 个图像嵌入将被忽略。之后，我们使用过滤后的嵌入计算原型（如公式 (1) 所示），并将 基于原型的分类输出 定义为特征与类别 ​k 的原型之间的 相似度的 softmax 值：

y_i^k = \frac{\exp\left(\text{sim}(z_i, c_k)\right)}{\sum_{k'=1}^C \exp\left(\text{sim}(z_i, c_{k'})\right)}, \tag{2}

其中 ​\text{sim}(z_i, c_k) 表示 ​z_i 和 ​c_k 之间的余弦相似度。


（预测一致性损失） 基于原型的分类结果 ​y_i 和网络 ​g 的输出 ​p_i 对于相同的输入应具有相似的分布。因此，为了保持一致性，我们提出了以下损失函数：

\mathcal{L}_i(p_i, y_i) = -\sigma(p_i) \log y_i. \tag{3}

需要注意的是，​p_i 是一个 软伪标签（soft pseudo label）。使用软标签的原因是软标签通常提供更多的信息 。通过提出的测试时自蒸馏方法，网络可以将当前样本的一致性映射到表示质量的提升上。

（预测一致性过滤） 尽管我们在计算原型时使用了熵过滤器来去除噪声标签，但仍然不可避免地会出现一些错误预测。对于可靠的样本，线性全连接层和基于原型的分类器的输出应该相似。因此，我们 采用一致性过滤器来识别错误预测。具体而言，如果线性分类器和基于原型的分类器产生相同的预测，即对 logits 执行 ​\arg\max 后得到相同的结果，则我们认为该样本是可靠的。这种策略可以通过为图像 ​x_i 使用过滤掩码实现，公式如下：

\mathcal{M}_i = \mathbb{1}[\arg\max p_i = \arg\max y_i]. \tag{4}

通过进行一致性过滤，我们可以 进一步过滤掉不可靠的样本，无监督自蒸馏损失可以公式化为：

\mathcal{L}_{tsd} = \frac{\sum_i \mathcal{L}_i * \mathcal{M}_i}{\sum_i \mathcal{M}_i}. \tag{5}

2.3 .记忆空间局部聚类 (MSLC)

本文鼓励K近邻特征而不是所有的特征都接近，以减少噪声标签的影响。一个简单的策略是在一批样本内加入一致性正则化。然而，历史时序信息被忽略，对齐效果较差。此外，存在一个平凡的解，如果我们只使用一个批量样本进行对齐，该模型可以很容易地将所有图像映射到某个类中。

为了解决这些问题，我们 将空间局部聚类与记忆库结合。我们首先 从记忆库中检索图像 ​x 的 ​K-近邻特征。根据我们的假设，图像 ​x 的 logits 应该与其最近邻在潜在空间中的 logits 对齐。为了实现这一点，我们 根据图像 ​x 和其邻居的嵌入之间的距离对两种 logits 进行对齐。公式如下：

\mathcal{L}_{mslc} = \frac{1}{K} \sum_{j=1}^K \text{sim}(z, z_j) (\sigma(p) - \sigma(p_j))^2, \tag{6}

其中 ​\text{sim}(z, z_j) 表示 ​z 和 ​z_j 之间的余弦相似度。​\{z_j\}_{j=1}^K 表示记忆库 ​\mathcal{B} 中 ​z 的 ​K-近邻图像嵌入，而 ​p_j 表示对应的 logits。如果 ​z_j 和 ​z 在特征空间中接近，即 ​\text{sim}(z, z_j) 较大，则该目标函数会促使 ​p_j 和 ​p 更加接近。我们断开 ​\text{sim}(z, z_j) 的梯度，即将 ​\text{sim}(z, z_j) 视为常数，以避免模型无论输入样本如何都会输出恒定结果的平凡解。


2.4 训练目标函数

结合公式 (5) 和公式 (6)，我们定义最终的目标函数为：

\mathcal{L} = \mathcal{L}_{tsd} + \lambda \mathcal{L}_{mslc}, \tag{7}

其中 ​\lambda 是平衡不同损失函数的权衡参数。在本文的实现中，使用余弦相似度作为相似性度量。具体而言，我们定义 ​\text{sim}(x, y) = x^\top y / \|x\| \|y\|。

在测试阶段，自适应以在线方式进行。具体来说，当在时间点 ​T 接收到图像 ​x_T 时，模型的状态会通过从上一张图像 ​x_{T-1} 更新的参数进行初始化。模型在接受新样本 ​x_T 后生成预测 ​p_T = g(x_T)，并使用公式 (7) 进行仅一步梯度下降更新模型。需要注意的是，只要存在测试数据，自适应过程可以持续进行。


TTA 论文笔记