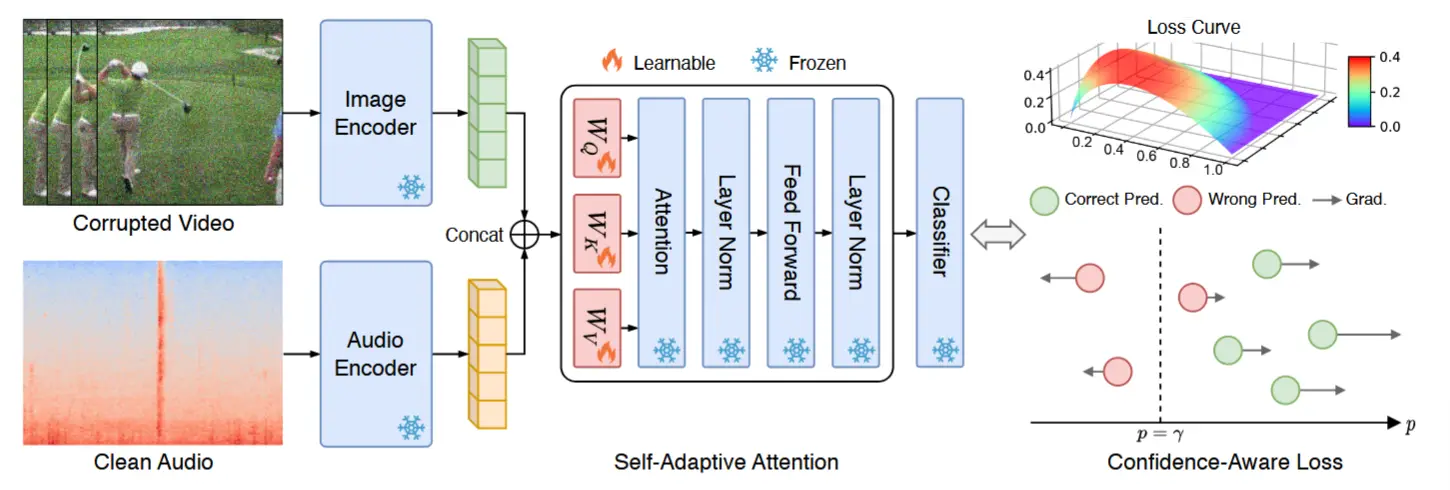
论文 - 《SMOOTHING THE SHIFT: TOWARDS STABLE TEST-TIME ADAPTATION UNDER COMPLEX MULTIMODAL NOISES》
代码 - Github
关键词 - 多模态、Test-Time Adaptation、音频、视频、ICLR2025

摘要

问题背景
- 多模态背景下的测试时自适应 (Test-Time Adaptation, TTA) 比单模态更复杂，例如多模态同时遭受损坏以及模态缺失等问题，并且来自不同分布偏移的损坏通常混合在一起。
- 现有的 TTA 方法在多模态常见下往往失败，因为剧烈的分布偏移会破坏源模型中的先验知识。
本文工作
- 本文揭示了一个新的挑战，称为 多模态野性TTA （Multimodal Wild TTA）。
- 提出了两种新颖的策略：
  - 1）基于四分位距平滑的样本识别与单模态辅助
  - 2）互信息共享 (Mutual information sharing, SuMi)
    - SuMi通过四分位距平滑化自适应过程，避免了剧烈的分布偏移。
    - 随后，SuMi充分利用单模态特征来选择低熵且包含丰富多模态信息的样本进行优化。
    - 此外，引入了互信息共享机制，用于对齐信息、减少模态间的差异并增强跨模态的信息利用率。
实验结果
- 在两个公开数据集上的大量实验表明，SuMi在多模态数据的复杂噪声模式下相较于现有方法具有显著的有效性和优越性。

1 引言

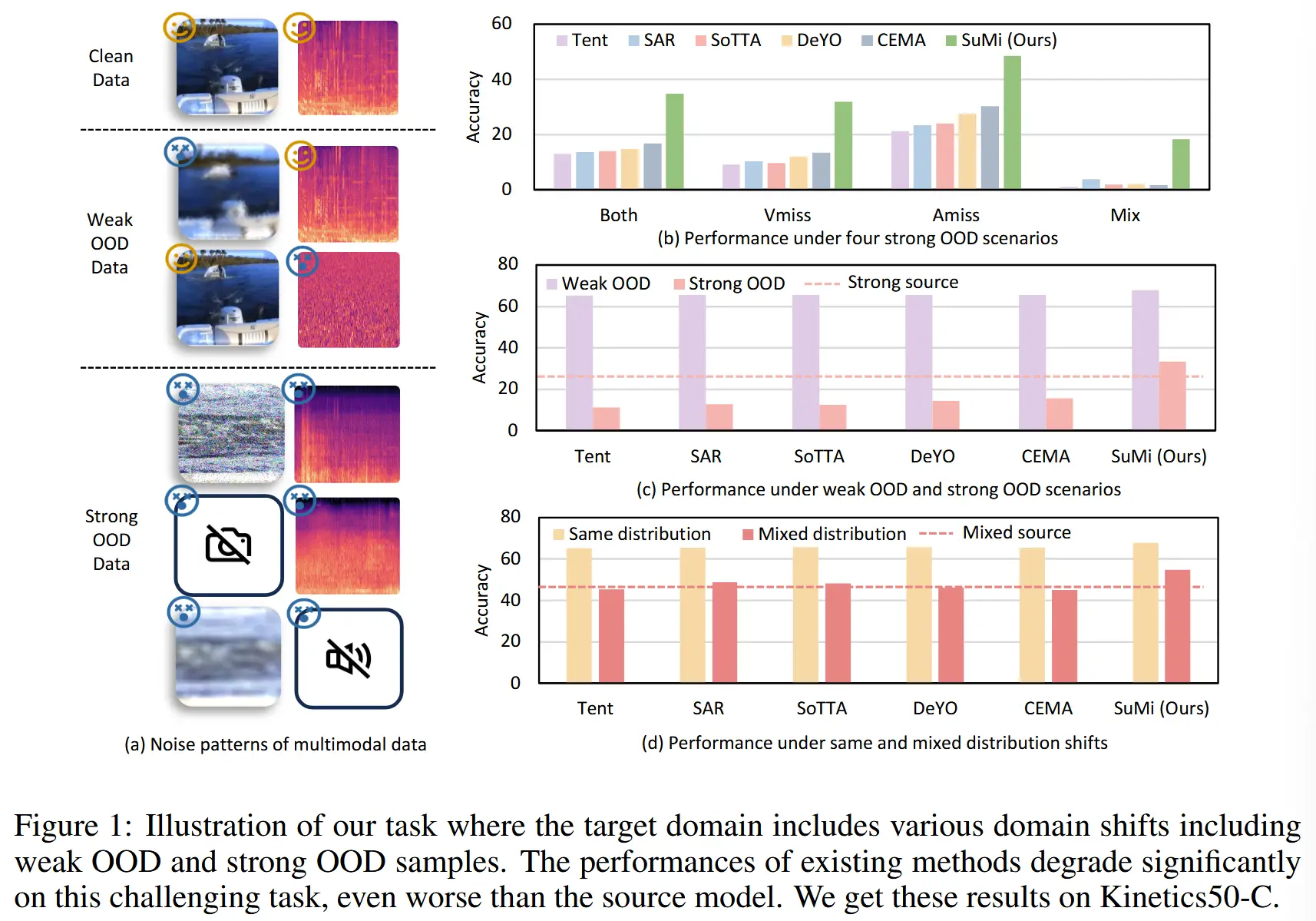
本文将多模态噪声场景大致分为两类，如图 1
- 弱分布外 weak OOD：只有一个模态受到噪声损坏。
- 强分布外 strong OOD：多个模态受到噪声损坏或出现模态缺失问题。
- 如图1(b)和(c)所示，现有TTA方法在面对多模态场景中更复杂的噪声模式时性能会显著下降，尤其是在强OOD样本的情况下。
- 如图1(d)所示，在目标域包含多种分布偏移的多模态野性TTA背景下，结果仍然不令人满意。

wild TTA ：在目标域包含多种类型分布偏移的现实动态环境。

最近较类似的工作 - READ （Yang等，2024）
- 该工作探讨了测试时多模态数据中的可靠性偏差，其提出当其中一个模态受到损坏时，模态间的可靠性平衡将被破坏，这会导致模型性能的严重下降。
- 然而，它仅讨论了弱OOD情况，忽略了多模态数据中更复杂的噪声模式。此外，它是基于测试样本具有相同分布偏移类型的温和TTA设置。

本文工作
- 揭示了 多模态野性TTA 的挑战，其中目标域包含多种类型的分布偏移，包括弱OOD样本和强OOD样本。
- 为了避免剧烈的分布偏移破坏源模型中的先验知识，我们提出通过 四分位距平滑化自适应过程。
- 此外，我们充分利用单模态信息来选择低熵且富含多模态信息的样本。
- 最后，我们提出互信息共享以对齐不同模态之间的信息，这可以减少不同模态之间的差异并增强不同模态的信息利用率。

2 相关工作

测试时训练 (Test-Time Training, TTT)
- 定义：在训练阶段通过监督和自监督目标训练源模型，以增强测试时自适应能力。
- 局限：这些方法依赖于代理任务，并假设训练过程是可控的，这限制了其应用范围。
- 例子：TTT（Sun等，2020）和TTT+（Liu等，2021）。
完全测试时自适应 (Fully Test-Time Adaptation, FTTA)
- 定义：仅在测试阶段对模型进行自适应调整，而无需干预训练阶段。
- 例子：Tent（使用熵最小化来更新模型的归一化层）、SAR & EATA（提出了用于熵最小化的样本选择标准）、DeYO（结合熵和新提出的PLPD指标来识别样本）、CEMA（一种动态不可靠和低信息量样本排除方法以实现熵最小化）。
多模态 TTA
- Shin等（2022）提出了一种框架，用于生成跨模态伪标签作为自训练信号。
- Guo等（2024b）提出了一种多模态TTA方法，但专注于多模态回归任务。
- Yang等（2024）探索了多模态TTA，并提出了可靠融合和鲁棒自适应方法以解决多模态数据中的信息差异问题。即前面提到的 READ 方法。

3 方法论

3.1 问题定义

以两种模态为例进行问题定义。

（源模型定义）设源模型 M_\theta = (\phi_{u_1}, \phi_{u_2}, F) ，其参数为 \theta ，基于源域数据集 D_{\text{source}} = {(x_i, y_i)}_{i=1}^{N_s} 预训练，其中 \phi_{u_1} 和 \phi_{u_2} 分别是模态 u_1 和 u_2 的编码器，F 是带有预测头的多模态融合层，样本输入 x_i = (x_{u_1}^i, x_{u_2}^i) ，且 N_s 是样本数量。

（TTA 定义） TTA 旨在无需标签和源数据集的情况下，在目标域数据集 D_{\text{target}} = \{x_i\}_{i=1}^{N_t} 上对源模型 M_\theta 进行微调。现有TTA方法（Niu等，2023；Yang等，2024）通过最小化测试域数据的熵来更新参数 \theta ：

\text{Ent}_\theta(x) = -\mathbf{p}_\theta(x) \log \mathbf{p}_\theta(x) = -\sum_{i=1}^{C} p_\theta(x)_i \log p_\theta(x)_i \tag{1}

其中，p_\theta = \text{softmax}(M_\theta(x)) = (p_\theta(x)_1, p_\theta(x)_2, \cdots, p_\theta(x)_C) 是模型 M_\theta 输出的概率分布，C 是类别数量。

SuMi的整体架构如图2所示。

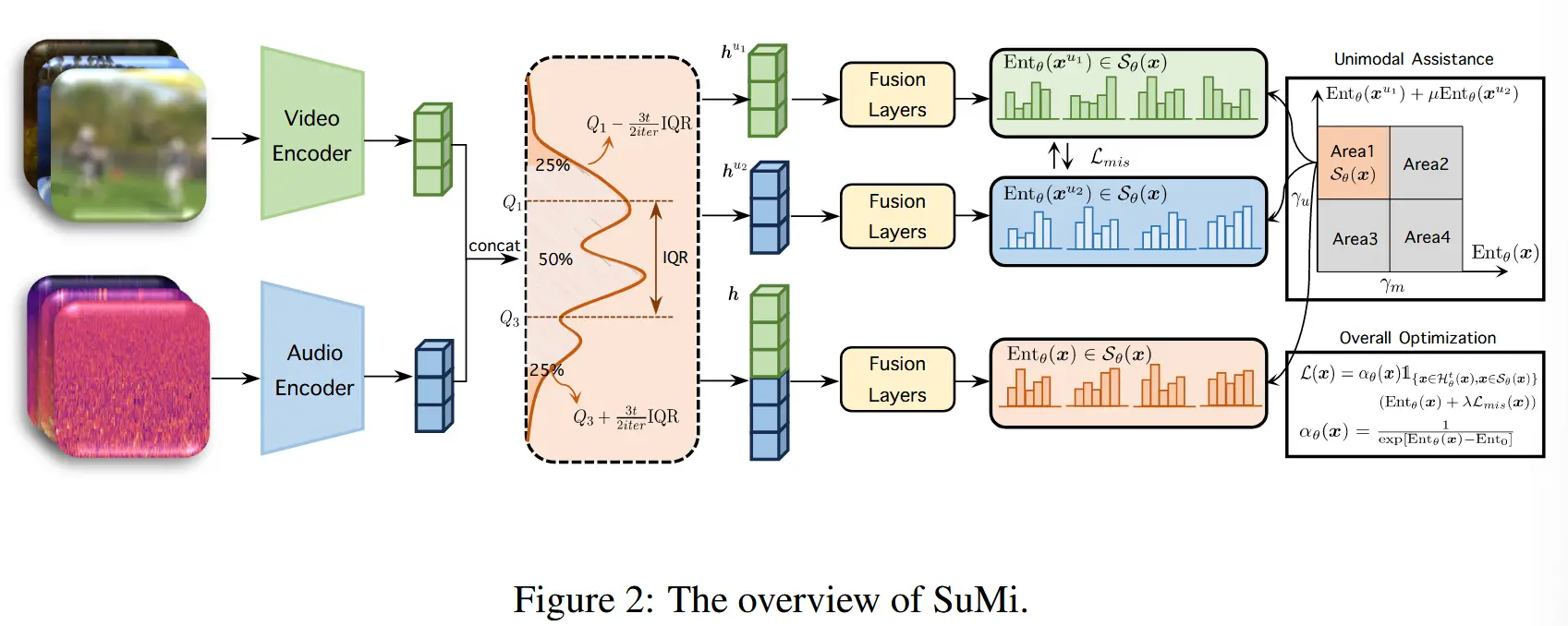
3.2 基于四分位距平滑与单模态辅助的样本识别

3.2.1 四分位距平滑

四分位距平滑（INTERQUARTILE RANGE SMOOTHING）

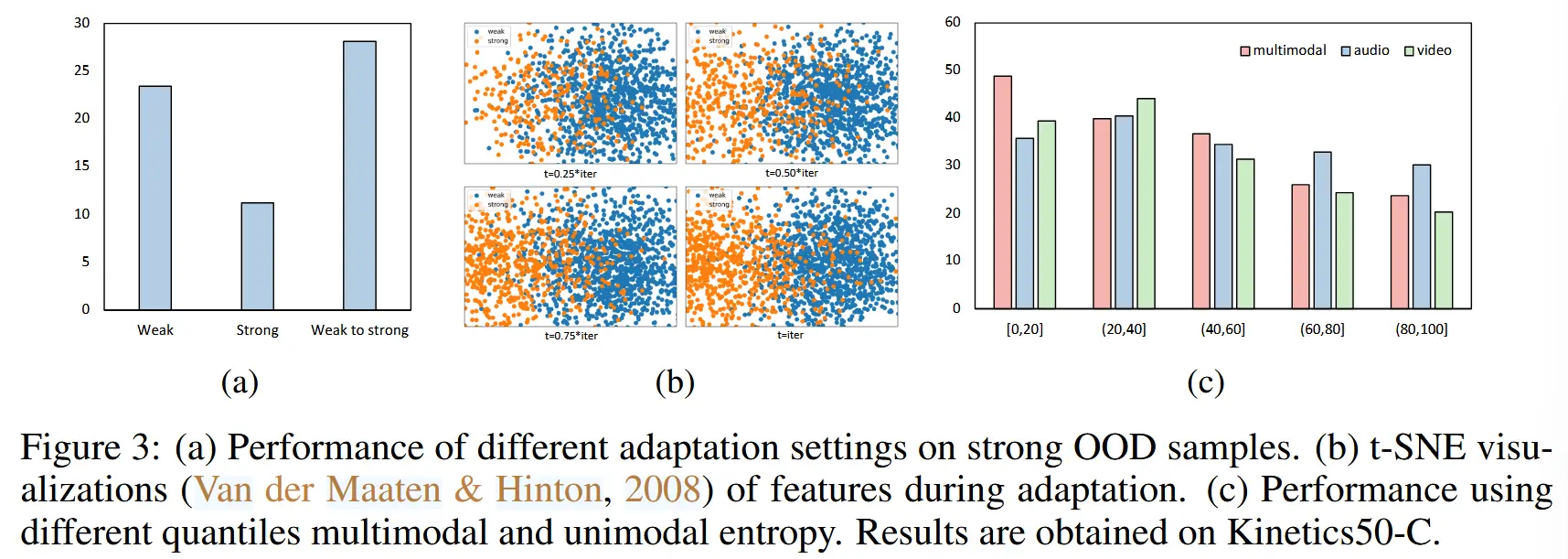
（灵感来源） 在图3(a)中，展示了三种不同自适应过程设置的性能表现。可以看到，直接适配强OOD性能会很差，而先从弱OOD再到强OOD性能有所提升。主要原因在于源域与强OOD域之间分布差距较大，直接适配会破坏源模型的先验知识，并导致不稳定性。-->平滑的适配过程远优于剧烈的适配过程

（四分位距平滑方法） 用于在适配过程中动态识别样本。四分位距（IQR）是一种统计离散度的度量，表示数据的分布范围。以下是对IQR的简要定义：

（IQR定义） 四分位距（IQR）是数据的第75%与第25%之间的差值。通过线性插值将数据分为四个有序的部分，分别表示为 Q_1 （下四分位数）、 Q_2 （中位数）和 Q_3 （上四分位数）。IQR 的计算公式为：\text{IQR} = Q_3 - Q_1

IQR 常用于识别数据集中的不稳定样本或异常值。具体而言，根据 Tukey 的规则（Tukey 等，1977），稳定的样本集合 \mathcal{X}_s 被选择为：

\mathcal{X}_s = \left\{ x \mid x \geq Q_1 - \frac{3}{2} \text{IQR} \quad \text{and} \quad x \leq Q_3 + \frac{3}{2} \text{IQR} \right\} \tag{2}

（IQR样本选择） 为了平滑适配过程，我们对上述公式稍作修改，并选择样本集合 \mathcal{H}_\theta^t(x) 为：

\mathcal{H}_\theta^t(x) = \left\{ h \mid h \geq Q_1 - \frac{3}{2} f(t) \text{IQR} \quad \text{and} \quad h \leq Q_3 + \frac{3}{2} f(t) \text{IQR} \right\} \tag{3}

h = [h^{u_1}, h^{u_2}], \, h^{u_1} = \phi_{u_1}(x^{u_1}), \, h^{u_2} = \phi_{u_2}(x^{u_2}) \tag{4}

其中， t 是当前迭代次数，\theta 是模型的参数，f(t) 是平滑函数，[,] 表示拼接操作，而 h 是样本的表示。为了简化，我们使用线性平滑，并设置 f(t) = t / \text{iter} ，其中 \text{iter} 是总迭代次数。我们使用表示（representations）而非原始输入，因为表示是包含较少噪声和无关信息的、更具信息量的密集向量，相较于原始输入更为纯净。在第 t 次迭代时，我们使用所选数据 \mathcal{H}_\theta^t(x) 进行适配。

如图3(b)所示，我们通过源模型可视化了样本识别过程。从图中可以看出，在最初的几次迭代中，大多数弱OOD样本被选中。随着 t 的增加，用于适配的数据也在不断增加，逐渐包括越来越多的强OOD样本。这种平滑过程能够实现对强OOD样本和各种类型分布偏移的渐进式适配，从而避免剧烈的分布差距破坏源模型的先验知识。此外， h 是一个向量。因此，在实际操作中，如果向量 h 中有 \beta + (1 - \beta)f(t) 的值满足公式(3)，则将其选为适配对象，以确保稳定性。

3.2.2 单模态辅助

（当前局限） 四分位距平滑旨在帮助模型 保留源模型中的先验知识，并 逐步适配到强OOD样本和各种类型的分布偏移。然而，这一过程 无法区分对熵最小化有益的高质量样本。

（解决办法） 引入了一种针对多模态数据的新颖样本识别方法。已知 低熵样本有助于熵最小化，而高熵样本由于其不确定性会对其产生不利影响。然而，在多模态数据的背景下，除了多模态熵之外，我们还可以利用单模态熵来辅助适配。

（实验分析） 如图3(c)所示，作者在实验中使用了单模态熵和多模态熵。可以得到以下结论：

多模态：低熵样本的表现明显优于高熵样本。
单模态：无论是音频还是视频，区间为 ((20, 40]) 的样本比区间为 ([0, 20]) 的样本表现更好。

（实验原因分析） 当仅有一个模态表现出低熵时，这表明该样本不依赖于多模态数据进行准确预测，意味着它对多模态优化的贡献较低。相反，一个稍微高一点熵的单模态样本显示出对多模态数据的依赖性，表明它包含丰富的多模态信息。

该结果原因可以理解为，当仅单模态低熵时，不需要另一个模态的熵既可以得到确定性输出，即该样本不依赖另一个模态，或者说该样本对于本文的多模态任务不重要。而单模态熵在区间 [20,40] 的样本，既保留了低熵有助于熵最小化的优势（高确定性），同时保证了该样本对于多模态的依赖（高信息量）。

（提出方法设计） 受上述观察的启发，我们提出了一种基于单模态辅助的样本识别方法，用于选择具有丰富多模态信息的低熵样本。具体而言，我们的方法采用以下识别标准：

\mathcal{S}_\theta(x) = \left\{ x \mid \text{Ent}_\theta(x) \leq \gamma_m \quad \text{and} \quad (\text{Ent}_\theta(x^{u_1}) + \mu \text{Ent}_\theta(x^{u_2})) \geq \gamma_u \right\} \tag{4}

其中，\gamma_m 和 \gamma_u 分别是预定义的多模态熵和单模态熵阈值， \mu 是模态之间的权衡因子。通过 限制多模态熵，我们可以选择具有高确定性和较少噪声的低熵样本。同时，通过 限制单模态熵，我们可以确保所选样本包含丰富的多模态信息，排除低信息量的样本。

3.3 互信息共享

（可靠性偏差） Yang等提出，这指的是不同模态之间的信息差异。在适配过程中，这种差异往往会导致各模态的利用不均衡。

（进一步扩展） 在强OOD情况下，可能会出现模态缺失或多模态同时受损的情况，从而进一步加剧这种不平衡现象。因此，如何平衡不同模态的适配过程变得尤为重要。

（解决） 作者提出了一种简单而有效的方法—— 互信息共享，以对齐不同模态之间的信息。具体而言，对于模态 u_i，我们可以通过以下方式获得其概率分布：

p^{u_i}_\theta(x^{u_i}) = \text{softmax}(F(\phi_{u_i}(x^{u_i})))

为了简化表示，我们将 \mathbf{p}_{\theta}^{u_i}(x^{u_i}) 简记为 \mathbf{p}^{u_i} 。我们定义 \mathbf{p}^{u_i} 的 互补概率分布 为：

\mathbf{p}^{u_i'} = \frac{\sum_{j=1}^M \mathbf{p}^{u_j} - \mathbf{p}^{u_i}}{(M-1)} \tag{5}

其中， M 是模态的数量。对于两个模态的情况， \mathbf{p}^{u_1'} = \mathbf{p}^{u_2} 且 \mathbf{p}^{u_2'} = \mathbf{p}^{u_1} 。为了 改善不同模态之间的对齐，我们可以最小化概率分布 \mathbf{p}^{u_i} 和其互补分布 \mathbf{p}^{u_i'} 之间的 KL散度。

（新问题） 然而，如果某一模态严重受损，最小化KL散度可能会 对干净的模态产生影响。因此，我们引入多模态分布 \mathbf{p}^m = \text{softmax}(M_\theta(x)) ，以提高鲁棒性和稳定性。因此，我们可以将互信息共享损失表示为：

\mathcal{L}_{mis}(x) = D_{KL}(\mathbf{p}^{u_1} \parallel \frac{1}{2} (\mathbf{p}^{u_1'} + \mathbf{p}^m)) + D_{KL}(\mathbf{p}^{u_2} \parallel \frac{1}{2} (\mathbf{p}^{u_2'} + \mathbf{p}^m)) \\ = \sum_{i=1}^C p_i^{u_1} \log \frac{2 p_i^{u_1}}{p_i^{u_1'} + p_i^m} + \sum_{i=1}^C p_i^{u_2} \log \frac{2 p_i^{u_2}}{p_i^{u_2'} + p_i^m} \tag{6}

注意：原本是单模态概率分布与互补分布的KL散度，由于担心某模态严重受损影响另一个干净模态，引入多模态概率分布来中和，KL散度的另一边使用了 \frac{1}{2} (\mathbf{p}^{u_1'} + \mathbf{p}^m) 。

其中， C 是类别数量， p_i 是向量 \mathbf{p} 的第 i 个值。互信息共享可以帮助模型连接和对齐不同模态之间的信息。通过互信息共享，当存在受损模态（包括模态缺失）时，其他模态的信息可以被利用来增强预测结果。

3.4 总体优化

（为样本设计权重） 沿袭先前的TTA方法，在适配过程中添加了一个加权项以强调样本的贡献。具体而言，加权项的计算公式为：

\alpha_\theta(x) = \frac{1}{\exp[\text{Ent}_\theta(x) - \text{Ent}_0]} \tag{7}

其中， \text{Ent}_0 是预定义的归一化因子。综上所述，我们可以将总体损失函数表示为：

\mathcal{L}(x) = \alpha_\theta(x) \mathbf{1}_{\{x \in \mathcal{H}_\theta^t(x), x \in \mathcal{S}_\theta(x)\}} (\text{Ent}_\theta(x) + \lambda \mathcal{L}_{mis}(x)) \tag{8}

其中， \mathbf{1}_{\{\cdot\}}(\cdot) 是指示函数，\lambda 是两项损失之间的权衡参数。

对于强OOD适配，仅在适配过程的前 t_0 次迭代中添加互信息共享损失 \mathcal{L}_{mis}。 原因在于，随着迭代次数的增加，IQR平滑会包含越来越多的强OOD样本，而这些样本中多个模态可能受到损坏，这可能会破坏信息共享并对模型性能造成损害。对于弱OOD适配，我们在所有迭代中均添加互信息共享损失。

总体而言，算法1展示了我们方法的总体框架。

4 实验

4.1 实验设置

数据集
- Kinetics50-C、VGGSound-C
- 视频15种损坏，音频6种损坏，5个严重程度
- 对于strong OOD，引入四种类型：Both （两个模态均受损）、Vmiss （视频模态缺失）、Amiss （音频模态缺失）、Mix （一个模态缺失，另一个模态受损）。
实验细节
- 模型：CAV-MAE
- 优化器Adam
- 参数设置略
- 更新归一化层的仿射参数

4.2 sota对比

对比方法：Tent, EATA, SAR, SoTTA, CEMA, DeYO, READ

4.2.1 单域

这里的“域”即 偏离域 = 损坏程度

表1：Kinetics50-C上对视频模态（5级损坏）

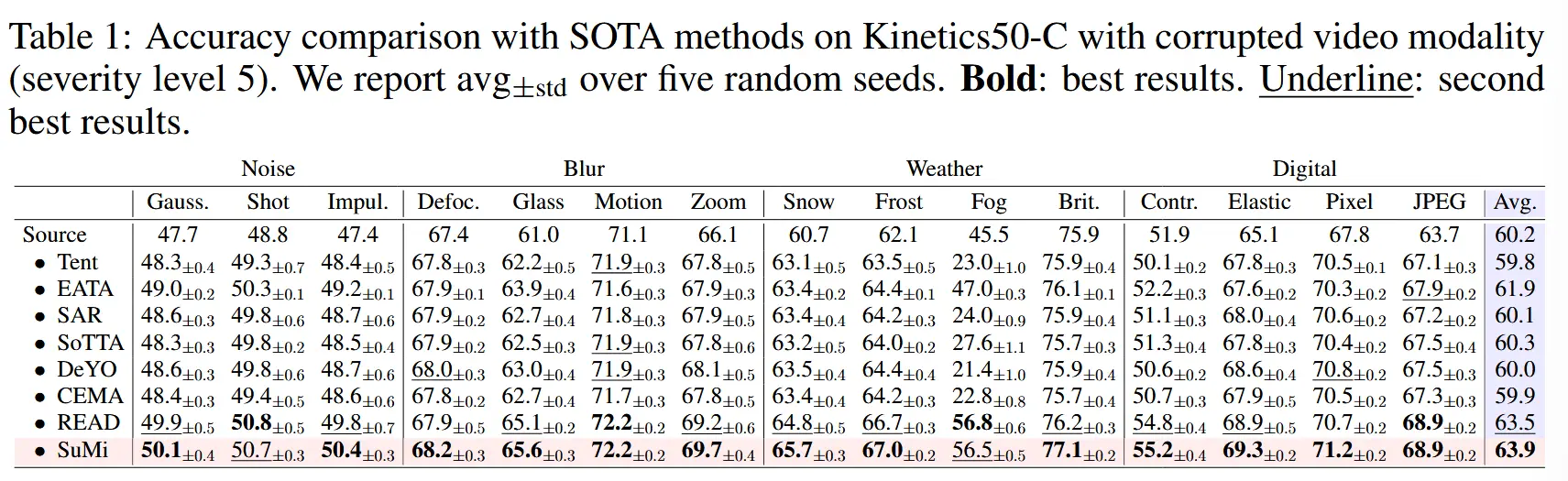
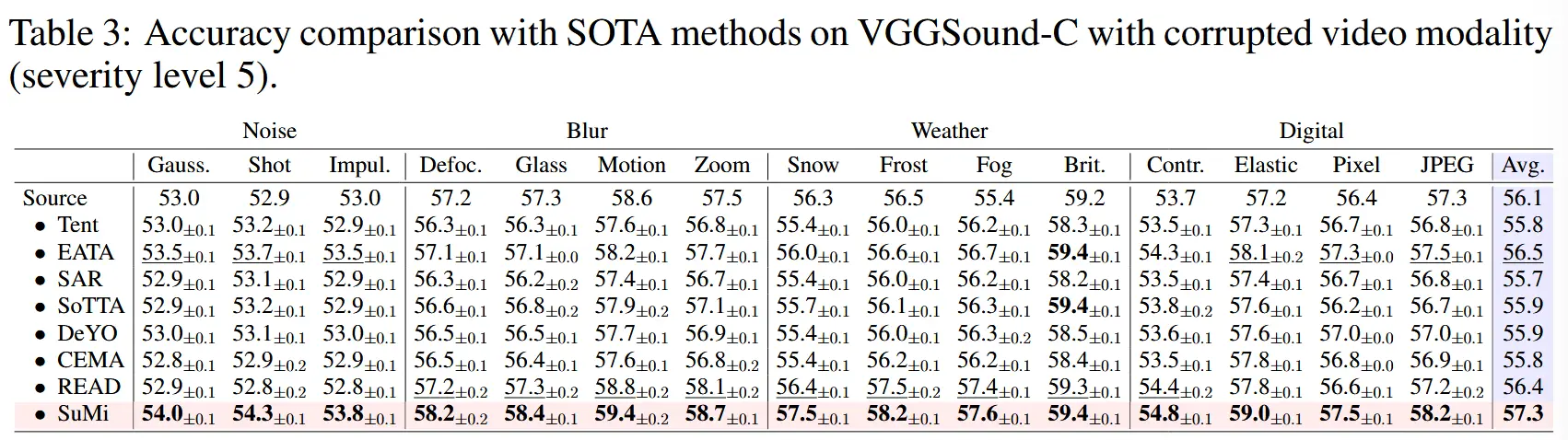
表3：VGGSound-C上对视频模态（5级损坏）

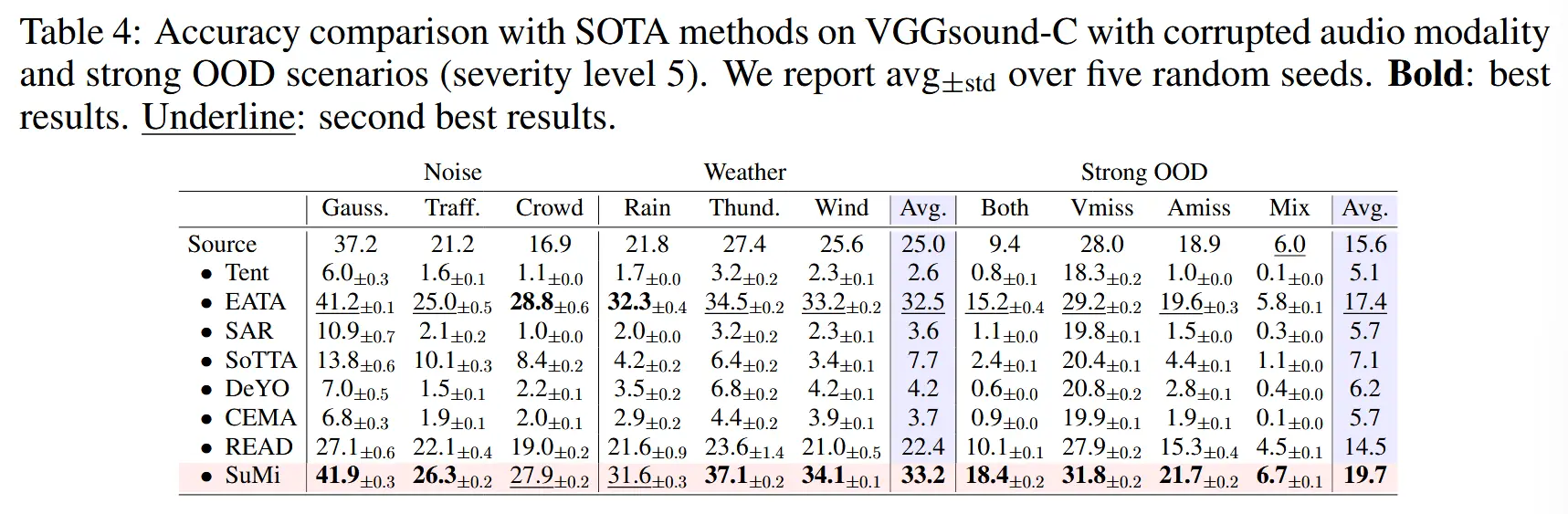
表2：Kinetics50-C上音频模态和strongOOD场景（5级损坏）
- 对于4种强OOD损坏类型，大多数现有SOTA方法的表现甚至不如源模型。 EATA和READ表现较好，但是在Mix场景下也大幅下降，不如源模型。
- SuMi在所有四种分布场景中均显著优于其他方法。

表4：VGGSound-C上音频模态和strongOOD场景（5级损坏）
- 分析同表2

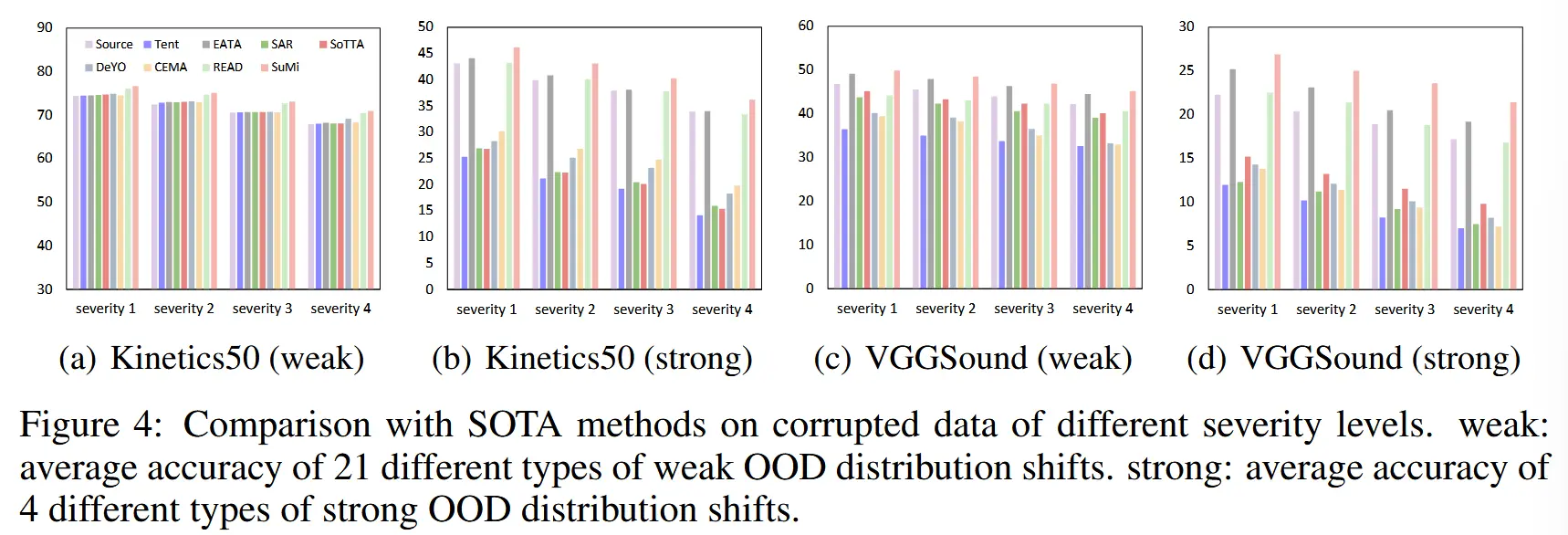
图4：对不同严重性级别的损坏数据进行比较
- weak：21 种不同类型的弱 OOD 分布偏移的平均准确性。
- strong：4 种不同类型的强 OOD 分布偏移的平均准确性。
- 大多数方法在弱OOD样本上表现良好，但在强OOD样本上失败。

4.2.2 混合域

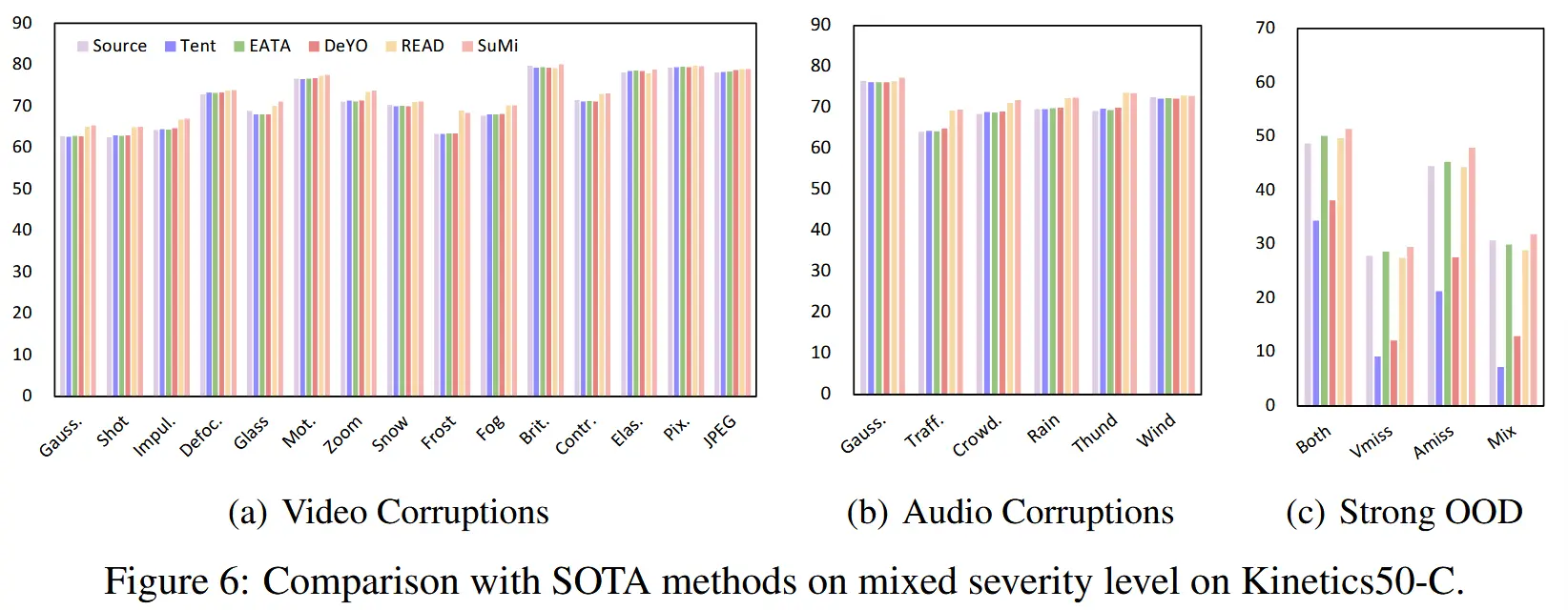
图5：10 种不同比例的强 OOD 样品的混合损坏数据进行比较。
- (a)和(b)显示了严重程度为5的结果：当强OOD样本比例较低时，所有方法表现良好；但随着比例增加，大多数方法性能迅速下降，甚至不如源模型。原因是源域与强OOD域之间的巨大分布差距破坏了源模型的先验知识。
- (c)和(d)增加了混合严重程度的场景，结论相同。

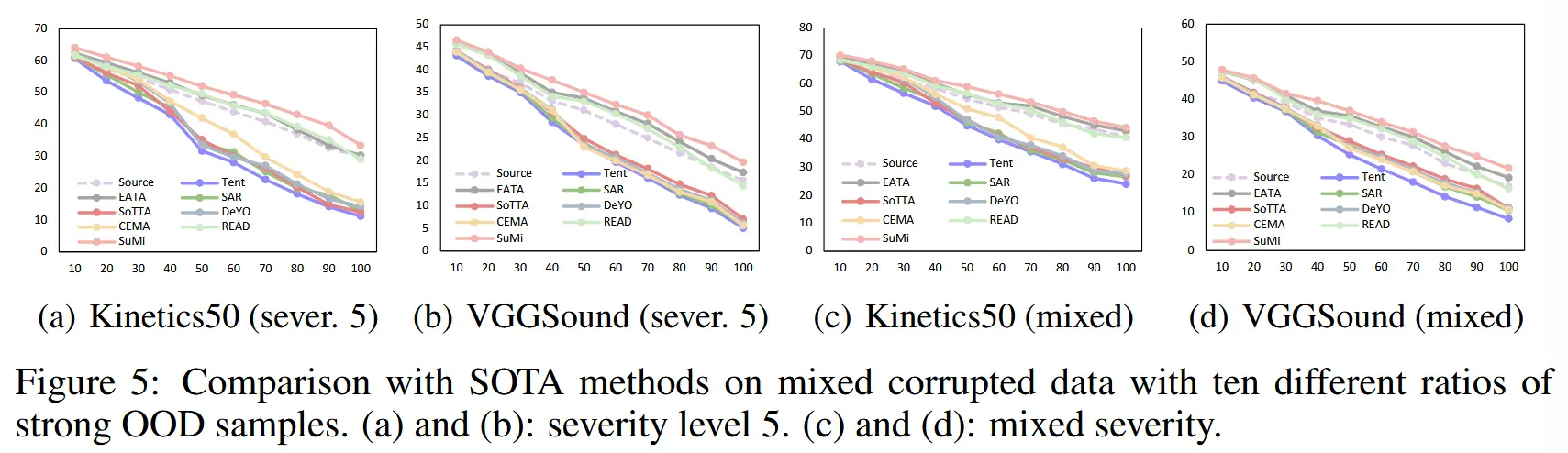
图6：Kinetics50-C 上严重性级别混合
- 在混合严重程度下，SuMi仍能在大多数分布偏移中取得一致的改进，优于其他SOTA方法。

4.3 消融

各组件贡献
- IQR平滑化 对模型性能提升最大，因为它能够弥合源域与强OOD域之间的差距.

单模态辅助的探索
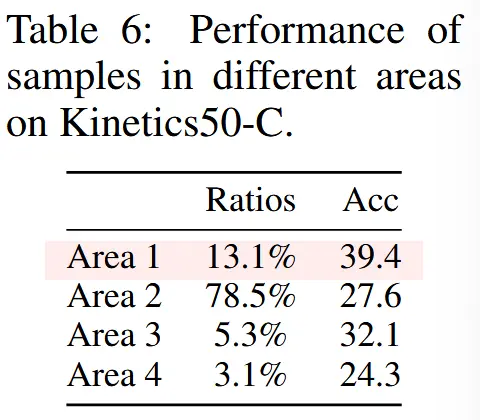
- 在公式(4)和图2中，样本被分为四个区域，分别是高/低熵 + 高/低多模态信息的两两组合。
- 表6展示了这四个区域在Kinetics50-C上的性能表现。

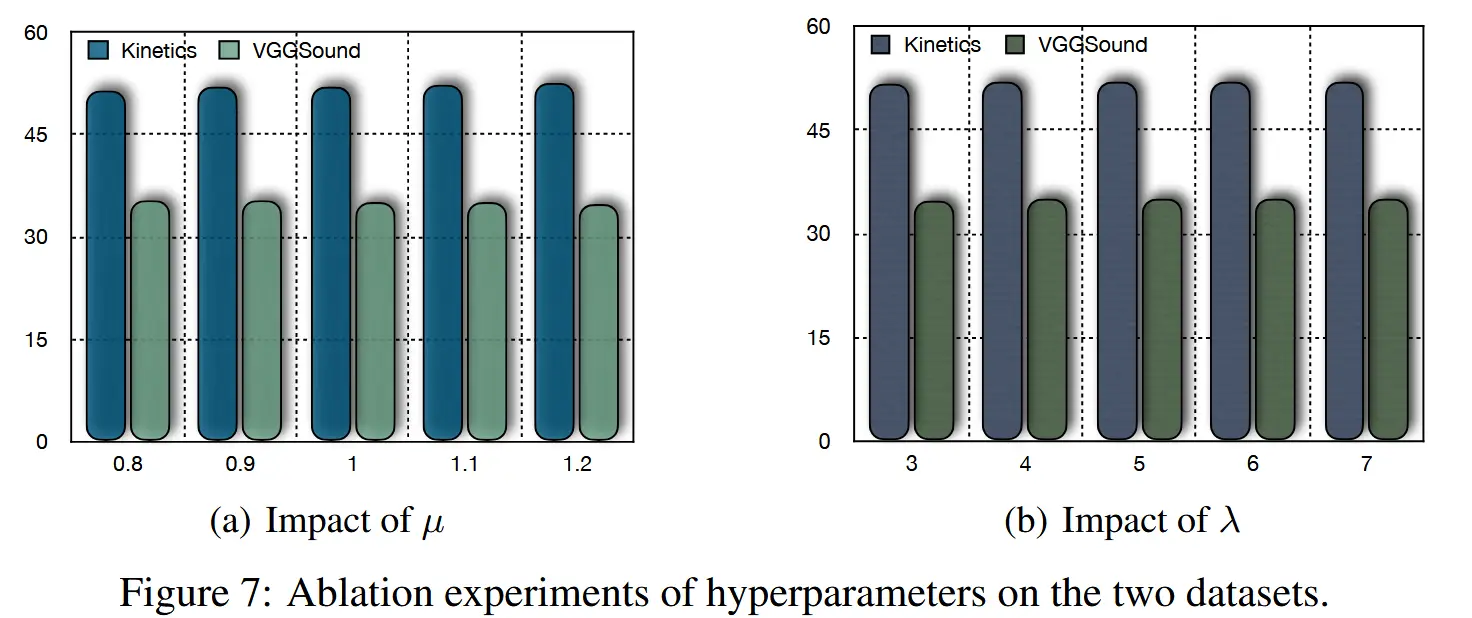
超参数探索
- 权衡系数 \mu
  - 图7(a)探索了公式(4)中的权衡系数 \mu 对两个数据集的影响，
  - 随着 \mu 增加，Kinetics50-C（视频主导的数据集）性能提升，而VGGSound-C（音频主导的数据集）性能下降。
  - 这是因为为占主导地位的模态增加权重会降低性能，而单模态辅助的目标是选择富含多模态信息的样本。
- 权重项 \lambda
  - 增加权重项 \lambda 可以略微提升性能。
  - 互信息共享在不同 \lambda 值下表现出稳定性。

5 总结

在本文中，我们提出了一项新的实用且具有挑战性的任务，称为多模态野生 TTA。为了解决这个问题，我们提出了使用四分位间距平滑和单峰辅助以及互信息共享（SuMi）进行样本识别。SuMi 通过使用四分位距平滑适应，弥合了源域和强 OOD 域之间的差距。此外，SuMi 利用单峰特征选择具有丰富多模态信息的低熵样本进行优化。最后，提出了相互信息共享，以进一步调整信息并减少不同模式之间的差异。我们在两个广泛使用的多模态数据集上进行了广泛的实验，其中 SuMi 的性能显着且一致地优于现有的 TTA 方法，表明了它的有效性。然后进行消融实验以验证每个成分的贡献。

论文笔记《Smoothing the Shift: Towards Stable Test-Time Adaptation under Complex Multimodal Noises》

摘要