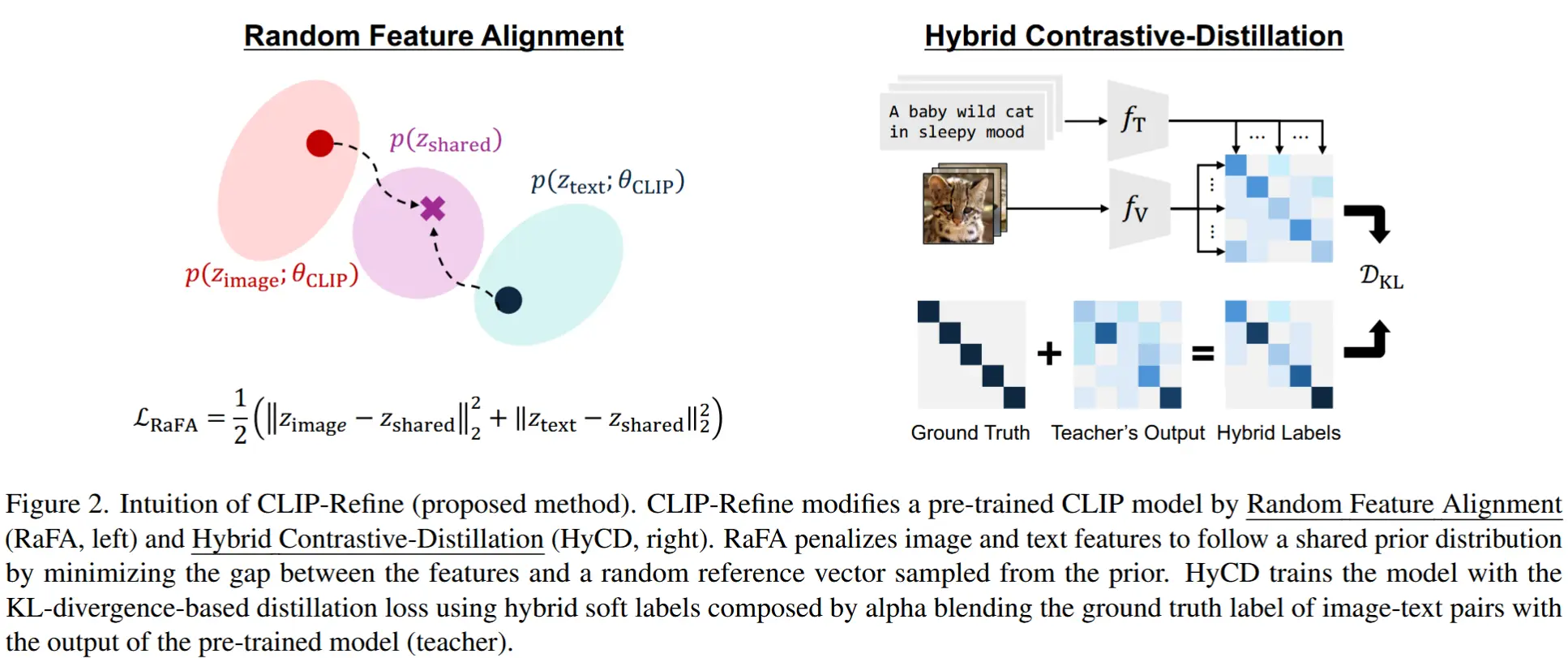
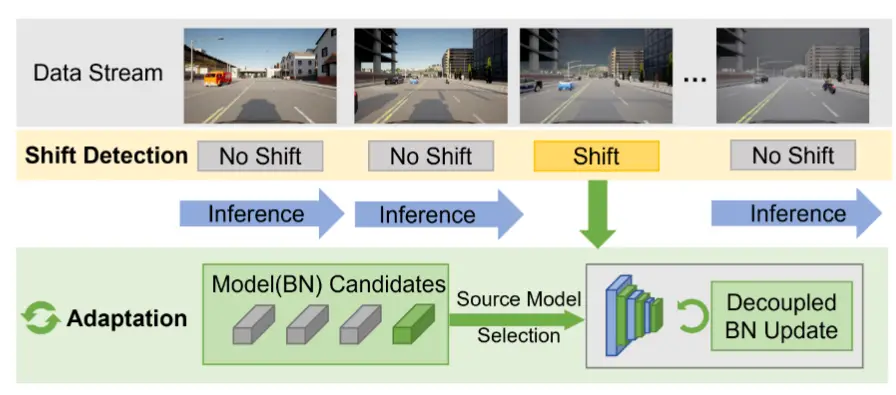
- 论文 - 《Improving Test-Time Adaptation via Shift-agnostic Weight Regularization and Nearest Source Prototypes》
- 关键词 - TTA、权重正则化、伪原型、熵、warm-up、ECCV2022
摘要
- 研究问题:TTA,在测试时自适应过程中,如果使用未标注的在线数据对整个模型参数进行更新,可能会因为无监督目标带来的错误信号而对模型产生负面影响。
- 本文工作
- 提出了一种与分布偏移无关的权重正则化方法(shift-agnostic weight regularization) ,该方法在测试时自适应过程中鼓励对那些对分布偏移敏感的模型参数进行较大更新 ,而对那些不敏感的参数进行较小更新 。这种正则化机制使得模型能够在利用较大学习率带来优势的同时,快速适应目标域,且不会造成性能下降。
- 设计了一个基于最近源原型(nearest source prototypes)的辅助任务 ,用于对齐源域和目标域的特征表示。该任务有助于减小源域与目标域之间的分布差异,从而进一步提升模型性能。
1 引言
- 本文提出了两种全新的测试时自适应方法
- (1)与分布偏移无关的权重正则化(Shift-Agnostic Weight Regularization, SWR),该方法使得模型能够快速地适应目标域,尤其在使用较大学习率对整个模型参数进行更新时具有显著优势。从分布偏移的角度来看,SWR 将模型的所有参数划分为两类:对分布偏移不敏感的参数 和 对分布偏移敏感的参数 ,并对前者进行较小幅度的更新、对后者进行较大更新。
- (2)无参数最近源原型分类器(Nearest Source Prototype, NSP) 的辅助任务,该任务将目标域样本的特征表示拉近其对应的最近源域原型。通过 NSP 分类器,源域和目标域的特征表示可以得到良好的对齐,从而显著提升主任务的性能。
方法需要在模型部署前访问源域数据,用于识别 shift-agnostic 与 shift-biased 参数,并生成源原型。但是并未改变模型的预训练方式。
2 方法介绍
假设在源域上训练的模型参数 \theta 包含编码器部分 \theta_e 和分类器部分 \theta_c。TTA过程中,本文方法的总损失定义为:
其中:
- w_l 表示惩罚向量 \boldsymbol{w} 的第 l 个元素,用于控制模型参数的更新;
- \theta_l 是模型第 l 层的参数向量,\theta_l^* 是前一步更新的参数;
- \lambda_r 是正则化项的重要性系数;
- \mathcal{L}_{\theta_e, \theta_c}^{\text{main}} 和 \mathcal{L}_{\theta_e}^{\text{aux}} 分别表示主任务损失和辅助任务损失。
优化主任务损失会更新整个模型参数 \theta_e 和 \theta_c,而优化辅助任务损失仅更新编码器部分 \theta_e。
公式1就是本文方法在TTA过程中的总损失函数:第一个是主任务的损失,对应公式3;第二个是辅助任务损失,作者设计了NSP辅助任务来更新编码器;第三个是正则化项,控制模型参数更新幅度。
2.1 与分布偏移无关的权重正则化
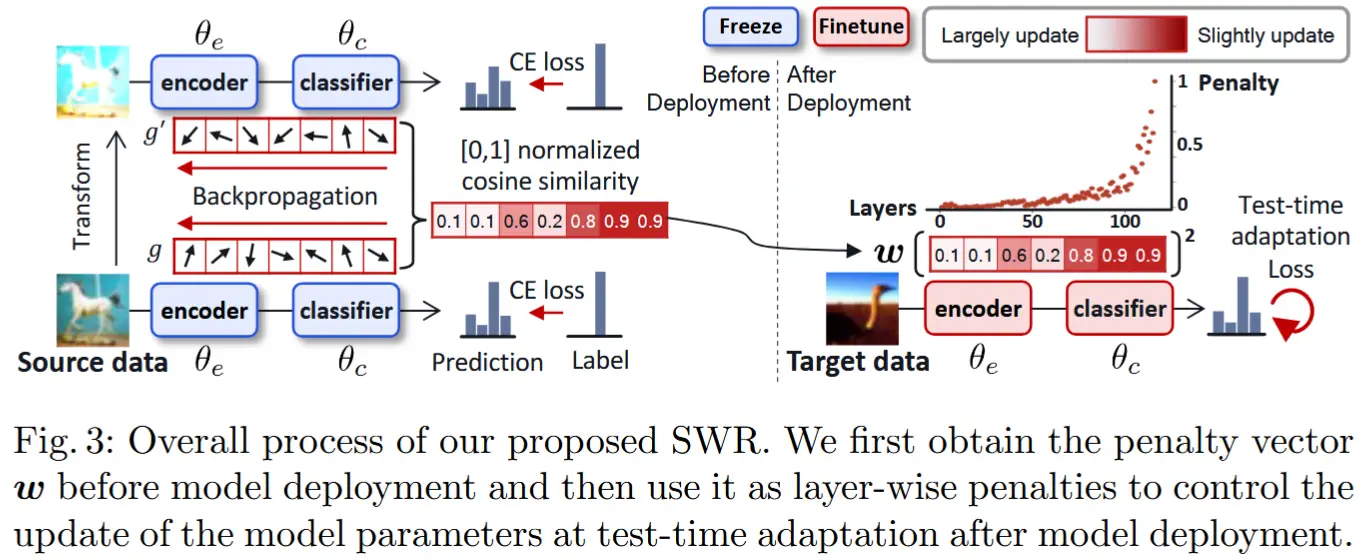
SWR 的核心思想:在TTA步骤前,通过变换技术(如颜色失真和高斯模糊)模拟分布偏移,根据梯度变化确定每个参数对分布偏移的敏感性。在TTA过程中,根据敏感性施加不同的惩罚。
获得惩罚向量 \boldsymbol{w} :首先将原始图像及其变换后的图像通过预训练的源模型进行 前向和反向传播(利用源标签交叉熵损失)。分别得到两组梯度向量 \boldsymbol{g} 和 \boldsymbol{g}',每组包含 L 个梯度向量,其中 L 是模型的总层数。然后,惩罚向量 \boldsymbol{w} 的第 l 个元素 w_l 通过计算来自 N 个源样本的两个梯度向量 \boldsymbol{g}_l^i 和 \boldsymbol{g}_l'^i 的平均余弦相似度 s_l 来计算:
其中:
- \nu[\cdot] 表示范围为 [0, 1] 的min-max normalization;
- \boldsymbol{g}_l^i 和 \boldsymbol{g}_l'^i 分别表示第 i 个源样本及其变换样本的第 l 层梯度向量;
- N 表示样本总数。
注意,惩罚向量 \boldsymbol{w} 是在模型部署前从冻结的预训练源模型中获取的,因此该过程独立于源模型的预训练方式,并且在模型部署后不需要源数据,如图 2 所示。
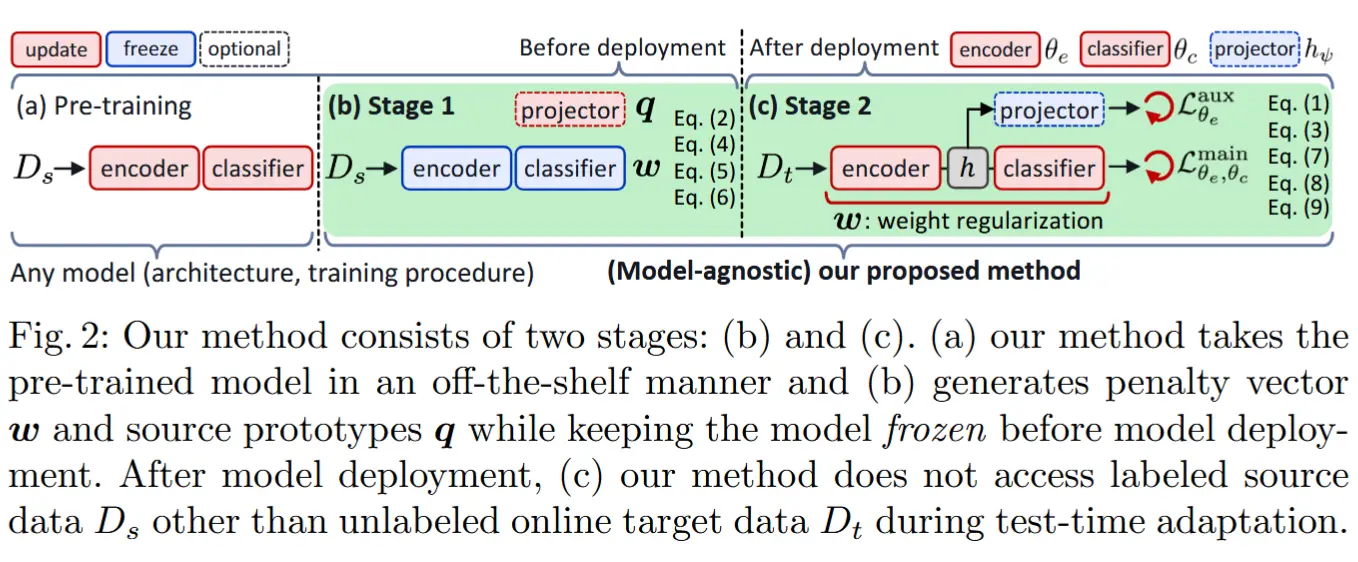
在TTA过程中,将层级惩罚值 w_l 应用于每一层的当前参数与前一步参数之间的差异。因此,属于两个梯度向量之间余弦相似度较高的层的模型参数被认为是与分布偏移无关的,通过施加高惩罚来较少更新这些参数。
2.2 主任务的熵目标
模型的主要任务 f_\theta 被定义为编码器参数 \theta_e 和分类器参数 \theta_c 执行的任务。在测试时,主任务的损失函数是基于目标分布上模型预测 \tilde{y} 的熵构建的。作者采用信息最大化损失,作为主任务的无监督学习目标。该损失由熵最小化和均值熵最大化组成,公式如下:
其中:
- H(p) = -\sum_{k=1}^C p^k \log p^k ;
- \bar{y} = \frac{1}{N} \sum_i \tilde{y}_i;
- \lambda_{m_1} 和 \lambda_{m_2} 表示每一项的重要性;
- 类别数和批量大小分别用 C 和 N 表示。
直观地讲,熵最小化使得单个预测更加自信,而均值熵最大化鼓励批量内的平均预测接近均匀分布。
TTA中非常经典的熵损失函数,将类内的特征空间聚合在一起,而类间的特征空间拉远。
2.3 基于最近源原型(NSP)的辅助任务
由于源域和目标域之间的分布偏移,在测试时目标特征会偏离源特征。为了解决这一问题,作者提出了一种基于最近源原型(Nearest Source Prototype, NSP)分类器的辅助任务,该任务将目标嵌入拉近到其在嵌入空间中的最近源原型。最终,优化辅助任务可以显著提升性能,因为它通过对齐源域和目标域的表示直接支持主任务。
源原型生成
注意源原型的生成是TTA前的步骤,并使用源域样本训练投影层。
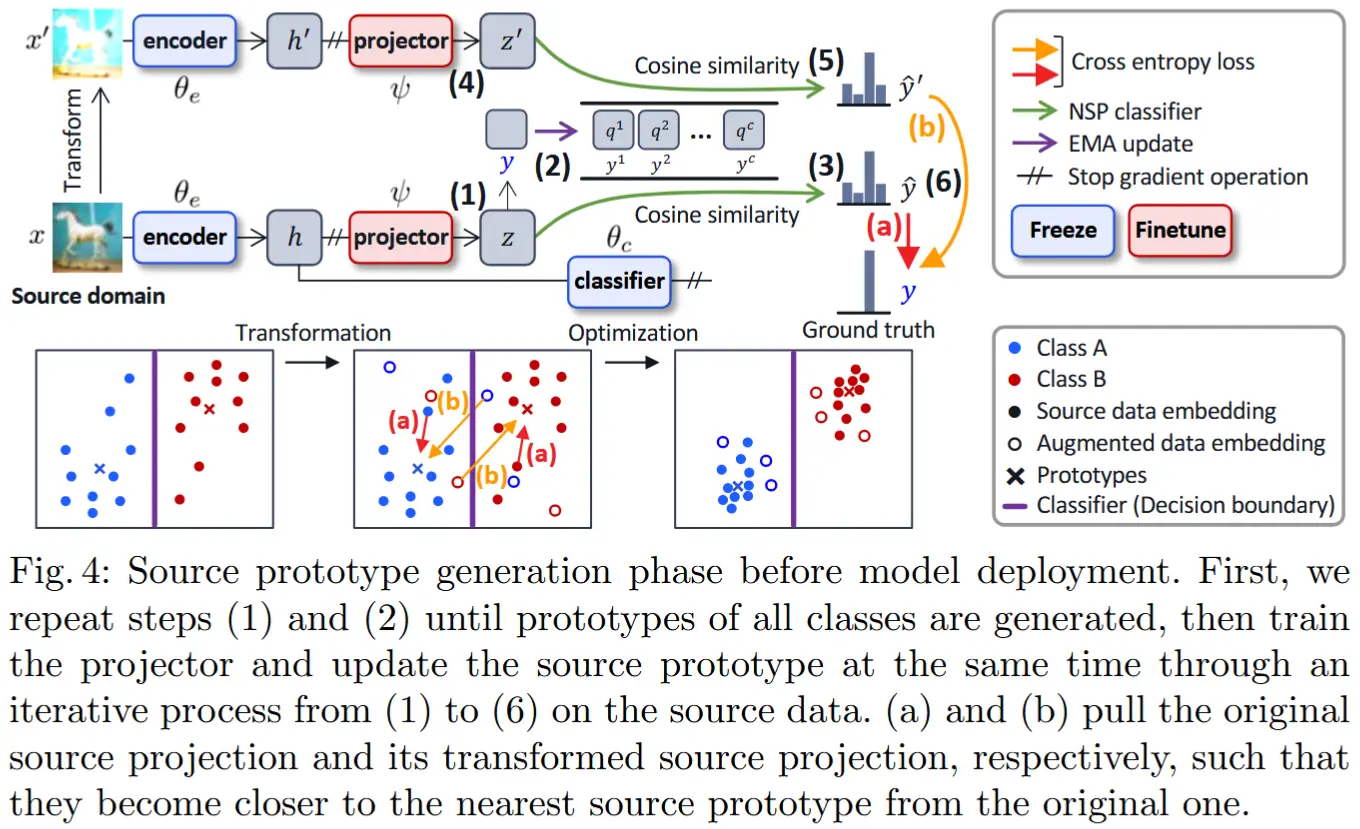
源原型被定义为每个类别上源嵌入的平均值。如图 4 所示,冻结在源数据上训练的模型 f_\theta ,并在编码器 f_{\theta_e} 后附加一个额外的投影层 h_\psi 。编码器 f_{\theta_e} 从源样本 x 推断出表示 \boldsymbol{h} ,而投影器 h_\psi 将 \boldsymbol{h} 映射到另一个嵌入空间中的投影 \boldsymbol{z} ,其中损失 \mathcal{L}_{\psi}^{\text{emb}} 被应用为 \boldsymbol{z} = h_\psi(f_{\theta_e}(x)) 。类别 k 的源原型 \boldsymbol{q}_t^k 通过指数移动平均(EMA)更新,公式如下:
其中 \boldsymbol{z}_t^k 是时间t时源样本 (x, y^k)_{k \in [1, C]} 的投影, \alpha = 0.99 ,且 \boldsymbol{q}_0^k = \boldsymbol{z}_0^k 。
NSP 分类器定义
我们定义 NSP 分类器为一种非参数分类器。它测量给定目标嵌入与所有类别的源原型之间的余弦相似度,然后生成类别概率分布 \hat{y} ,公式如下:
其中:
- S(\cdot, \cdot) 是余弦相似度函数, S(a, b) = (a \cdot b) / \|a\| \|b\| ;
- \tau 是控制分布尖锐度的温度参数;
- y^k 是第 k 类的 one-hot 真实标签向量。
此外,受近期自监督对比学习方法的启发,作者使投影器 h_\psi 学习 transformation-invariant mapping。通过 \boldsymbol{z}' = h_\psi(f_{\theta_e}(\mathcal{T}(x))) 获得变换后源样本的投影,其中 \mathcal{T}(\cdot) 表示图像变换函数。嵌入空间中的嵌入损失 \mathcal{L}_{\psi}^{\text{emb}} 包含两个交叉熵项,用于训练投影器 h_\psi ,公式如下:
其中:
- \text{CE}(p, q) = -\sum_{k=1}^C p^k \log q^k ;
- y_i 是第 i 个源样本的真实标签;
- \hat{y} 和 \hat{y}' 分别表示 NSP 分类器对源样本投影 \boldsymbol{z} 和其变换后的投影 \boldsymbol{z}' 的输出。
如图 4 所示,优化嵌入损失鼓励投影器 h_\psi 学习一种映射,使得同一类别的投影更接近,同时将源原型彼此推远。
注意上面全部的步骤都是用源域样本的warm-up过程,下面才开始TTA过程。
测试时辅助任务损失
一旦生成源原型并训练好投影层后,我们可以部署模型,并在未标注的在线数据上联合优化主任务和辅助任务。辅助任务损失 \mathcal{L}_{\theta_e}^{\text{aux}} 包含两个目标函数:基于 NSP 分类器预测 \hat{y} 的熵目标 \mathcal{L}_{\theta_e}^{\text{aux\_ent}} ,以及鼓励模型编码器 f_{\theta_e} 学习 transformationinvariant mappings 的自监督损失 \mathcal{L}_{\theta_e}^{\text{aux\_sel}} , 公式如下:
其中 \lambda_s 表示自监督损失项的重要性。与公式 (3) 类似,熵目标通过使用 NSP 分类器对目标样本的预测熵构建,公式为:
其中:
- N 是批量大小;
- \lambda_{a_1} 和 \lambda_{a_2} 表示每一项的重要性;
- H(p) = -\sum_{k=1}^C p^k \log p^k ;
- \bar{y} = \frac{1}{N} \sum_{i=1}^N \hat{y}_i 。
自监督损失应用于 NSP 分类器对变换后目标样本的预测 \hat{y}' ,公式为:
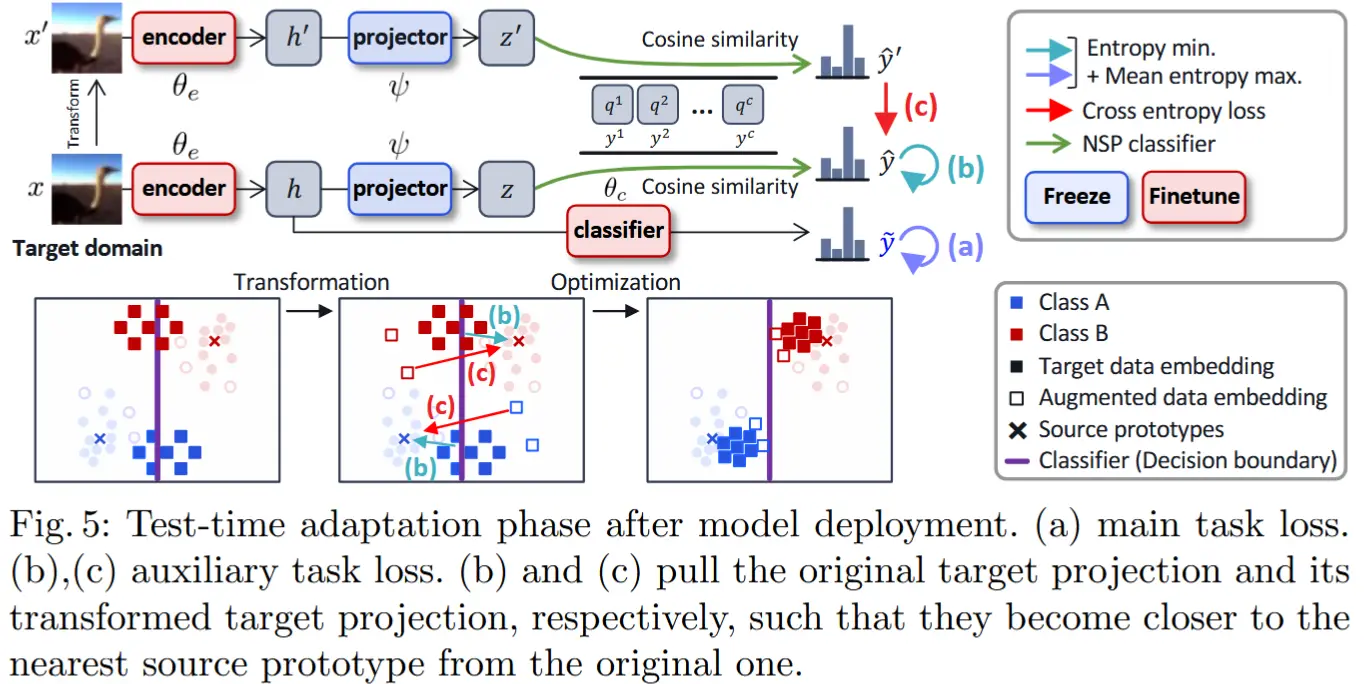
如图 5 所示,熵目标函数(图 5(b))将目标样本的投影 \boldsymbol{z} 拉近到其最近的源原型,而自监督目标(图 5(c))则鼓励变换后目标样本的投影 \boldsymbol{z}' 接近相同的 \boldsymbol{z} 。
3 实验
不展示了,只介绍一下用于理解论文的实验细节。
- 图像变换方面,作者使用了颜色失真、随机灰度、高斯模糊、随机裁剪和随机水平翻转。
- 在测试时使用目标域数据的批统计信息(batch statistics) ,而不是使用运行估计值(running estimates)。
- 投影层(projector)的训练轮数设为 20,公式 (2) 中的样本数量 N=1024。
- 投影层可以配置为单层或多层感知机(MLP)。该 MLP 结构由以下部分组成:一个线性层、批归一化、ReLU 激活函数、最后一个输出维度为 512 的线性层。(作者在消融实验部分展示了不同架构投影层的影响)