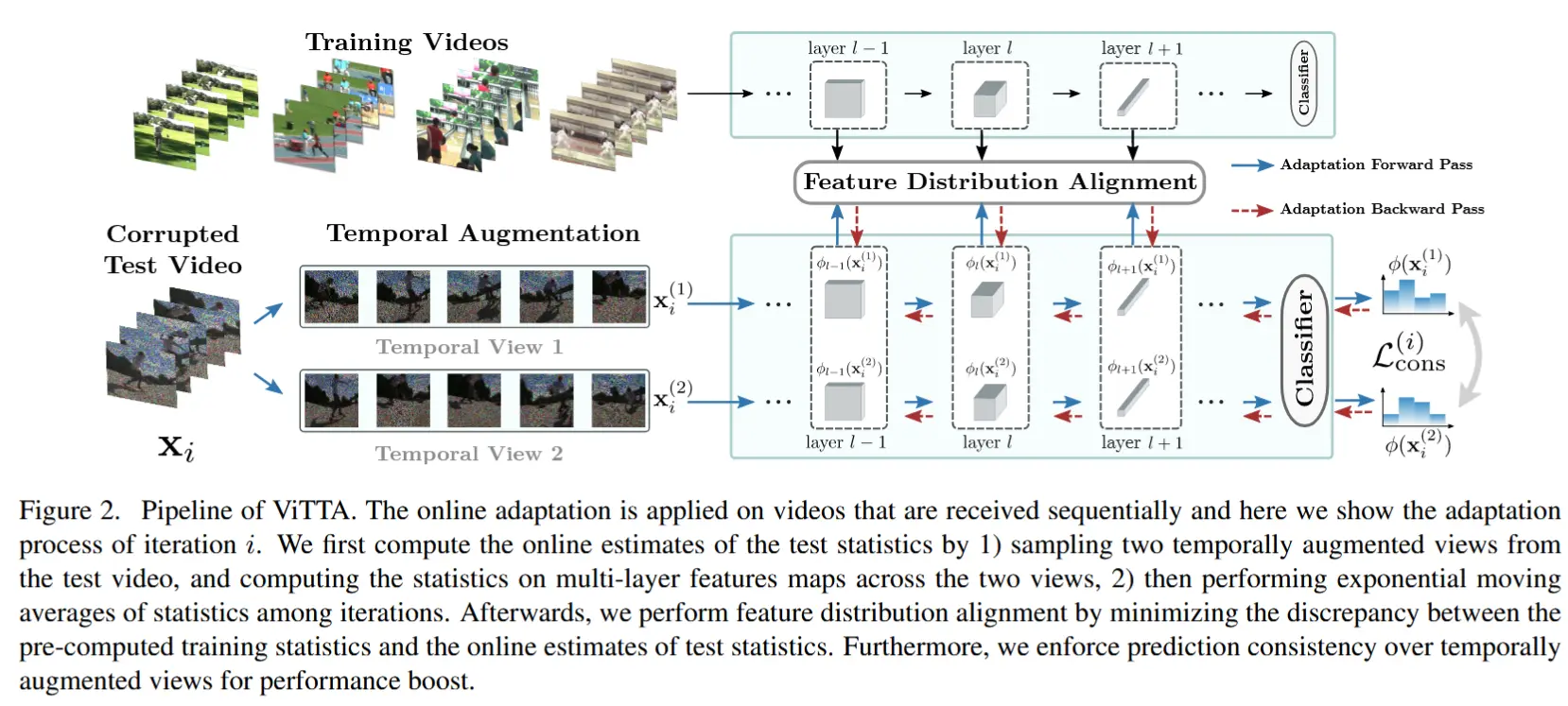
• 论文-《ENTROPY IS NOT ENOUGH FOR TEST-TIME ADAPTATION: FROM THE PERSPECTIVE OF DISENTANGLED FACTORS》
• 代码 - Github
• 关键词 - test-time adaptation、多模态、ICLR spotlight

摘要

• 问题介绍 TTA
  • 测试时适应（TTA）通过对预训练的深度神经网络进行微调以适应未见过的测试数据。
  • TTA的主要挑战是在在线更新期间对整个测试数据集的访问受限，从而导致错误累积。
  • 为了缓解这一问题，TTA方法利用模型输出的熵作为一种置信度度量，旨在确定哪些样本引起错误的可能性较低。
• 本文工作
  • 通过实验研究，观察到在有偏场景下，熵作为TTA的置信度度量并不可靠，并从理论上揭示了这是由于忽视了数据中潜在解耦因素对预测的影响。
  • 基于这些发现，作者提出了一种新的TTA方法，名为“Destroy Your Object”（DeYO），该方法利用一种新提出的置信度度量——伪标签概率差（PLPD）。
  • PLPD通过测量应用目标破坏性变换前后预测之间的差异来量化目标形状对预测的影响。
  • DeYO包括样本选择和样本加权，同时使用熵和PLPD。
  • 为了实现鲁棒的适应，DeYO在预测时优先考虑主要包含形状信息的样本。

1 引言

• 三种应对分布偏移的研究领域
  • 域泛化（domain generalization , DG）：旨在训练对任意分布偏移具有鲁棒性的模型。
  • 无监督域适应（unsupervised domain adaptation, UDA）：寻求目标域中与标签无关的域不变信息。
  • 测试时适应（test-time adaptation, TTA）：应对测试时分布偏移，在推理后立即利用每个数据点进行一次适应。

• 前人工作总结
  • 由于无法同时访问整个测试数据，TTA难以准确估计整个测试数据的分布。这导致预测不准确，将这些不准确的预测纳入模型更新会引发模型中的错误累积（Arazo等，2020）。
  • 因此，利用那些不易被错误预测的样本以减少错误累积至关重要。先前的研究（Geifman等，2019a；Lee等，2022）采用了置信度度量的概念，旨在确定可信样本。
  • 目前，最大softmax概率（Sohn等，2020）和熵（Saito等，2020），利用模型预测，是无标签任务中最常用的置信度度量。一些TTA方法还提出了基于熵的样本选择方法以识别可信样本（Niu等，2022；2023）。

• 问题：熵作为置信度度量能否在各种分布偏移下可靠地识别可信样本？
  • 作者发现当数据集中存在严重的虚假相关性偏移（spurious correlation shift, Beery等，2018）时，熵的可靠性大幅下降。
  • 为证明这一观察，作者从Wiles等（2022）的研究中汲取灵感，并通过引入输入的潜在解耦因素阐明了为何单独使用熵作为适应依据并不可靠。
• 基于上述观察
  • 作者提出了一个理论命题，用于识别有害样本，即那些在适应过程中降低模型判别能力的样本。
  • 理论：如果某个样本的预测更多受到仅在训练时与标签正相关的因素（TRAin-time only Positively correlated with label, TRAP）（例如背景、天气）的影响，而非通常与标签正相关的因素（Commonly Positively-coRrelated with label, CPR）（例如结构、形状）的影响，即使其熵较低，该样本也是有害的。
  • 原因：TRAP因素提升了训练性能，但由于与标签的相关性符号存在差异，降低了推理性能。如果预测主要依赖于TRAP因素，则在分布偏移下出现错误预测的风险较高。

• DeYO
  • 该方法利用本文提出的置信度度量 -- 伪标签概率差 PLPD 来识别熵无法检测到的有害样本。
  • DeYO使用一种单一的图像变换，该变换扭曲目标的形状，而形状是人类视觉感知的基本元素（Geirhos等，2019），并被视为具有代表性的CPR因素。
  • PLPD通过测量应用变换后伪标签概率的下降程度来量化CPR因素对模型预测的影响。较高的PLPD值表明CPR因素对模型预测的影响较大。
  • DeYO包含两个关键过程：样本选择和样本加权。
  • 通过将PLPD作为额外的选择标准，模型在相同的熵水平下选择更明显基于CPR因素的样本进行更新。因此，为了强调高置信度样本对模型更新的影响，为低熵且高PLPD值的样本赋予更大的权重。

核心贡献：证明了单独使用熵作为置信度度量在TTA中是不够的，即使是（极）低熵样本也可能降低TTA的性能。作者提出了新的置信度度量 -- PLPD和熵，PLPD通过应用于目标的破坏性变换引起的模型预测变化来检查CPR因素的影响。

2 重新审视TTA：从解耦因素的视角出发

• 第2节通过以下小节表明熵对于TTA而言是不够的：
  • 2.1节，展示了研究熵不可靠性的观察结果，并阐明了其固有特性。
  • 2.2节，提供了初步概念和必要的符号以进行进一步分析。
  • 2.3节，深入探讨了为何仅依赖熵作为置信度度量可能并不可靠的原因。
    
    

2.1 动机观察

• 为了提供与虚假相关性偏移相关的实证结果，作者在Waterbirds（Sagawa等，2020）上对熵进行了分析。
  • 该基准允许操纵类别与背景之间的虚假相关性偏移程度，并根据类别和背景类型分为四类。
  • 值得注意的是，如图2(a)所示，观察到在表现最差的组中，熵值低于第一四分位数的样本预测准确率比其他区间更低。 这一观察结果表明，基于熵的样本选择应用于适应可能会导致性能下降。
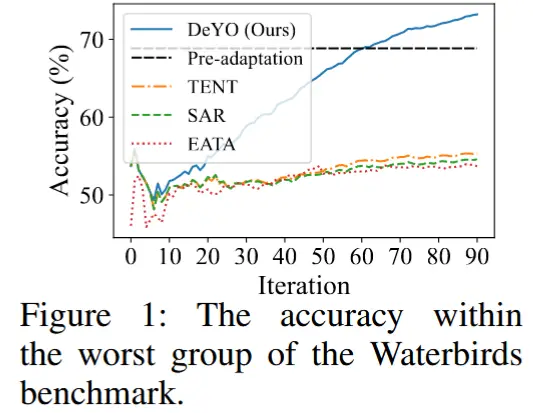
  • 当在Waterbirds基准上应用基于熵的适应时，如图1所示，其性能甚至低于适应前的模型。

• 为了直观地研究极高置信度下正确样本与错误样本之间的差异，作者在图2(b)和(c)中使用了Grad-CAM（Selvaraju等，2017）。
  • 结果显示，正确样本主要关注鸟类（目标对象），而错误样本相对更关注背景（虚假特征）。
  • 理论上，Zhou等（2021）证明了即使在仅有输入分布偏移（即协变量偏移）的情况下，深度模型也会学习训练数据中存在的虚假特征。因此，在分布偏移下，仅依赖熵可能并不始终可靠，因为它无法区分模型是否关注虚假特征。

2.2 基础知识

在 TTA 中，有一个在训练集 ​\mathcal{D}^{\text{train}} = \{(\mathbf{x}_i^{\text{train}}, y_i^{\text{train}})\}_{i=1}^{N^{\text{train}}} 上训练的模型 ​M_{\theta}，其参数为 ​\theta = \{\theta_i\}_{i=1}^{|\theta|}，其中 ​\mathbf{x}_i^{\text{train}} \in \mathcal{X}^{\text{train}} 且 ​y_i^{\text{train}} \in \mathcal{Y}。TTA 的目标是利用测试数据 ​\mathcal{D}^{\text{test}} = \{(\mathbf{x}_i^{\text{test}}, y_i^{\text{test}})\}_{i=1}^{N^{\text{test}}} 成功地对 ​M_{\theta} 进行适应，其中 ​\mathbf{x}_i^{\text{test}} \in \mathcal{X}^{\text{test}} 且 ​y_i^{\text{test}} \in \mathcal{Y}。在适应过程中，无法访问 ​y^{\text{test}}。相反，现有的 TTA 方法通过最小化 ​\text{Ent}_{\theta}(\mathbf{x}^{\text{test}}) 来更新 ​\theta，其中 ​\text{Ent}_{\theta}(\mathbf{x}^{\text{test}}) 是 ​\mathbf{x}^{\text{test}} 的熵。

其中 ​\mathbf{p}_{\theta}(\mathbf{x}) = \text{softmax}(M_{\theta}(\mathbf{x})) = (\mathbf{p}_{\theta}(\mathbf{x})_1, \dots, \mathbf{p}_{\theta}(\mathbf{x})_C) \in \mathbb{R}^C 是模型在输入 ​\mathbf{x} 上的输出概率，​C 是类别的数量。

受 Wiles 等（2022）的启发，假设对于每个输入 ​\mathbf{x}，存在一个解耦的潜在向量 ​\mathbf{v}(\mathbf{x}) = (v_1(\mathbf{x}), \dots, v_{d_v}(\mathbf{x})) \in \mathcal{V}，其中 ​v_i(\mathbf{x}) 被称为 ​\mathbf{x} 的第 ​i 个因素。为了方便起见，将交替使用 ​\mathbf{v} 和 ​\mathbf{v}(\mathbf{x})，假设 ​v_i \in [0, 1]，并专注于二分类问题，其中 ​y \in \{-1, 1\}。

首先定义两个值：​\text{corr}_i^{\text{train}} 和 ​\text{corr}_i^{\text{test}}，其中 ​\text{corr}_i^{\text{train}} = \text{corr}(y^{\text{train}}, v_i^{\text{train}}) 是训练标签 ​y^{\text{train}} 与对应于 ​\mathbf{x}^{\text{train}} 的第 ​i 个因素 ​v_i^{\text{train}} 之间的相关性，而 ​\text{corr}_i^{\text{test}} = \text{corr}(y^{\text{test}}, v_i^{\text{test}}) 是对应于 ​\mathbf{x}^{\text{test}} 的相关性。然后，可以基于 ​\text{corr}_i^{\text{train}} 和 ​\text{corr}_i^{\text{test}} 将 ​\mathbf{v} 分为四个分区：

总结：作者将输入x解耦成多个潜在向量 ​v_i ，并分别计算训练集和测试集中标签与潜在向量 ​v_i 的相关性，根据相关性将 v 分成四个分区。

2.3 熵 is not enough

在本小节中，从解耦因素的角度验证了单独使用熵作为置信度分数的不足之处。

假设 ​M_{\theta} 是一个线性分类器，然后，参数 ​\theta 对应于四个分区 ​\{\theta_{pp}, \theta_{pn}, \theta_{np}, \theta_{nn}\}，分别与 ​\{\mathbf{v}_{pp}, \mathbf{v}_{pn}, \mathbf{v}_{np}, \mathbf{v}_{nn}\} 对应。然后，可以将 logit ​a_{\theta}(\mathbf{x})、概率标量输出 ​\mathbf{p}_{\theta} 和伪标签 ​\hat{y} 表达如下：

其中 ​\sigma(\cdot) 是 sigmoid 函数。然后，在 TTA 的情况下，以下命题成立。

命题 1. 假设有一个预训练的线性分类器 ​M_{\theta}，其输入为样本 ​\mathbf{x} 的潜在解耦因素 ​\mathbf{v}(\mathbf{x})。将一个用于适应时会减少类间平均对数似然差异的样本定义为有害样本。如果满足以下条件，则测试集中的样本 ​\mathbf{x} \in \mathcal{X}^{\text{test}} 是一个基于熵最小化损失进行适应的有害样本：

其中 ​\mathcal{X}_y^{\text{test}} = \{\mathbf{x} | (\mathbf{x}, \mathbf{y}) \in \mathcal{D}^{\text{test}}, \mathbf{y} = y\}，且 ​y \in \{1, -1\}。

对于有害样本的识别，核心在于公式（5），该公式从左至右由三个部分组成：

1） 第一个是伪标签 ​\hat{\mathbf{y}}，由公式 4 定义

2） 第二个是潜在解耦因素 ​\mathbf{v}(\mathbf{x}) ，表示 x 的特征分解结果。

3）第三个是期望值的差，表示正类和负类之间潜在解耦因素的差异，即 正类测试集上的潜在解耦因素的期望值 - 负类测试集上的潜在解耦因素的期望值。

下面的证明是实在看不懂，直接翻译了.......

在本节的其余部分，将通过命题 1 解释为什么低熵的样本可能是有害的。

根据解耦因素分区的定义，最优参数 ​\theta^* 在训练数据上的分区满足 ​\theta_{pp}^*, \theta_{pn}^* > 0，​\theta_{np}^*, \theta_{nn}^* \leq 0。由于 ​\theta_i 在适应的早期阶段与 ​\theta_i^* 具有相同的符号，对于具有高置信度伪标签 ​\hat{y} = 1 的 ​\mathbf{x}，满足：

换句话说，​\mathbf{v}_{np} 和 ​\mathbf{v}_{nn} 的元素倾向于变为零，而 ​\mathbf{v}_{pp} 和 ​\mathbf{v}_{pn} 成为组成 ​\mathbf{x} 的主导因素。将 ​\mathbf{v}_{pp} 称为与标签共同正相关的（Commonly Positively-coRrelated，CPR）因素，将 ​\mathbf{v}_{pn} 称为仅在训练时与标签正相关的（TR Ain-time only Positively-correlated，TRAP）因素。​\mathbf{v}(\mathbf{x}^{\text{test}}) 的期望值遵循由定义的 CPR 和 TRAP 因素的关系：

对于具有高度置信度 ​\hat{y} = 1 的 ​\mathbf{x}，公式 (5) 可以近似为：

在公式 (7) 中，根据公式 (6)，与 CPR 因素相关的 (7.a) 部分变为正值，而与 TRAP 因素相关的 (7.b) 部分变为负值。因此，​\mathbf{x}^{C \ll T}，即 ​\| (7.\text{a}) \| \ll \| (7.\text{b}) \| 的 ​\mathbf{x}，即使在熵方面表现出高置信度，也是一个有害样本。这表明，仅依赖压缩信息（表示为 ​\theta \cdot \mathbf{v}）的熵无法通过其值区分有害样本。如果适应过程不考虑 CPR 和 TRAP 因素，在极端情况下，两个类别的对数似然之间的相对顺序甚至可能发生改变，导致完全错误的预测。因此，作者旨在引入一种新的置信度度量，通过避免 TRAP 因素并纳入 CPR 因素来应对测试数据集中的各种分布偏移。

3 方法论

• DeYO
  • DeYO 引入了新提出的伪标签概率差（Pseudo-Label Probability Difference, PLPD）分数，以考虑CPR因素对模型预测的影响，特别是目标形状信息的影响。
  • 通过整合PLPD分数（该分数强化对CPR因素的考虑，同时抑制TRAP因素），缓解了仅依赖熵所带来的局限性。
  • DeYO由基于PLPD分数的样本选择（第3.1节）和样本加权（第3.2节）组成

3.1 样本选择

正如第2节所述，当训练集 ​\mathcal{X}^{\text{train}} 和测试集 ​\mathcal{X}^{\text{test}} 之间存在显著的分布差异（例如虚假相关性偏移）时，熵变得高度依赖于TRAP因素，从而削弱了其可靠性。为了对分布偏移具有鲁棒性，捕获CPR因素至关重要。虽然捕获所有CPR因素具有挑战性，但作者利用了一个突出且确定的CPR因素：目标的形状信息。

通过图像变换（如像素打乱、块打乱或中心遮挡）可以融入目标的形状信息。如图3所示，每种目标破坏技术都有其独特的特性。对于像素打乱，图像的平均颜色得以保留，但目标和背景都变得难以辨认。块打乱会破坏目标的形状，但通过局部块保留了局部信息。中心遮挡则保留了背景信息。然而，当目标未居中或特别大时，可能无法完全破坏目标的形状。 作者对这三种技术进行了实验，如第4.3节所示，观察到块打乱表现最佳，因为它仅消除了目标的形状信息，而不会影响其他成分。

提出了一种基于熵和PLPD的新样本选择策略，以识别用于模型更新的可靠样本。采用以下样本选择标准：

其中：

• ​\mathbf{x} 是输入，​\mathbf{x}' 是经过块打乱的输入。
• ​\tau_{\text{Ent}} 和 ​\tau_{\text{PLPD}} 分别是熵和PLPD的预定义阈值。
• ​\hat{y} = \arg\max \mathbf{p}_{\theta}(\mathbf{x}) 是通过对 ​\mathbf{x} 的预测估计的伪标签。

在第2节假设下，PLPD可以表示为：

这表明，基于熵的样本选择并未考虑CPR因素对预测的影响，因为它依赖于单一预测。相比之下，PLPD通过量化预测差异来评估CPR因素的影响，这种差异取决于形状信息的存在与否。因此，使用PLPD补充了可能主要受TRAP因素影响的基于熵的样本选择。

开销：这一选择过程仅需要一次额外的前向传播，开销可忽略不计，因为不需要额外的反向传播。

3.2 样本加权

DeYo 方法通过样本加权使识别出的样本对模型更新做出不同的贡献。

具体而言，图4中的区域1、区域2和区域3中的样本被排除，而区域4中的样本对模型更新的贡献则根据其可靠性有所不同。形式上，表示权重函数 ​\alpha_{\theta}(\mathbf{x}) 如下：

其中：

• ​Ent_0 是一个归一化因子。
• 第一项是基于熵的权重项，已在现有方法（Wang等，2021b；Niu等，2022）中使用，并且在各种基准上通常有效。然而，基于观察到的不可靠性，作者引入了一个额外的基于PLPD的权重项。该项随着预测更多地依赖于目标形状而赋予更大的权重。
• 每个权重项都是有效的，但将它们结合在一起会带来更好的性能。

3.3 DeYO 的整体流程

DeYO 通过仅利用属于 ​S_{\theta}(\mathbf{x})（公式8）的样本进行样本选择，并计算样本权重 ​\alpha_{\theta}(\mathbf{x})（公式10），以优先考虑那些预测特别依赖于 CPR 因素的样本。然后，整体加权样本损失由以下公式给出：

该公式结合了在样本选择和加权中基于熵和 PLPD 的项。

• DeYO 的算法

4 实验

• 五个基准数据集上进行了实验：
  • ImageNet-C （Hendrycks & Dietterich, 2019），一个知名的 TTA 基准数据集，分为 15 种损坏类型，每种类型包含 5 个严重级别；
  • ColoredMNIST 和 WaterBirds ，两个评估极端虚假相关性偏移对性能影响的基准数据集；
  • ImageNet-R （Hendrycks 等, 2021）和 VisDA-2021 （Bashkirova 等, 2022），这两个基准数据集涵盖了由于从不同风格领域（例如卡通、素描等）收集的数据而导致的多样化分布偏移，用于评估更具挑战性的复杂测试场景。
• 测试场景
  • 遵循 Wang 等（2021a）提出的温和场景以及 Niu 等（2023）建议的三种复杂测试场景。此外，还提出了新的偏向场景，利用 ColoredMNIST 和 WaterBirds 数据集，涵盖严重的分布偏移。
• 模型选择
  • ResNet-18-BN 、 ResNet-50-BN（批归一化）、ResNet-50-GN（组归一化）以及 VitBase-LN（层归一化）

4.1 主要结果

• 在温和场景中的比较
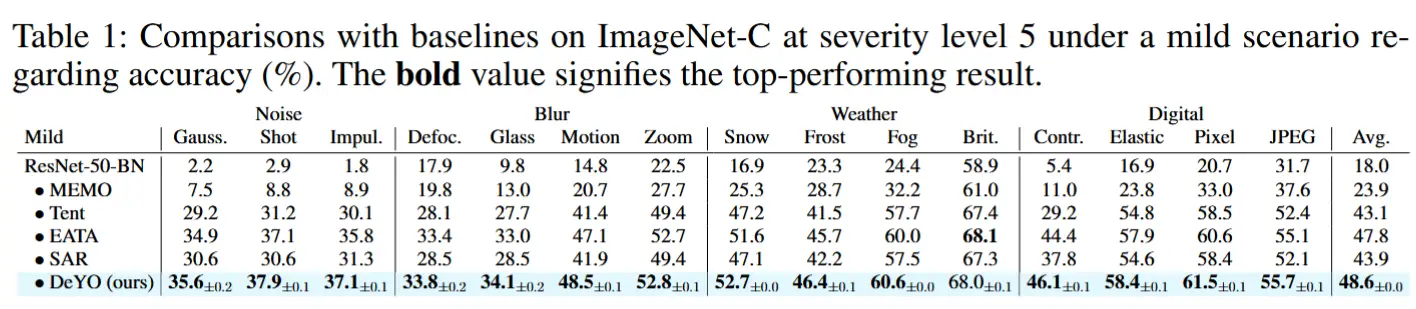
  • ImageNet-C 的对比结果如表 1 所示

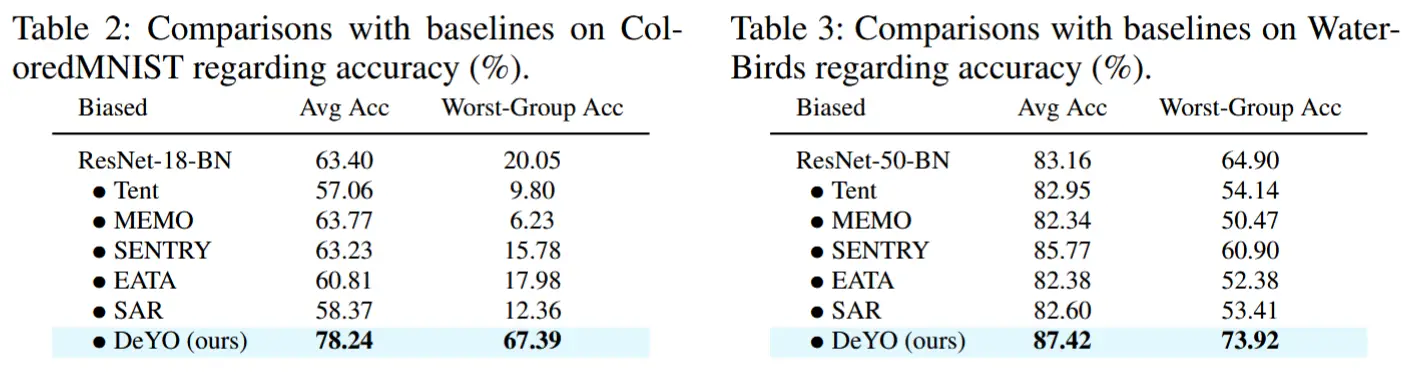
• 在偏向场景中的比较
  • 如表 2 和表 3 所示，在固有包含虚假相关性偏移的 ColoredMNIST 和 WaterBirds 数据集上，DeYO 分别实现了 17.43% 和 4.47% 的显著性能提升。

• 在复杂场景中的比较
  • 在复杂的现实场景中，测试数据可能以更不可预测的方式到达。因此，SAR 提出了三种更贴近现实的测试场景。
  • i) 在线不平衡标签分布偏移
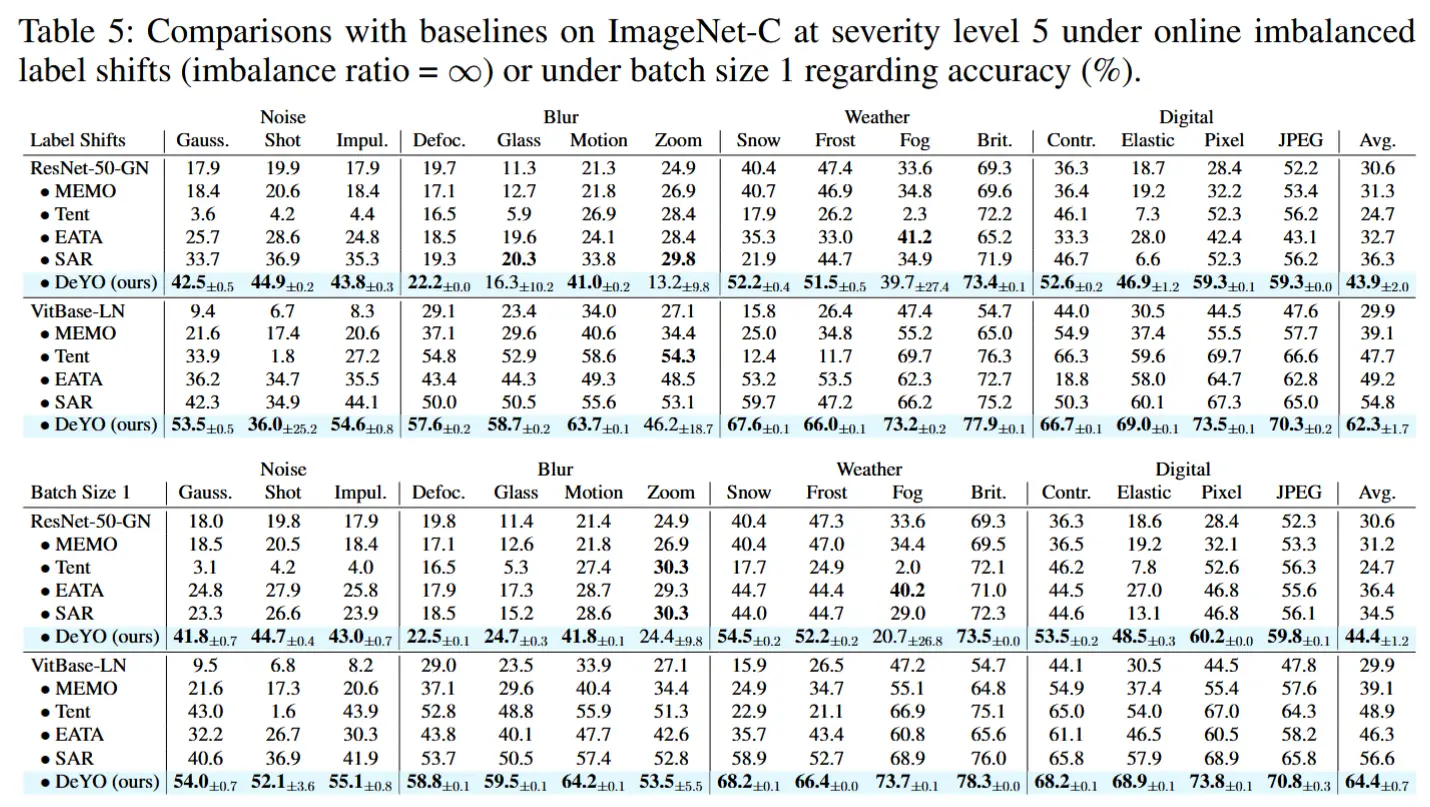
    • 在类别不平衡比率为无穷大的情况下比较了基线方法和 DeYO 的性能，如表 5 所示。
  • ii) 批量大小为 1
    • 如表 5 所示，即使在单个测试样本的情况下，DeYO 仍然表现出卓越的性能。
  • iii) 混合分布偏移
    • 评估了在严重级别为 5 和 3 的 15 种损坏类型的混合情况下的性能，如表 4 所示。尽管性能提升可能不如前两个复杂测试场景那么显著，但 DeYO 仍然表现出最优越的性能。

4.2 PLPD 的作用与效果

• 关于虚假相关性的讨论
  • 从前面的表3中可以看出，在具有极端虚假相关性偏移的 Waterbirds 基准上，DeYO 的表现优于其他基线方法，侧面印证了虚假相关性的有效性。
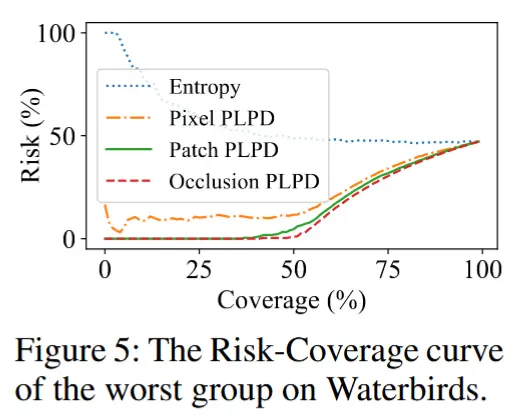
  • 为了分析 PLPD 作为一种置信度度量的效果，作者使用了 Risk-Coverage 曲线（Geifman 等, 2019b），其中风险表示错误率，覆盖率表示输入的比例。根据 Ding 等（2020）的研究，一种可靠的置信度度量应表现出较低的风险-覆盖率曲线下面积（AURC）。如图 5 所示，在最差组的 RC 曲线中，熵相比 PLPD 的变体产生了更大的 AURC，表明其作为置信度度量的可靠性有限。

• 被过滤样本的性能
  • 研究 PLPD 是否能够在相对弱虚假相关性偏移的数据集（例如 ImageNet-C）中利用熵可能忽略的信息。
  • 这一分析展示在图 6 中，图中显示了图 4 （3.3节）各区域在适应前模型上的准确率。在 ImageNet-C 数据集上，比较严重级别为 5 的高斯噪声损坏下相同熵水平的区域准确率时，可以明显看出，具有高 PLPD 的区域 2 和区域 4 的准确率分别高于区域 1 和区域 3。这一结果表明，即使在虚假相关性偏移较弱的基准数据集中，PLPD 也能通过利用熵无法捕捉到的信息来识别更可靠的样本。

4.3 超参数和消融实验

• 超参数敏感性
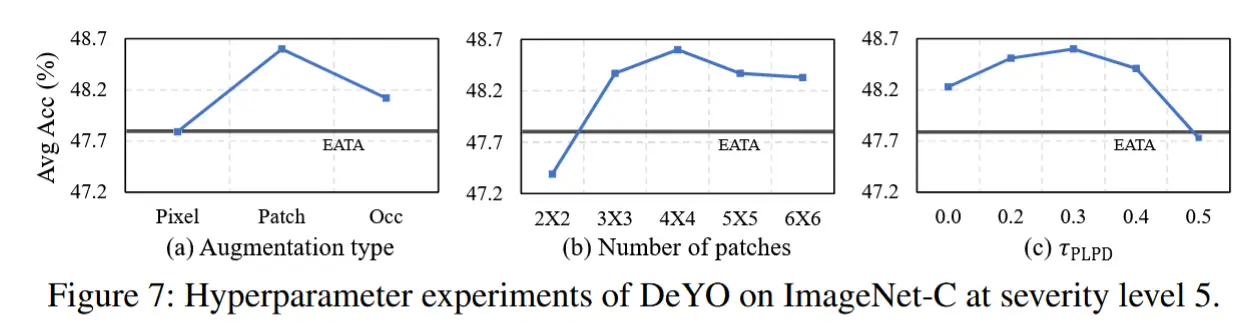
  • 变换方法选择：作者实验了三种变换方法（像素打乱、块打乱和中心遮挡）来扭曲目标形状（​\mathbf{x}'）。其中，如图 7(a) 所示，仅消除形状信息而保留其他细节的块打乱表现最佳。
  • 块数量的影响：在选择块打乱作为变换时，作者进一步测试了图像大小为 ​224 \times 224 的不同块数量。如图 7(b) 所示，块数量为 ​4 \times 4 时性能最高，并且从 ​3 \times 3 块数量开始，始终优于 EATA。
  • PLPD 阈值 ​\tau_{\text{PLPD}} 的影响：DeYO 在采样选择过程中需要设置阈值 ​\tau_{\text{PLPD}}（见图 7(c)）。较高的 ​\tau_{\text{PLPD}} 会导致移除更多样本，可能阻碍足够的适应知识获取。观察到，当 ​\tau_{\text{PLPD}} \in [0.2, 0.3] 时，DeYO 表现出色。

• 消融研究
  • 各组件的重要性评估：在 ImageNet-C 数据集（严重级别 5）上进行了消融研究，以评估 DeYO 各组件的重要性。在其他条件相同的情况下，使用 PLPD​_{\theta} 的性能优于熵 Ent​_{\theta}，并且同时使用 PLPD​_{\theta} 和 Ent​_{\theta} 时性能最佳。
  • 偏向场景中的表现：在偏向场景（WaterBirds 数据集）上也进行了实验。与 ImageNet-C 的趋势类似，但在 WaterBirds 中，仅在 ​S_{\theta} 中使用 PLPD​_{\theta} 的表现优于同时使用 PLPD​_{\theta} 和 Ent​_{\theta}。这验证了作者的观察：在严重的分布偏移下，熵的可靠性显著下降。

5 总结

与普遍共识相反，我们从理论上证明了，即使在适应过程中使用极低熵样本，如果不考虑解耦因素的影响，性能仍可能下降。基于这一理论证据，我们提出了 DeYO，这是一种结合了我们的置信度度量 PLPD 和熵的 TTA 方法，其中 PLPD 旨在考虑目标形状信息的影响。据我们所知，DeYO 是首个在温和场景和复杂场景中均表现出最佳性能的 TTA 方法，在各种分布偏移下均显示出显著的性能提升。