- 论文 - 《L-TTA: Lightweight Test-Time Adaptation Using a Versatile Stem Layer》
- 代码 - Github
- 关键词 - Neurips2024、TTA、高效、图像分类
摘要
- 研究背景
- 测试时自适应 TTA 用于通过仅使用目标域的未标记数据来将深度学习模型适配到真实世界。
- 局限:许多关于TTA的研究都集中在最小化熵的目标上。然而,这种方法需要在整个模型中进行前向和反向传播,并且由于完全依赖熵而无法充分利用数据。
- 本文工作
- 本研究摆脱了传统以最小化熵为核心的思路。
- 独特地重塑了模型的初始层(即第一层),转而强调最小化一种新的学习准则——不确定性。该方法只需极少量地涉及模型的主干部分,仅由初始层参与TTA过程。这显著减少了训练所需的内存,并能够通过最少的参数更新快速适配到目标域。
- 此外,为了最大化数据的利用效率,初始层对输入特征应用离散小波变换,提取多频域信息,并专注于最小化各个频域的不确定性。
- 实验性能
- 使用ResNet-26和ResNet-50模型,在CIFAR-10-C、ImageNet-C和Cityscapes-C等基准数据集上的TTA性能表现卓越,同时使用了极少的内存,充分展现了其鲁棒性。
1 介绍
-
域偏移问题
- 定义:如何让训练好的模型适应数据分布的多样性。
- 常见解决方案:域适应 DA 和 域泛化 DG。
- 这两者的区别在于是否能够访问目标域的数据。具体来说,DA可以访问所有域,但在目标域中只能使用未标记的数据;而DG仅能在源域中进行训练。
-
测试时自适应
- 通常,TTA研究关注两个关键观察点:
- (1) 当域偏移发生时,批归一化(Batch Normalization, BN)统计量的变化。
- (2) 在模型被训练为最小化预测熵的情况下,适配的可能性。
- 尽管当前研究提高了适配性能,但它们仍受限于高昂的训练成本和内存消耗。
- 通常,TTA研究关注两个关键观察点:
-
作者将这些研究的基本问题总结为以下三个主要方面:
- (1) 通过整个模型的前向传播来获取熵值会带来计算成本;
- (2) 为了实现反向传播,必须付出巨大的代价才能到达初始归一化层;
- (3) 缺乏确保数据独立性的方法可能导致学习偏差。如果噪声数据未被识别,模型可能会朝错误方向学习;即便识别了噪声数据,这一过程也会增加训练时间。
-
研究假设
- 本文基于一个假设展开:微调第一个卷积(CONV)层(即所谓的stem层 )可以显著影响TTA的结果。
-
本文设计
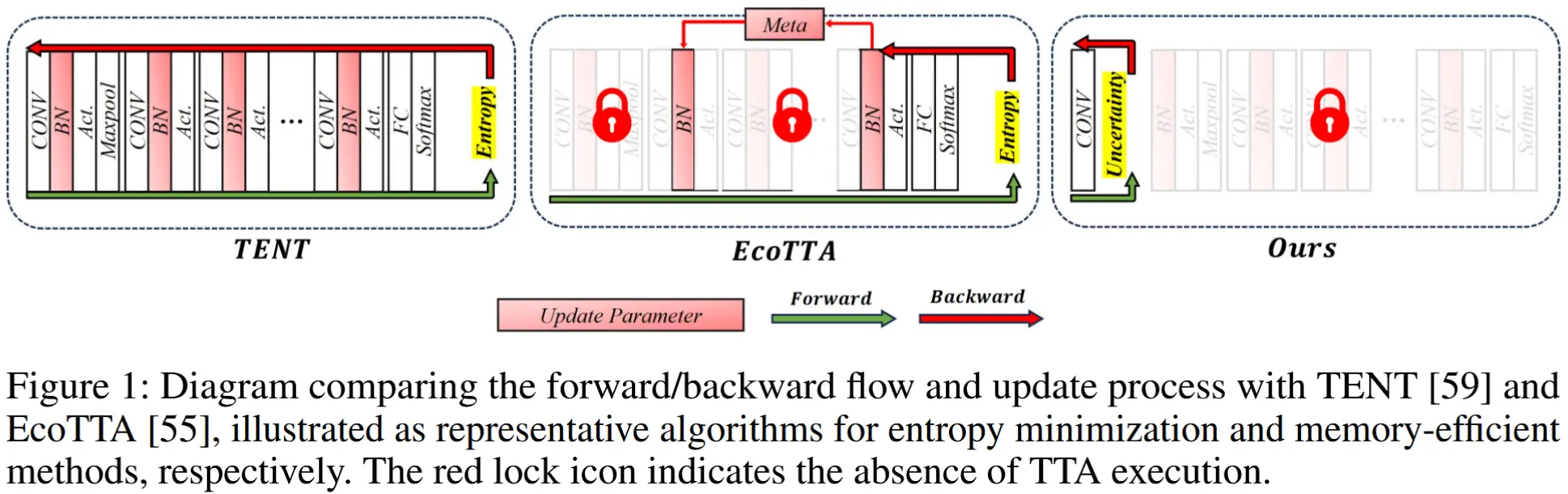
- 轻量级TTA的实现 :通过最小化从高斯通道注意力层(Gaussian Channel Attention Layer, GCAL)中提取的中间特征在通道注意力上的不确定性,而非采用熵最小化策略,从而实现轻量级TTA。如图1所示,此方法省略了除重构stem层以外的所有参数的前向和反向传播过程。以该stem层作为支点,无需存储额外梯度,从而实现了最快的训练速度并显著降低了训练成本。
- DEL的集成以最大化单个数据点的训练效果 :在stem层中集成了域嵌入层(Domain Embedding Layer, DEL),利用其中的二维离散小波变换(2D Discrete Wavelet Transform, 2D DWT)高效收集域不变的边缘信息,并通过在CONV操作之前提供多视角的冗余内容信息来提升模型的泛化能力。此外,将从多个频域提取的特征传递给GCAL,可以逐个计算不确定性,从而最大化数据利用率。
- 非侵入式设计 :DEL包含逆离散小波变换(Inverse DWT, IDWT),从而实现非侵入式设计。这使得其输出形状与现有stem层中CONV操作得到的中间特征形状一致。便于集成到CNN网络,高可扩展性。
2 相关工作
2.1 TTA 测试时自适应
- 非高效 TTA 方法
- BN STAT [42] 指出了跨所有域广泛存在的协变量偏移(covariate shift),并在测试时调整批归一化(BN)层的固定参数,特别是均值和方差,以应对这一问题。
- TENT [59] 提出了一种通过最小化预测熵来显著提升性能的策略,具体方法是更新每批次的统计量和仿射变换参数。
- MEMO [65] 在测试时对输入应用多种数据增强,并最小化通过模型后获得的熵的平均值(边际熵),从而展现出更好的适配效果。
- EATA [45] 在 TENT 的基础上进行了扩展,指出高熵的数据点对适配没有贡献,并提出了用于设定阈值的标准。
- SAR [46] 则进一步发展,针对现实中的混合分布变化、小批量数据以及不平衡的标签分布变化提出了改进方案。它通过将所有样本分配到同一类别来实现稳定的 TTA,并提出了一种最小化损失曲面锐度的策略。
- REALM [53] 在基于熵最小化的研究中实现了最高性能。与其他方法不同,REALM 引入了一种基于自监督学习的框架,能够在训练中包含噪声样本而不跳过它们。
- 局限:全局前向/反向传播的基本训练成本、熵最小化在评估数据是否适合用于 TTA 方面存在局限性。
- 高效 TTA 方法
- EcoTTA [55] 旨在 TTA 过程中最小化内存消耗。通过将用于 TTA 的辅助网络部分放置在主网络外部实现的。该方法确保在反向传播过程中仅传递主网络和辅助网络中的批归一化(BN)层,从而显著缩短了路径长度。这同时减少了梯度计算所需的内存以及时间消耗。
- MECTA [24] 采用了与 EcoTTA 类似的训练流程,其中模型的所有层都进行前向传播,并引入了一个专门的归一化层以最小化内存使用,尤其是在缓存中的占用。然而,它仍然依赖于 TENT 和 EATA 等方法来执行 TTA。
- DDA [17] 提出了一种直接利用生成模型将从 D_t 获得的输入投影到 D_s 的方法,而无需进行昂贵的重新训练。然而,这种方法在维护额外系统时可能会导致更高的成本,类似于数据增强所带来的开销。
2.2 DWT 离散小波变换
- 小波变换 WT 优点
- (1) 通过在多尺度上分析信号,提供了灵活的时间-频率分辨率,使其在信号处理中比傅里叶变换更为有效。
- (2) 由于小波函数具有短时性和局部化特性,WT 非常适合处理非平稳信号。
- (3) 它允许进行多级分解,直到输入图像的宽度和高度均为 2 的幂次方。这使得可以对关键信息进行高效的概括和提取。通过逆变换,原始图像可以以极高的精度重建,且信息损失最小。
- 基于这些优势,二维离散小波变换(2D DWT)[28] 常被用于在空间域中提取细节和边缘信息。
- 2D DWT 过程
- 依次对输入数据的行和列应用一维离散小波变换(1D DWT)。
- 对于 1D DWT,使用最简单的小波族,即 Haar 小波(通过卷积操作方便地实现)进行操作。
- 在第一阶段,进行水平方向分解,将单个原始特征图分为两个分量:低频分量(LFC) 和 高频分量(HFC) 。
- 在第二阶段,进行垂直方向分解,此时两个滤波器被转置。
高频分量(HFC) 是信号处理和图像处理中的一个概念,指的是信号或图像中变化剧烈的部分。这些部分通常对应于图像中的边缘、纹理、细节或噪声等信息。
低频分量(LFC) ,它主要表示图像中平滑变化的部分,包含视觉直观的信息。如整体结构或背景。
3 提出的方法
3.1 概述
- 动机:如前所述,TTA 的计算和内存成本。
- 目标
- 训练实用性 :最小化训练所需的资源(如内存和数据),以在目标域 D_t 中实现可接受的合理预测精度。
- 可扩展性 :设计为非侵入式且便于应用于基于 CNN 的任务,无需修改其他层。
- 数据利用 :最大化独立数据的可用性,即使在小批量或单一批次的情况下,也能在约束条件下实现 TTA。
- 方法:CNN 各层的顺序影响会导致不同输入图像域之间预测质量的显著变化。通过对输入图像的第一层表示进行微调,可以快速适配到目标域 D_t 。因此,不再依赖昂贵的熵计算,而是从重构的初始层中提取并最小化通道级不确定性,以实现对 D_t 的适配。
- 工作流程
- 重构的初始层包括原始卷积层以及本研究中的两个关键架构:GCAL 和 DEL。其中,DWT 和 IDWT 的过程包含在 DEL 中。
- GCAL 是唯一能够实现适配的关键架构,并以端到端的方式输出通道级注意力及其相关不确定性。与 SE 模块类似,提取的注意力是标量,并按通道逐一应用于每个特征。同时,不确定性通过负对数似然(NLL)损失进行最小化。
- 在 DEL 中,DWT 将输入特征图分解为多个频域,同时保持空间信息。此步骤在卷积操作之前执行,允许从独立数据中捕获更多样化的特征,从而更好地把握源域 D_s 和目标域 D_t 之间的差异。通过在初始层末尾执行 IDWT,特征的形状被恢复到修改前的状态。这使得初始层可以非侵入式地应用于预训练模型,并从多视角中合成重要的冗余信息以增强泛化能力。
- 在将初始层注入预训练模型进行预热的同时,联合训练它,通过合适的损失项(如交叉熵)结合从 GCAL 提取并通过 NLL 损失最小化的不确定性,以减少特定任务的预测误差。需要注意的是,由于不确定性仅在训练期间最小化,在 TTA 设置中,IDWT 后的步骤并不需要。
初始层在原文中称为stem layer。
3.2 GCAL:高斯通道注意力层
GCAL 是一个关键架构,仅通过初始层即可实现 TTA,并预测不确定性。请注意,SE 模块并未被集成到其他层中,而是端到端训练的。它动态地从中间特征中提取通道级注意力 \gamma_{\text{scale}} ,并进行重新校准。这增强了卷积层的表示能力,最终提高了预测精度。
其中,\tilde{X} 表示经过全局平均池化后获得的中间特征。权重 W_1 根据预设的超参数减少 \tilde{X} 的通道数,而 W_2 则将其扩展回原始的通道数。\sigma 和 \delta 分别表示 sigmoid 函数和 ReLU 函数。
在本研究中,SE 模块的输出 \gamma_{\text{scale}} 由高斯参数表示,即均值 \gamma_{\mu} 和方差 \gamma_{\Sigma} 。用于量化 \gamma_{\text{scale}} 不确定性的概率密度函数定义如下:
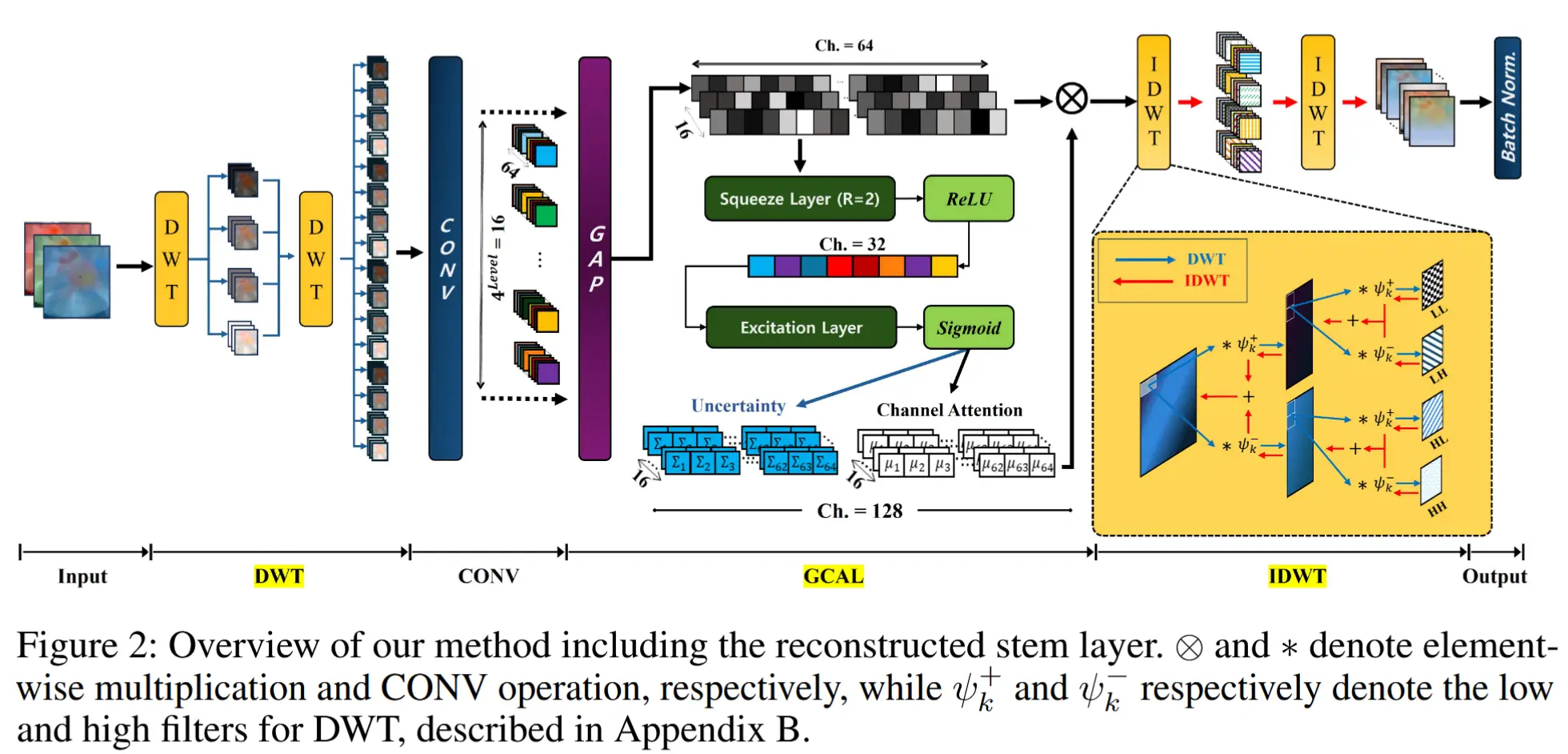
为了实现这一功能,我们在不显著改变 F_{se} 结构的情况下,通过将通道数增加 100% 来获得 \gamma_{\mu} 和 \gamma_{\Sigma} 。如图 2 所示,这两个高斯参数的定义如下:
为了执行测试时自适应(TTA),我们最小化高斯参数 \gamma_{\Sigma} ,以减少 \gamma_{\text{scale}} 的不确定性,并按通道级进行乘法操作。需要注意的是, \gamma_{\text{scale}} = \gamma_{\mu} 。然而,由于 \gamma_{\mu} 是根据输入动态确定的,在 TTA 场景下难以确定其真实值(ground-truth)。因此,我们旨在修改 SE 模块,使其主要作为 TTA 的不确定性提取器。在所有训练设置中,我们将 \gamma_{\mu} 的真实值设置为 sigmoid 函数的最大值(即 \mu_{gt} = 1),以便进行训练。基于此方法,我们重新定义负对数似然(NLL)损失,结合公式 (2) 最小化 \gamma_{\Sigma} (即不确定性):
其中, C 表示中间特征中的总通道数。公式 (4) 表示对所有通道进行不确定性最小化,这同样适用于预训练和 TTA 过程。
3.3 DEL:域嵌入层
在最近的 TTA 场景中,传统的熵最小化模型通常是通过过滤掉评估为低熵的数据来学习的。然而,与这一趋势相反,[61] 实验表明,从输入图像中提取的高频分量(HFC)有助于提高模型的泛化能力。这意味着高熵实际上对提升预测精度有显著贡献。因此,为了避免这种熵的模糊性以提高单个输入数据 x^t 的独立可用性,必须避免高熵。然而,如果不增加额外的训练成本,仅在测试时确定熵阈值和控制强度显然是具有挑战性的。
为了缓解熵的模糊性,作者提出了 DEL,它将 GCAL 和 CONV 层封装在离散小波变换(DWT)和逆离散小波变换(IDWT)层中,如图 2 所示。这将独立的 x^t 分解到多个频域,并允许对每个通道进行端到端的不确定性学习。相应地,重新定义了公式 (4) 中的不确定性损失项,如下所示:
其中, N 表示通过 DWT 分解出的频率数量。如图 3(a) 所示,DWT 层即使在分解后也能保持空间特性,而无需重构,这与常见的变换方法 [4, 51] 不同,后者在分解后通常会丢失空间信息。最后的 IDWT 层使后续层的输入形状与没有 DEL 时相同,并保持了特征的空间特性。因此,DEL 实现了非侵入式设计。

此外,作者提出了 全向分解(ODD),它可以同时对低频分量(LFC)和高频分量(HFC)加性分解。如图 3(a) 所示,当执行一次 DWT 时,可以观察到与 LFC 重叠的边缘信息仍然保留在 HFC 中。我们在保持空间特性的层次上尽可能分解边缘和噪声信息,从而能够更敏感地计算单个输入 x^t 的不确定性。此外,作为一种副作用,模型通过明确识别 HFC 中的噪声数据,进一步提升了泛化性能。
图 3(b) 可视化了我们在执行所提出的 TTA 时,LFC 和 HFC 的每个通道上的不确定性图的变化。定义 \Delta\gamma_{\Sigma} 和 \Delta\hat{\gamma}_{\Sigma} 如下:
在 \Delta\gamma_{\Sigma}^{LFC} 中,即使在执行 TTA 之前,使用 \tilde{X}_s 和 \tilde{X}_t 获得的每个通道的不确定性之间也存在明显差异。另一方面, \Delta\gamma_{\Sigma}^{HFC} 表明 F_{SE}(\cdot) 无法正确获取关于 \tilde{X}_t 的不确定性。因此,我们通过 \Delta\hat{\gamma}_{\Sigma}^{HFC} 证明了通过执行 TTA 可以正确提取不确定性。
图3(b)中,左边两个分别表示LFC和HFC使用源域特征 \tilde{X}_s 和目标域特征 \tilde{X}_t 获得的每个通道的不确定性差异,右边两个图分别表示使用TTA之后,LFC和HFC使用源域特征 \tilde{X}_s 和目标域特征 \tilde{X}_t 获得的每个通道的不确定性差异。
- 根据该图有三个结论:
- 在没有执行 TTA 的情况下,源域和目标域的低频分量之间就已经存在显著的不确定性差异。
- 仅使用 SE 模块(即不进行 TTA),无法准确捕捉目标域 \tilde{X}_t 的不确定性,特别是在高频分量上。
- 通过执行 TTA(即更新权重 \hat{W}),可以显著改善对目标域 \tilde{X}_t 不确定性的捕捉能力,尤其是在高频分量上。
4 实验
这里简单展示一下实验结果。
- 在CIFAR - 10 - C和ResNet - 26以及ImageNet - C和ResNet - 50上与之前的TTA方法进行预测误差( % )的比较

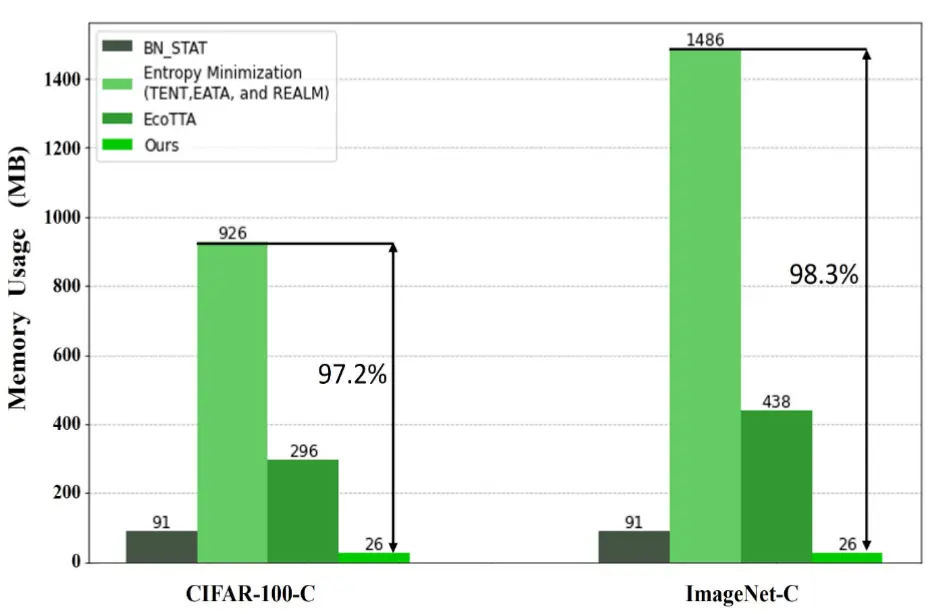
- 在CIFAR - 100 - C和ImageNet - C数据集上比较单次迭代的内存使用情况
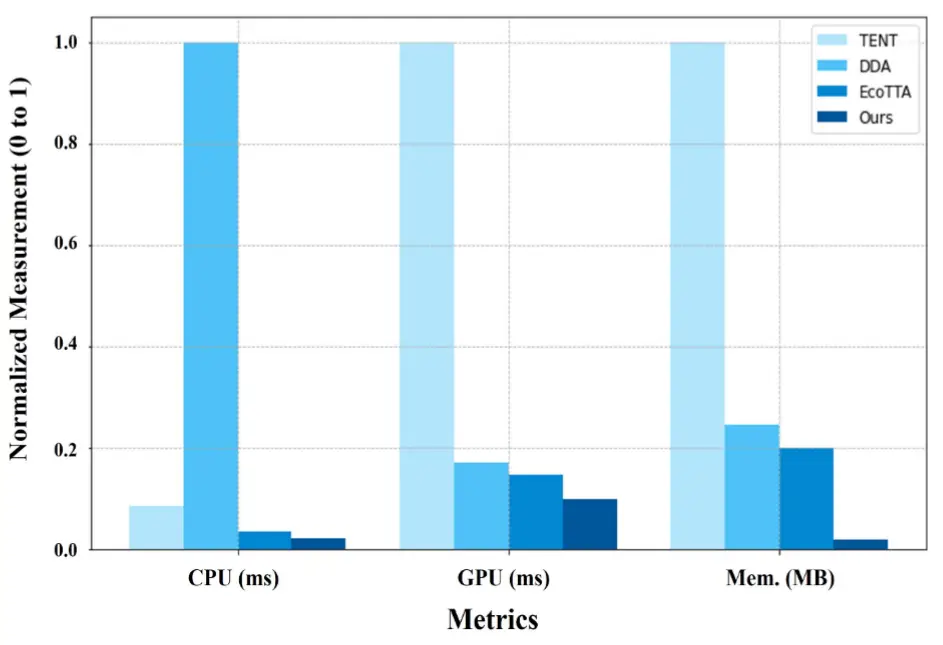
- 多种TTA方法在ResNet - 50上的训练时间对比
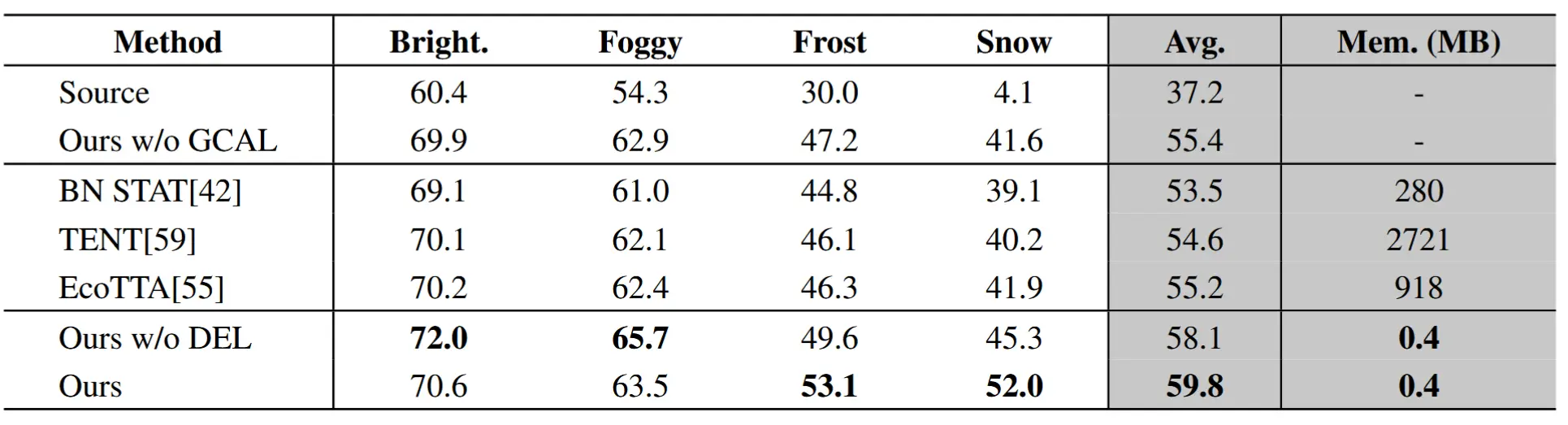
- 使用Deep LabV3Plus对Cityscapes - C进行语义分割的mIoU ( % )
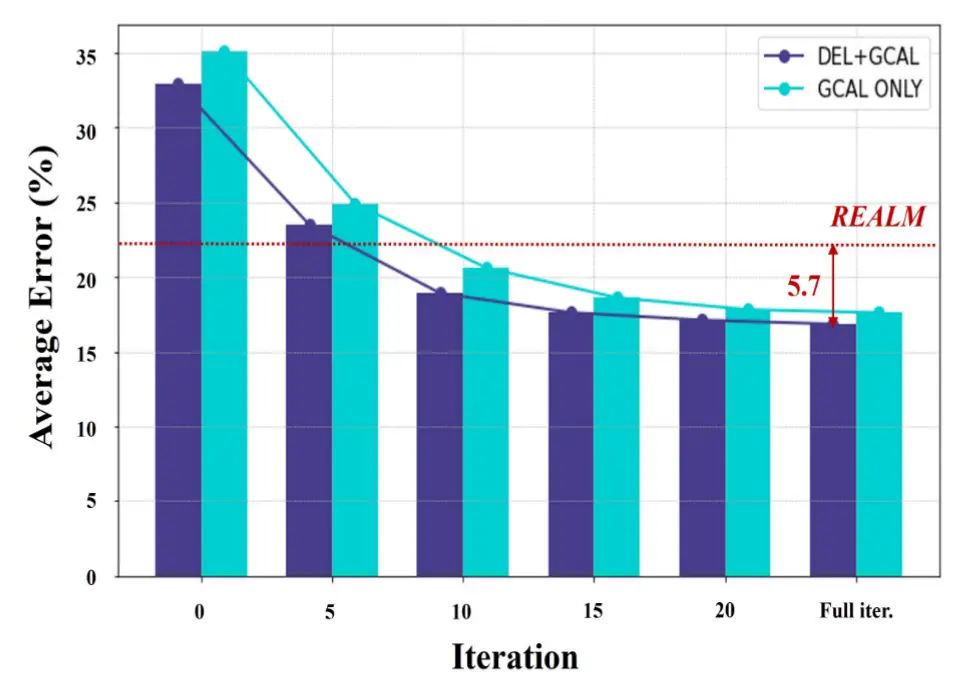
- 消融
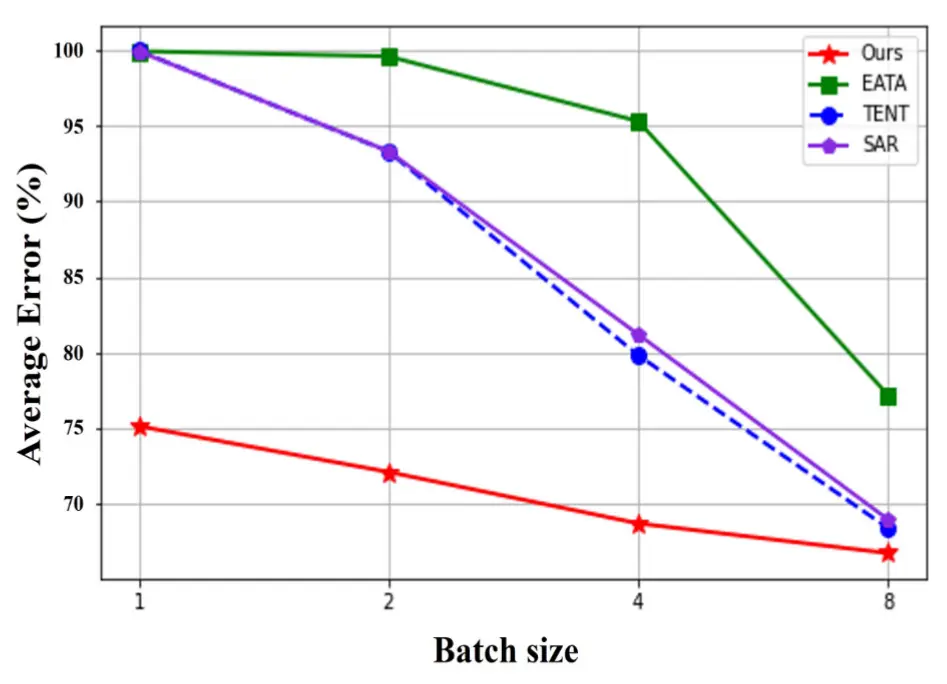
- 小batch size评估