论文笔记《TTA杂记》

论文笔记《TTA杂记》

Administrator 63 2025-04-09

一、SURGEON

  • 论文：《SURGEON: Memory-Adaptive Fully Test-Time Adaptation via Dynamic Activation Sparsity》
  • 关键词：开源、图像分类、语义分割、动态剪枝激活、CVPR2025

摘要：资源受限终端阻碍了大多数基于反向传播的TTA，因此本文为了解决内存限制问题，提出了SURGEON方法，一种新颖的 动态激活稀疏 策略，在适应过程中 以逐层动态比例直接修剪激活值 ，从而以数据敏感的方式灵活控制学习能力和内存消耗。在此过程中，梯度重要性和层激活内存 这两个指标被用来确定逐层修剪比例，分别反映精度贡献和内存效率。

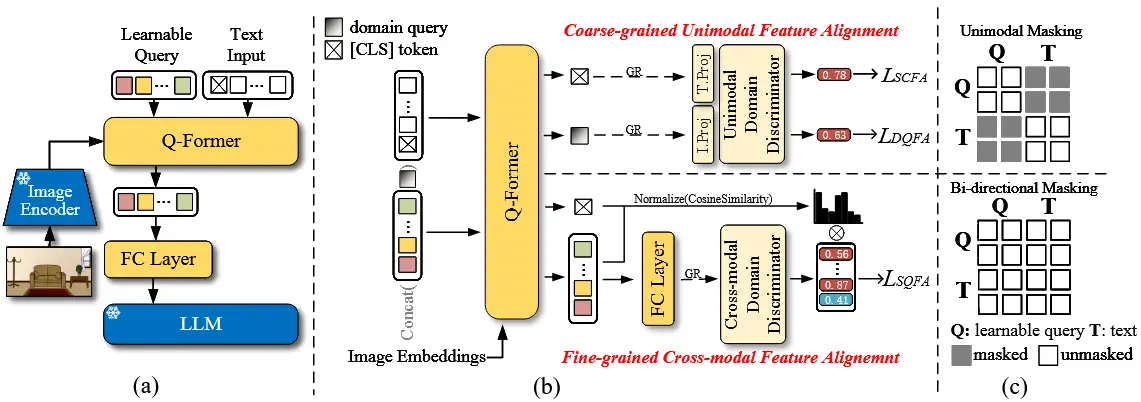
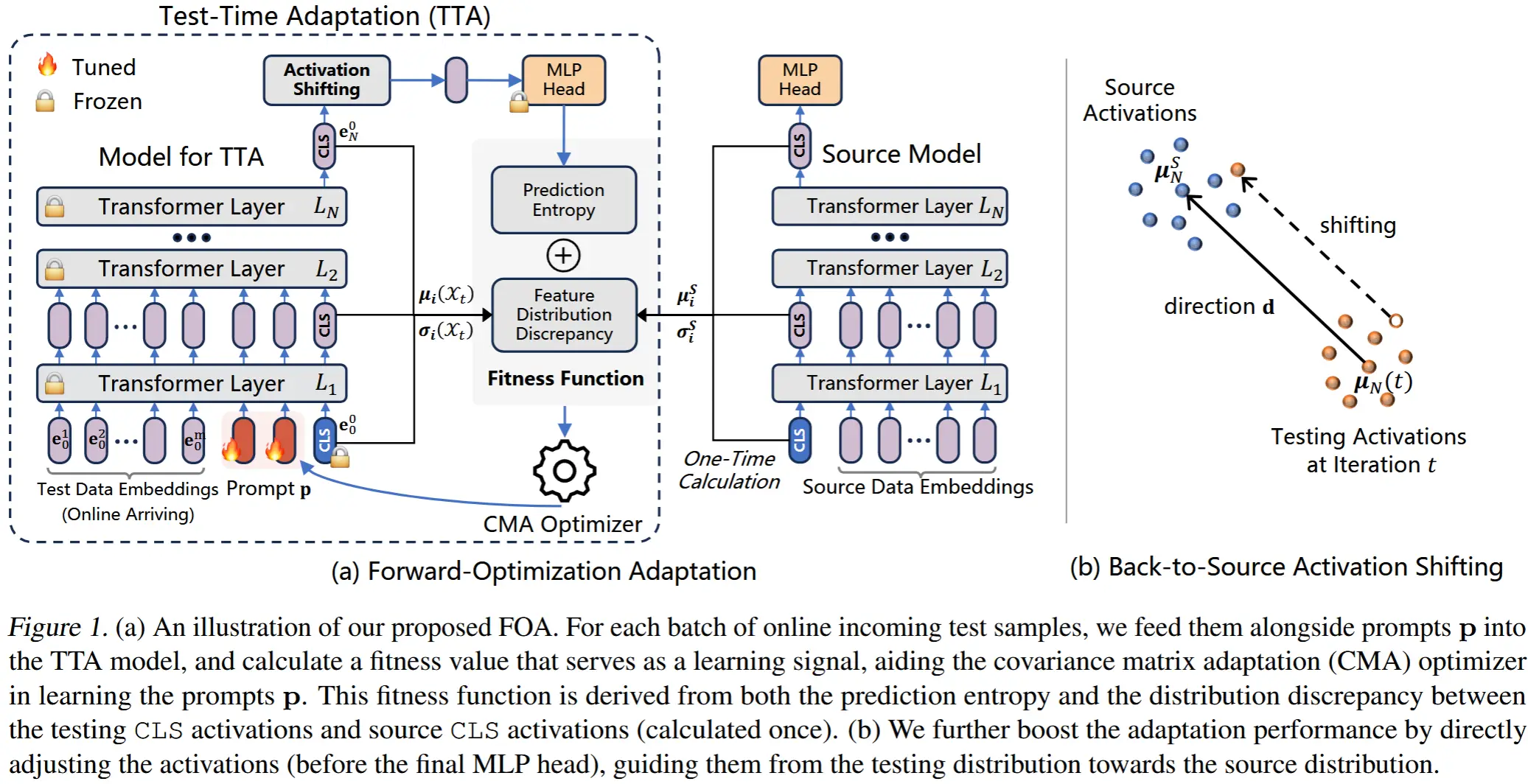
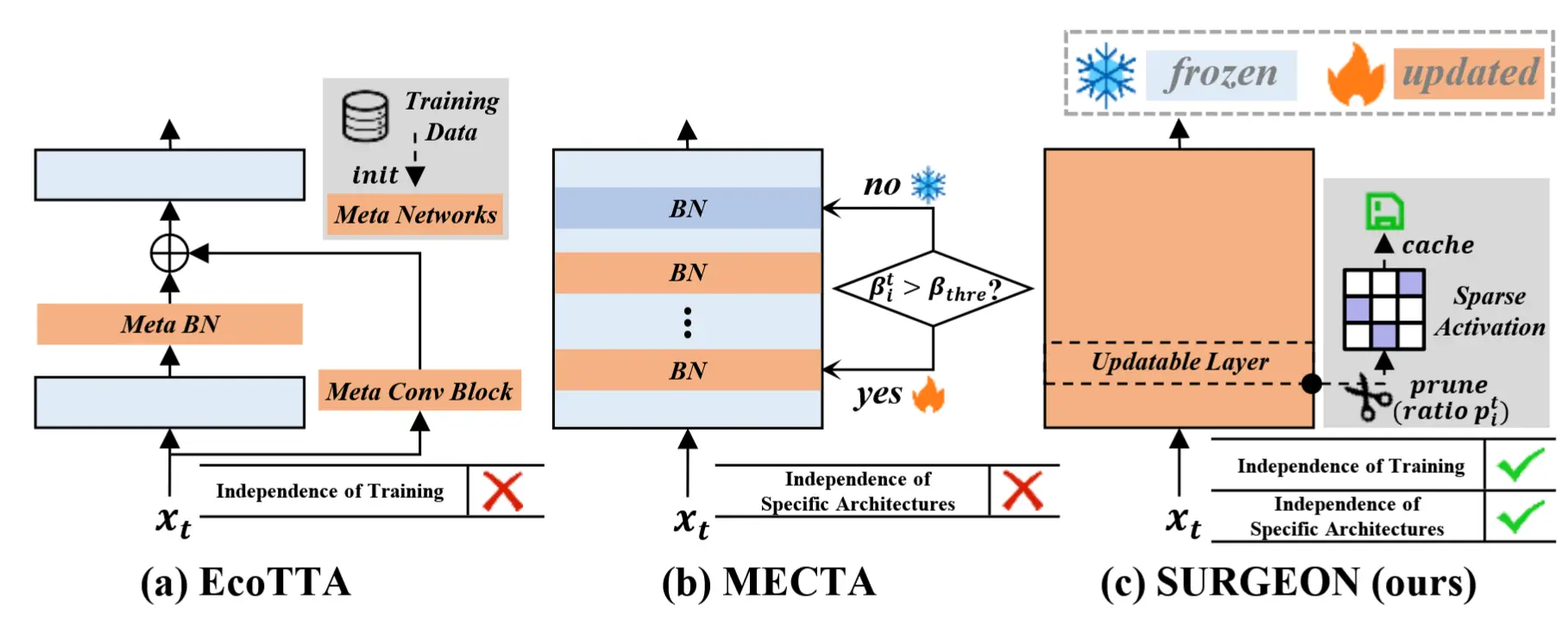
比较接近的工作局限性：（1）EcoTTA，它通过更新插件元网络来提高内存效率，同时保持主干冻结。但是，它需要在部署之前使用训练数据重新训练元网络几个 epoch，因此对于 FTTA 场景来说是不切实际的。（2）MECTA，通过优化批量大小、通道和适应层来减少内存使用，而无需修改原始训练程序。具体来说，它利用 BN 图层的统计数据来确定要更新的图层子集。然而，MECTA 对特定层的依赖限制了它对基于 transformer 的架构的适用性 [29]，这些架构通常缺乏 BN 层。

paper29-1.webp

梯度重要性

paper29-2.webp

使用 权重梯度 量化不同层的准确率贡献，因为具有较大梯度的层对模型预测和减少损失的影响更显着，这表明它们有可能捕获更丰富的知识并在当前数据上实现更高的准确性增益。

公式化为：

\Delta w_i = \frac{\partial L}{\partial w_i}, \quad G_i = \sqrt{\frac{\sum_{j=1}^{N_i} (\Delta w_j)^2}{N_i}}, \tag{4}

其中 ​\Delta w_j 是指第 i 层中神经元 j 的权重梯度，​N_i 表示神经元的数量。


层激活内存重要性

通过 激活 ​A_i 的大小来量化激活记忆效率，此指标直接反映更新层权重 Wi 所需的激活内存使用情况。

公式化：

m_i = size(A_i), M_i = -\log (\frac{m_i}{\sum^l_{i=1}m_i}), \tag{5}

其中 ​m_i 表示激活大小 ​A_i，而 ​M_i 是使用 ​m_i 与所有层的总激活大小之比的对数计算的。


重要度组合

I_i = Norm(M_i) × Norm(G_i), \tag{6}

其中 ​M_i 和 ​G_i 使用 Max Normalization 缩放为 [0,1] 以实现均匀性。


修剪比率

方程 （7） 说明了在当前数据批次 t 中将 ​I_i 转换为逐层修剪比率的过程：

p^t_i = 1 - \frac{I^t_i}{max_{i \in \{ 1,2,...,l\}} (I^t_i)}, \tag{7}

注意是​i \in \{ 1,2,...,l\}，因此在前向传播中逐层进行剪枝。


paper29-3.webp

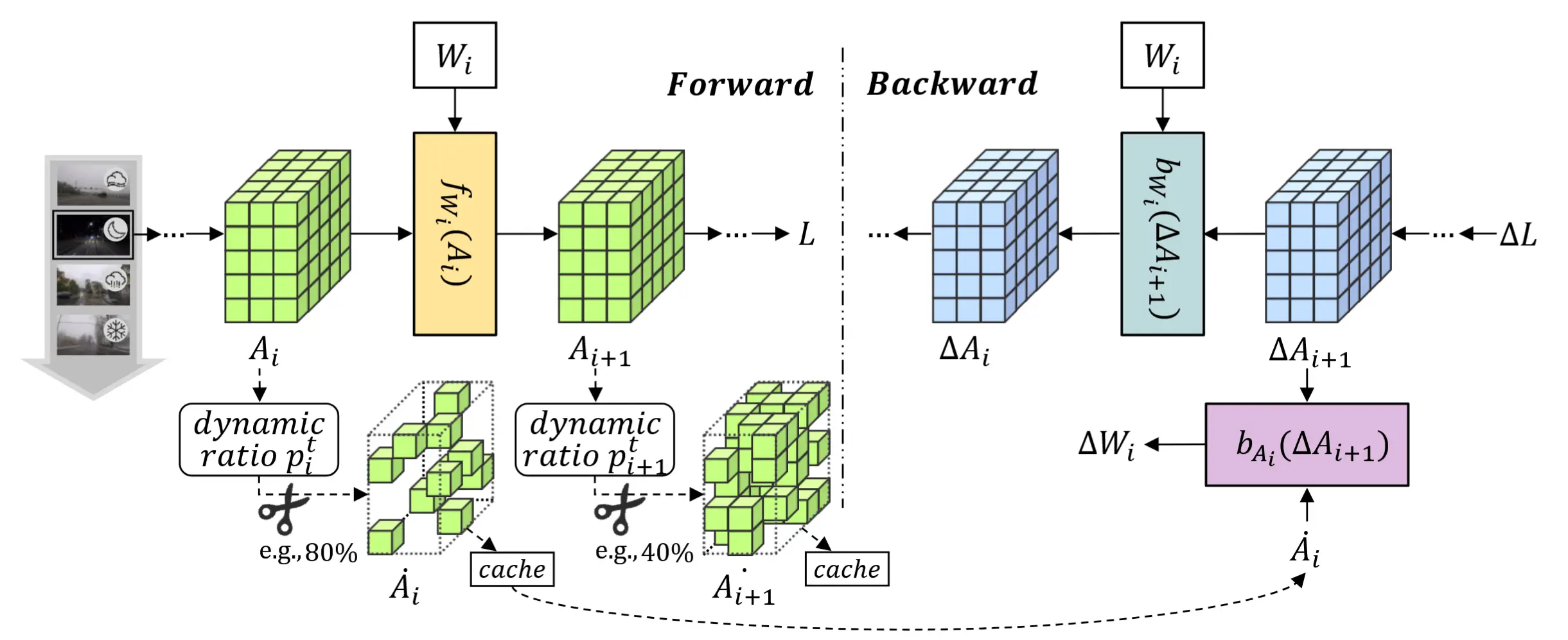
最初需要 一个额外的向前-向后过程 来计算重要性指标。为了降低额外进程的内存成本，并确保其不超过以下适配过程的峰值内存使用量，我们可以使用两种有效的策略：（i） 随机采样当前数据批次的一小部分，以及 （ii） 对活动应用高全局静态修剪率（例如，90%）。


二、EATA

  • 论文 - 《Efficient Test-Time Model Adaptation without Forgetting》
  • 关键词 - 开源、ICML2022、图像分类

摘要：现有方法问题：1）现有方法对每个测试样本都必须反向计算，导致成本过高。2）TTA后，在分布内数据上出现严重的性能下降（灾难性遗忘）。提出了一种 主动样本选择 准则，用于识别可靠且非冗余的样本，并在这些样本上更新模型以 最小化熵损失，从而实现测试时间自适应。此外，为了缓解遗忘问题，我们引入了一个 Fisher 正则化项，以约束重要模型参数避免剧烈变化，其中 Fisher 重要性通过带有生成伪标签的测试样本进行估计。

如图 1 所示，EATA 由两种策略组成。1） 样本高效熵最小化 旨在依靠主动样本选择策略进行有效适应。2） 防遗忘权重正则化，旨在通过强制对 ID 域很重要的参数在测试时适应中不会发生太大变化来减轻知识遗忘。

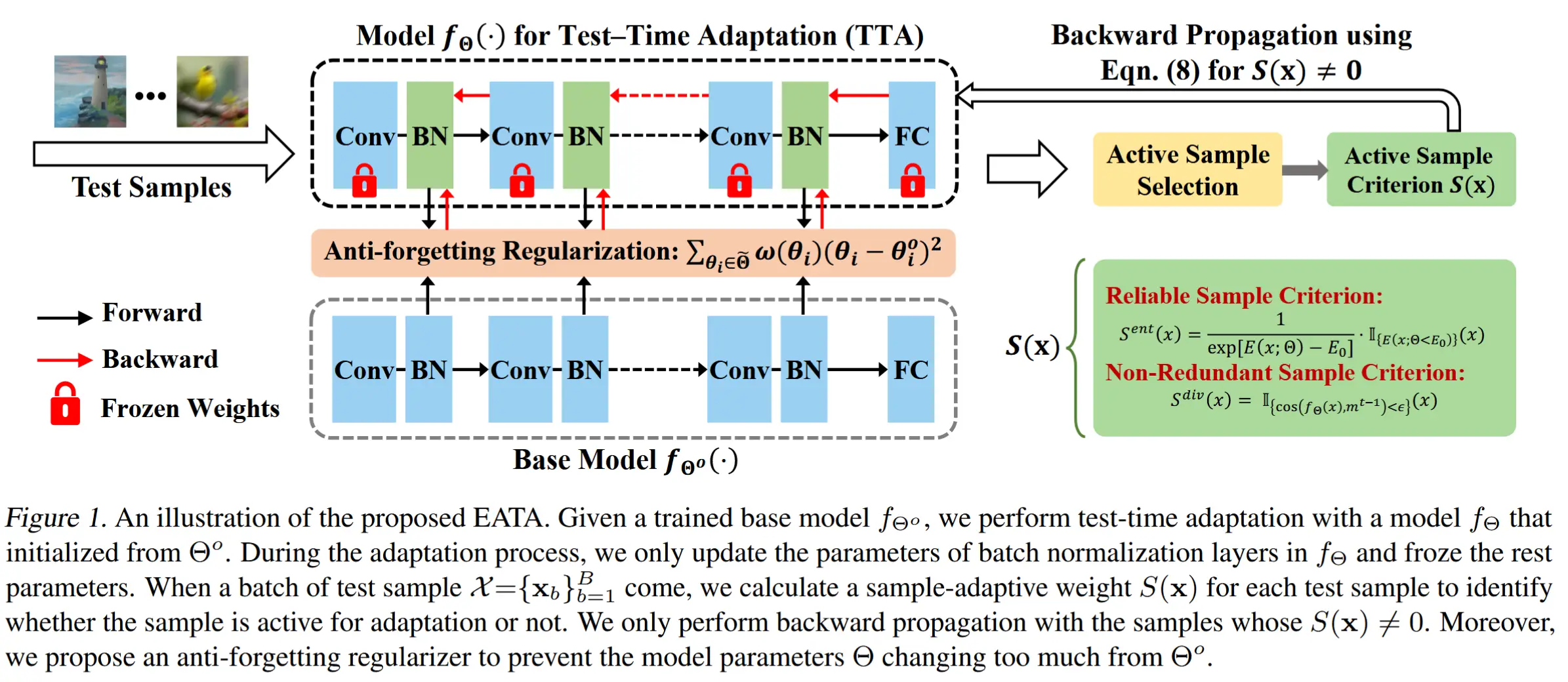
paper29-4.webp

样本高效熵最小化

作者根据两个标准为每个样本设计了一个主动样本选择分数S（x）：1） 样本对于测试时适应应该是可靠的；2） 优化中涉及的样本应该是非冗余的。

更新参数：batch normalization层的affine参数。

可靠样本的识别：作者通过实验，结果如图2，可以看出低熵样本更适合适应，而高熵样本会损害适应性能。

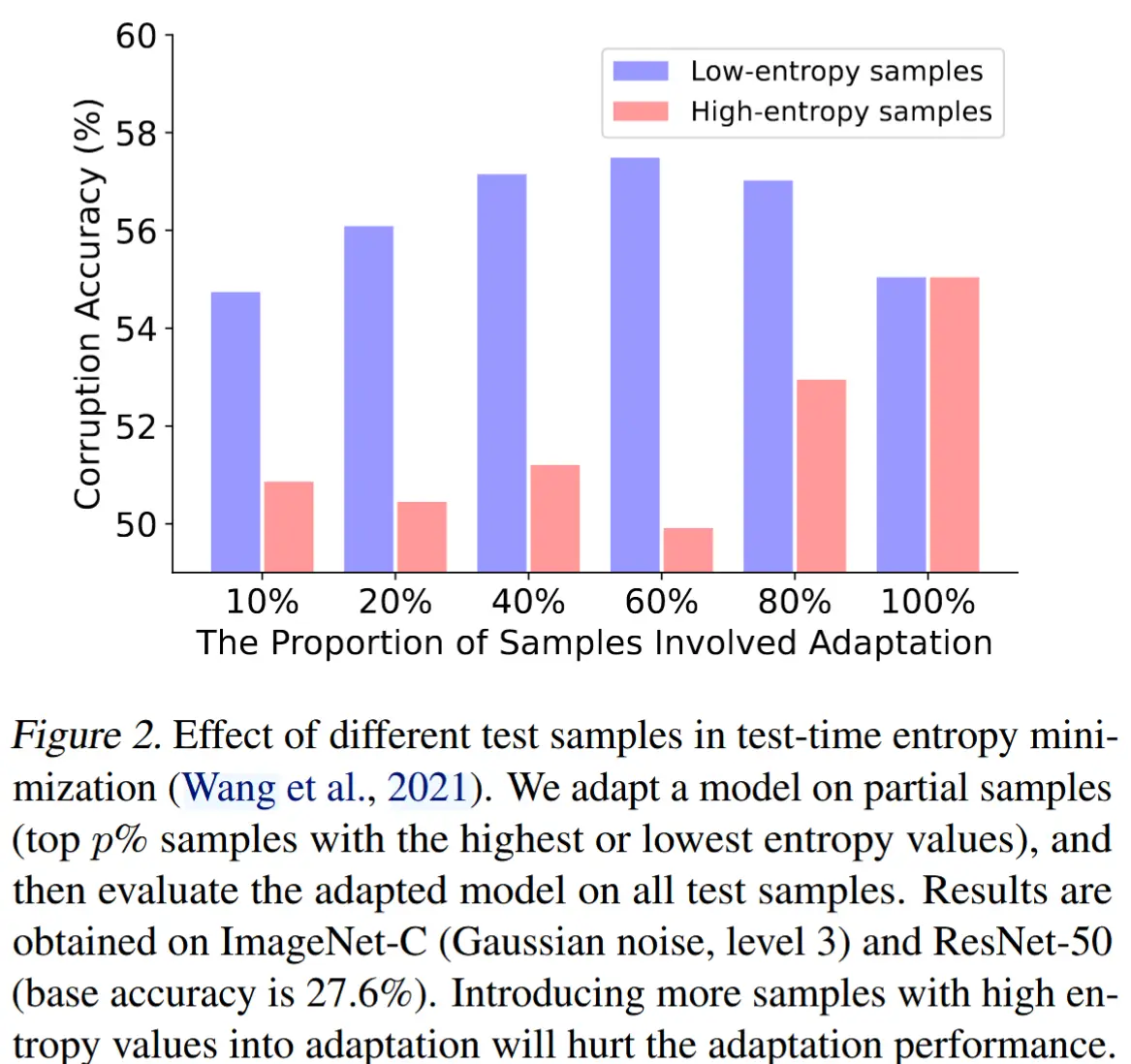
paper29-5.webp

基于上述观察，作者提出了一种基于熵的加权方案来识别可靠的样本。形式上，基于熵的权重由下式给出：

S^{\text{sent}}(\mathbf{x}) = \frac{1}{\exp[E(\mathbf{x}; \Theta) - E_0]} \cdot \mathbb{I}_{\{E(\mathbf{x}; \Theta) < E_0\}}(\mathbf{x}), \tag{3}

其中，​ \mathbb{I}_{\{\cdot\}}(\cdot) 是一个指示函数，​E(\mathbf{x}; \Theta) 表示样本 ​ \mathbf{x} 的熵，而 ​E_0 是一个预定义的阈值。上述加权函数排除了高熵样本的自适应，并为预测不确定性较低的测试样本分配更高的权重，允许它们对模型更新做出更多贡献。需要注意的是，计算 ​ S^{\text{sent}}(\mathbf{x}) 不涉及任何梯度反向传播。


去除冗余样本

尽管公式3选出了可靠样本进行梯度计算，但是仍然存在冗余近似的样本导致重复的反向传播。一种原始的方法是记录每个样本的输出概率，对于相似输出概率的样本进行丢弃，但是这会带来内存消耗的线性增加。

因此，作者利用 指数移动平均技术 来跟踪用于模型适应的所有可见测试样本的平均模型输出。具体来说，给定一组测试样本的模型输出，移动平均向量递归更新：

\mathbf{m}^t = \begin{cases} \bar{\mathbf{y}}^1, & \text{if } t = 1 \\ \alpha \bar{\mathbf{y}}^t + (1 - \alpha) \mathbf{m}^{t-1}, & \text{if } t > 1 \end{cases}, \tag{4}

其中，​\bar{\mathbf{y}}^t = \frac{1}{n} \sum_{k=1}^n \hat{\mathbf{y}}_k^t 是第 ​ t 次迭代时对一个 mini-batch 中的 ​n 个测试样本的平均模型预测值，且 ​ \alpha \in [0, 1] 。接下来，对于在 ​ t > 1 时接收到的新测试样本 ​ \mathbf{x} ，我们计算其预测 ​f_\Theta(\mathbf{x}) 与移动平均值 ​ \mathbf{m}^{t-1} （即 ​ \cos(f_\Theta(\mathbf{x}), \mathbf{m}^{t-1}) ）之间的 余弦相似度，然后使用该相似度确定基于多样性的权重：

S^{\text{div}}(\mathbf{x}) = \mathbb{I}_{\{\cos(f_\Theta(\mathbf{x}), \mathbf{m}^{t-1}) < \epsilon\}}(\mathbf{x}), \tag{5}

其中，​\epsilon 是预定义的余弦相似度阈值。整体样本自适应权重由以下公式给出：

S(\mathbf{x}) = S^{\text{ent}}(\mathbf{x}) \cdot S^{\text{div}}(\mathbf{x}), \tag{6}

这结合了基于熵的项（公式 (3) ）和基于多样性的项（公式 (5) ）。


Fisher 正则化

目的：缓解测试时间自适应（TTA）引起的灾难性遗忘问题，即测试时间自适应后的模型性能可能在分布内（ID）测试样本上显著下降。

我们通过权重正则化实现这一目标，该正则化仅影响损失函数，且不会为模型自适应引入额外的计算开销。具体来说，我们应用一种感知重要性的正则化器 ​ \mathcal{R} ，以防止对分布内域重要的模型参数在测试时间自适应过程中发生过多变化：

\mathcal{R}(\tilde{\Theta}, \tilde{\Theta}^o) = \sum_{\theta_i \in \tilde{\Theta}} \omega(\theta_i) (\theta_i - \theta_i^o)^2, \tag{7}

其中，​\tilde{\Theta} 是用于模型更新的参数，而 ​ \tilde{\Theta}^o 是原始模型的对应参数。​\omega(\theta_i) 表示参数 ​ \theta_i 的重要性，我们通过 对角 Fisher 信息矩阵 来衡量其重要性。在这里，Fisher 信息 ​ \omega(\theta_i) 的计算并不简单，因为我们无法访问任何带标签的训练数据。为了便于展示，我们在下一小节中详细说明 ​ \omega(\theta_i) 的计算细节。

引入防遗忘正则化器后，我们的方法的最终优化公式可以表示为：

\min_{\tilde{\Theta}} S(\mathbf{x}) E(\mathbf{x}; \Theta) + \beta \mathcal{R}(\tilde{\Theta}, \tilde{\Theta}^o), \tag{8}

其中，​\beta 是权衡参数，​S(\mathbf{x}) 和 ​ E(\mathbf{x}; \Theta) 在公式 (2) 中定义。


权重重要性 ​\omega(\theta_i) 的测量

Fisher 信息的计算通常需要一组带标签的分布内（ID）训练样本。然而，在我们的问题设置中，我们无法访问训练数据，且测试样本是无标签的，这使得衡量权重的重要性变得困难。为了解决这一问题，我们首先收集一小部分无标签的分布内测试样本 ​ \{\mathbf{x}_q\}_{q=1}^Q ，然后使用原始训练好的模型 ​ f_\Theta(\cdot) 对这些样本进行预测，以获得相应的 硬伪标签 ​ \hat{y}_q 。接下来，基于这些样本 构建伪标签分布内测试集 ​ D_F = \{\mathbf{x}_q, \hat{y}_q\}_{q=1}^Q ，并通过以下公式计算模型权重的 Fisher 重要性：

\omega(\theta_i) = \frac{1}{Q} \sum_{\mathbf{x}_q \in D_F} \left( \frac{\partial \mathcal{L}_{CE}(f_{\Theta^o}(\mathbf{x}_q), \hat{y}_q)}{\partial \theta_i^o} \right)^2, \tag{9}

其中，​ \mathcal{L}_{CE} 是交叉熵损失。在这里，我们只需在执行测试时间自适应之前计算一次 ​\omega(\theta_i) ，一旦计算完成，就将其固定并应用于任何类型的分布偏移。此外，无标签的分布内测试样本是基于分布外检测技术收集的，这些技术易于实现。需要注意的是，无需收集过多的分布内测试样本来计算 ​ \omega(\theta_i) 。


三、DPAL

  • 论文 - 《Dual-Path Adversarial Lifting for Domain Shift Correction in Online Test-time Adaptation》
  • 关键词 - 开源、TTA、Transformer-base、图像分类、Prompt

摘要：本文重点关注为 Transformer 模型设计高效的测试时间自适应方法。在本工作中，作者受到多尺度信号处理中 双子带小波提升方案（dual-subband wavelet lifting scheme） 的启发，该方案能够高效地 将输入信号分离为主成分和噪声成分，因此我们引入了一种用于测试时间自适应中的 域偏移校正的双路径 token 提升 方法。具体而言，我们在 Transformer 网络的每一层引入了一个额外的 token，称为 域偏移 token。然后，我们在 域偏移 token 路径 和 类别 token 路径 之间执行双路径提升，并在网络的所有层中进行交错的 token 预测与更新。预测和更新网络以对抗的方式进行学习。具体来说，预测网络的任务是学习域偏移的残差噪声，这种噪声在目标域中的所有类别和所有样本之间应具有较大的不变性。另一方面，更新网络的任务是通过从输入图像样本中移除域偏移来更新类别 token，从而使输入样本在特征空间中对不同类别更具区分性。为了有效学习具有两个对抗任务的预测和更新网络，我们从理论和实践上证明了，对于更新网络需要使用平滑优化，而对于预测网络则需要使用非平滑优化。


动机：如图 1 ，作者观察到域偏移对 Transformer 网络中的自注意力图有显著影响，如何从被域偏移破坏的自注意力图中去除噪声是将TTA适配到 Transformer 的核心挑战。

paper29-6.webp

方法概述

信号处理中的提升方案包含三个步骤：分割、预测和更新。在分割步骤中，信号被分为两个独立的信号。随后，预测步骤旨在消除初始分割后的噪声。接着，更新步骤通过去除这些噪声来校正信号。经过这三个步骤后，输入信号被分离为主成分和噪声成分。

在本工作中，我们为在线测试时间自适应中的域偏移校正引入了一种双路径 token 提升方法。当对具有 ​L 层和 token 维度 ​ d 的基于 Transformer 的模型进行高效适配时（如图 2 所示），我们在 Vision Transformer (ViT) 的每一层类别 token ​ \mathbf{C} = \{C_1, C_2, \cdots, C_L\} 前引入了一个额外的域偏移 token ​\mathbf{P} = \{P_1, P_2, \cdots, P_L\} 。随后，我们引入一个提升块，包括轻量级 MLP 预测网络 ​ \boldsymbol{\Phi} = \{\Phi_1, \Phi_2, \cdots, \Phi_L\} 和 更新网络 ​\boldsymbol{\Psi} = \{\Psi_1, \Psi_2, \cdots, \Psi_L\} 。预测网络的目标是预测第 ​ l 层的域偏移特征 ​\pi_l 。利用域偏移特征，我们使用更新网络从原始类别 token 特征中去除域偏移特征，计算最终特征。假设 Transformer 编码器在第 ​l 层将图像特征分为两个输出：域偏移 token 输出 ​f_l^d 和类别 token 输出 ​f_l^c 。预测网络 ​\Phi_l 进行域偏移预测，表示为 ​ \pi_l = \Phi_l(f_l^d) 。随后，更新网络 ​\Psi_l 对下一层的类别 token 进行更新，表示为 ​C_{l+1} = \Psi_l(f_l^c, \pi_l) 。

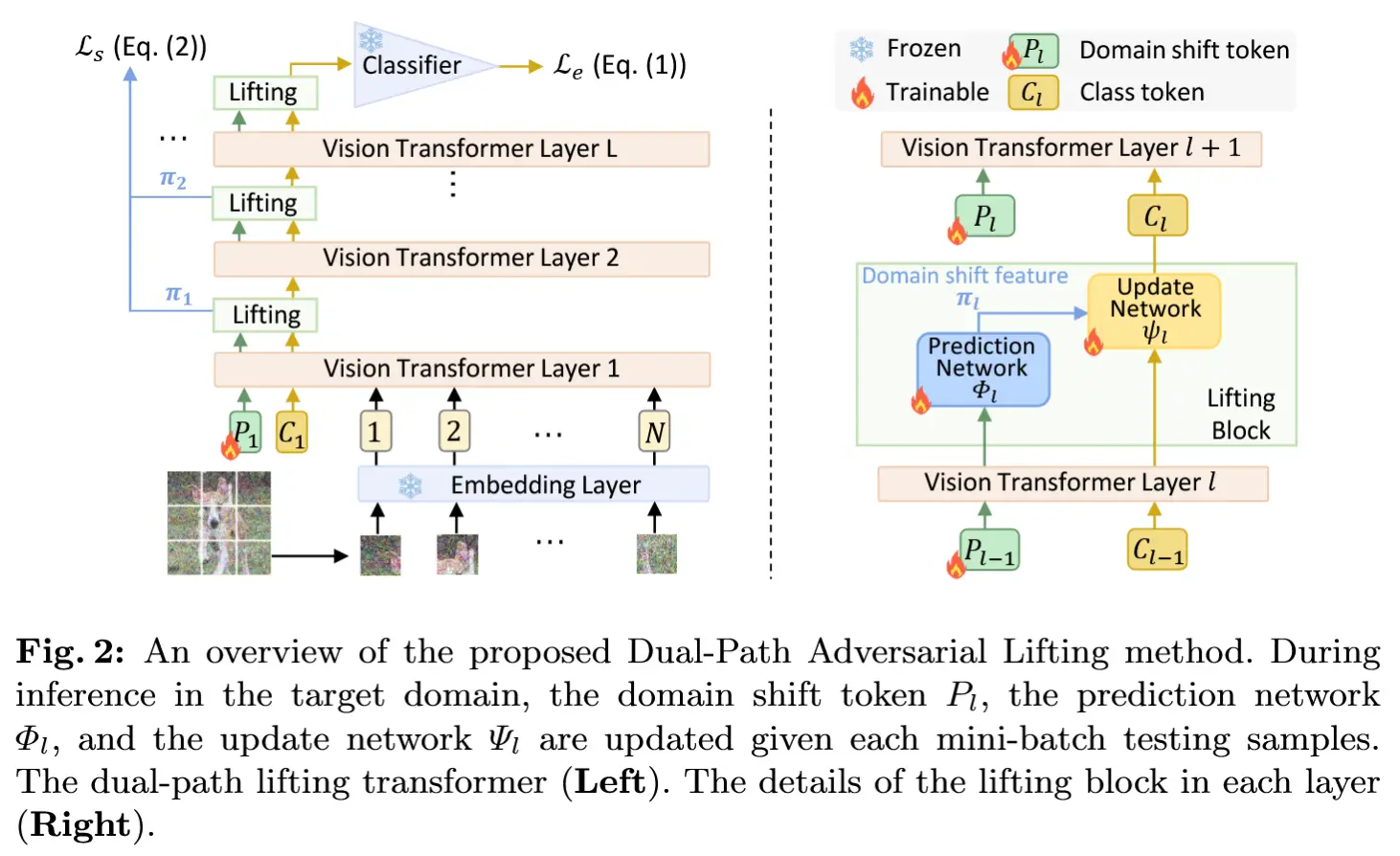
paper29-7.webp

双路径 Token 提升用于域偏移校正

我们引入了两个损失函数来指导在线自适应过程，分别称为可靠熵损失 ​ \mathcal{L}_e(\theta_t; x) 和 相似性损失 ​ \mathcal{L}_s(\theta_t; x) 。

在测试过程中，对于当前小批量 ​\mathbf{B}_t 中的样本 ​ x ，可靠熵损失定义为：

\mathcal{L}_e(\theta_t; x) = \mathbf{I} \cdot \mathbb{E}(\theta_t; x), \tag{1}

其中，​ \mathbf{I} = \mathbb{I}[\mathbb{E}(\theta_t; x) < E_0] 是一个掩码，用于过滤掉熵大于阈值 ​ E_0 的测试样本，​ \mathbb{E} 是熵函数。

对于具有 ​L 层的 ViT 模型，相似性损失定义为：

\mathcal{L}_s(\theta_t; x) = -\frac{1}{L} \sum_{l=1}^L \frac{1}{B^2} \sum_{j=1}^B \sum_{k=1}^B M_l^{jk}, \tag{2}

其中，​ B 表示批次大小，​ M 是从预测网络中获得的每对域偏移特征 ​\pi_l 计算出的 余弦相似性矩阵，且 ​\pi_l \in \mathcal{R}^{B \times d} 。

在熵损失 ​\mathcal{L}_e(\theta_t; x) 的基础上，结合相似性损失 ​ \mathcal{L}_s(\theta_t; x) 以鼓励预测网络学习特定于域的信息，从而得到以下损失函数：

\mathcal{L}(\theta_t; x) = \mathcal{L}_e(\theta_t; x) + \lambda \cdot \mathcal{L}_s(\theta_t; x). \tag{3}

这里，​ \lambda = \frac{\sum \mathbf{I}}{B} 作为平衡参数，其中 ​ \sum \mathbf{I} 表示批次上的熵掩码之和。

预测网络和更新网络以对抗的方式进行学习。这是因为预测网络学习的是域偏移的残差噪声（学习不变的噪声），而更新网络通过从输入图像样本及其分块中移除域偏移来更新类别token（区分不同类别的样本）。受域对抗学习 [39] 的启发，为了有效学习具有两个对抗任务的预测网络和更新网络，作者对预测网络采用平滑优化，而对更新网络采用非平滑优化。


类别 Token 更新网络的平滑优化

我们采用 SAR 方法 [36] 来执行 Sharpness-Aware Minimization (SAM) [7] 对更新网络进行优化。从泛化和优化的角度来看，SAM 不仅最小化损失函数中的单个点，还一致地减少了其邻域内的损失。与传统方法仅针对低损失值优化模型权重不同，SAM 力图在权重空间中寻找更平滑的极小值。这些极小值的特点是，在模型权重 ​\theta 的邻域 ​\epsilon 中具有均匀较低的损失 ​\mathcal{L} ：

\min_{\theta} \max_{||\epsilon|| \leq \rho} \mathcal{L}(\theta + \epsilon; x), \tag{4}

其中，​\rho \geq 0 是定义邻域范围的超参数。为了解决这一极大极小问题，SAM 首先通过寻找训练步骤 ​ t 上的最大扰动 ​ \epsilon_t 来解决最大化问题。这个内层最大化问题可以通过对 ​ \mathcal{L}(\theta + \epsilon; x) 关于 ​\epsilon \to 0 的一阶泰勒展开近似表示如下：

\epsilon_t(\theta) = \arg\max_{||\epsilon|| \leq \rho} \mathcal{L}(\theta + \epsilon; x) \\ = \arg\max_{||\epsilon|| \leq \rho} \mathcal{L}(\theta; x) + \epsilon^\text{T} \nabla_\theta \mathcal{L}(\theta; x) + o(\epsilon) \\ \approx \arg\max_{||\epsilon|| \leq \rho} \epsilon^\text{T} \nabla_\theta \mathcal{L}(\theta; x). \tag{5}

求解该近似的值由经典对偶范数问题的解给出：

\epsilon_t(\theta) = \rho \cdot \text{sign}(\nabla_\theta \mathcal{L}(\theta; x)) \frac{|\nabla_\theta \mathcal{L}(\theta; x)|^{q-1}}{\|\nabla_\theta \mathcal{L}(\theta; x)\|_q^{q/p}}, \tag{6}

其中，​\frac{1}{p} + \frac{1}{q} = 1 。实验证明 ，当 ​ p = 2 时，优化效果最佳，从而得到 ​\epsilon_t 的公式为：

\epsilon_t(\theta) = \rho \frac{\nabla_\theta \mathcal{L}(\theta; x)}{\|\nabla_\theta \mathcal{L}(\theta; x)\|_2}. \tag{7}

然后，模型权重 ​ \theta_t 的梯度更新计算如下：

\theta_{t+1} = \theta_t - \eta \nabla_\theta \mathcal{L}(\theta; x)|_{\theta_t + \epsilon_t}. \tag{8}

最后，SAM 通过迭代更新公式 (7) 和公式 (8)，将模型权重 ​ \theta 收敛到损失函数 ​\mathcal{L} 的一个 平滑极小值。


偏移 Token 预测网络的非平滑优化

为什么预测未来用非平衡优化？

最近的文献 [39] 指出，收敛于对抗性损失收敛到平滑极小值会导致次优的泛化性能。受对抗学习中这种非平滑优化的启发，在我们的研究中，我们观察到，相对于相似性损失的非平滑极小值能够促使预测网络更好地学习域偏移信息，从而在目标域上实现更好的泛化性能。

我们通过预测网络 ​ \Phi 对特征的相似性估计来衡量域偏移预测，表示为 ​S_\Phi = \mathbb{E}[\sum M] 。相似度越高，表明在小批量样本中对域特定知识的提取越有效，这意味着对域偏移的估计更准确。目标是最大化相似性估计 ​ S_\Phi ，其中 ​ S_{\Phi^*} 表示最优相似度。

为了理论分析光滑版本 ​ S_{\Phi'} 和非光滑版本 ​S_{\Phi''} 之间的相似性估计差异，我们将 ​ S_\Phi 视为一个 ​ L-smooth 函数 [2]，其中 ​ \eta 表示一个小常数。在测试阶段的一次梯度更新步骤中，令 ​ \Phi' = \Phi + \eta \mathbf{v}_1 ，其中 ​ \mathbf{v}_1 = (\nabla S_\Phi / ||\nabla S_\Phi||) ，并且 ​\Phi'' = \Phi + \eta \mathbf{v}_2 ，其中 ​\mathbf{v}_2 = (\nabla S_\Phi|_{\Phi+\epsilon_t(\Phi)} / ||\nabla S_\Phi|_{\Phi+\epsilon_t(\Phi)}||) 。

在线自适应过程中，在测试阶段仅使用一步梯度进行相似性估计时，对于小的 ​ \eta 和梯度方向 ​ \mathbf{v}_1 ，任何微分函数都可以用线性近似表示：

S_{\Phi + \eta \mathbf{v}_1} \approx S_\Phi + \eta \mathbf{v}_1 \cdot \nabla S_\Phi. \tag{9}

将两个向量之间的点积表示为范数和它们之间的夹角 ​\alpha ：

\mathbf{v}_1 \cdot \nabla S_\Phi = ||\nabla S_\Phi|| \, ||\mathbf{v}_1|| \, \cos \alpha, \tag{10}

当 ​ \cos \alpha = 1 时，我们达到最大值，这表明 ​ \mathbf{v}_1 = \frac{\nabla S_\Phi}{||\nabla S_\Phi||} 。

现在，将另一个方向上的梯度下降 ​ \mathbf{v}_2 = \frac{\nabla S_\Phi|_{\Phi+\epsilon_t(\Phi)}}{||\nabla S_\Phi|_{\Phi+\epsilon_t(\Phi)}||} 与光滑优化进行比较，其差异可以由以下公式表征：

S_{\Phi + \eta \mathbf{v}_1} - S_{\Phi + \eta \mathbf{v}_2} = \eta ||\nabla S_\Phi|| (1 - \cos \beta), \tag{11}

其中 ​ \beta 是 ​ \mathbf{v}_1 : \nabla S_\Phi|_{\Phi} 和 ​ \mathbf{v}_2 : \nabla S_\Phi|_{\Phi+\epsilon_t(\Phi)} 之间的角度。次优性依赖于梯度的幅度。利用以下结果，我们证明了当最优性差距 ​S_{\Phi^*} - S_\Phi 较大时，这两个方向之间的差异也较大。对于一个 ​L-smooth，该函数既连续可微，又具有 Lipschitz 连续梯度，其 Lipschitz 常数记为 ​L，我们基于 [39] 推导出以下不等式方程：

\left( \frac{S_{\Phi + \eta \mathbf{v}_2} - S_{\Phi + \eta \mathbf{v}_1}}{\eta (1 - \cos \beta)} \right)^2 \leq 2L(S_{\Phi^*} - S_\Phi), \tag{13}
(S_{\Phi'} - S_{\Phi''})^2 \leq 2L\eta^2 (1 - \cos \beta)^2 (S_{\Phi^*} - S_\Phi). \tag{14}

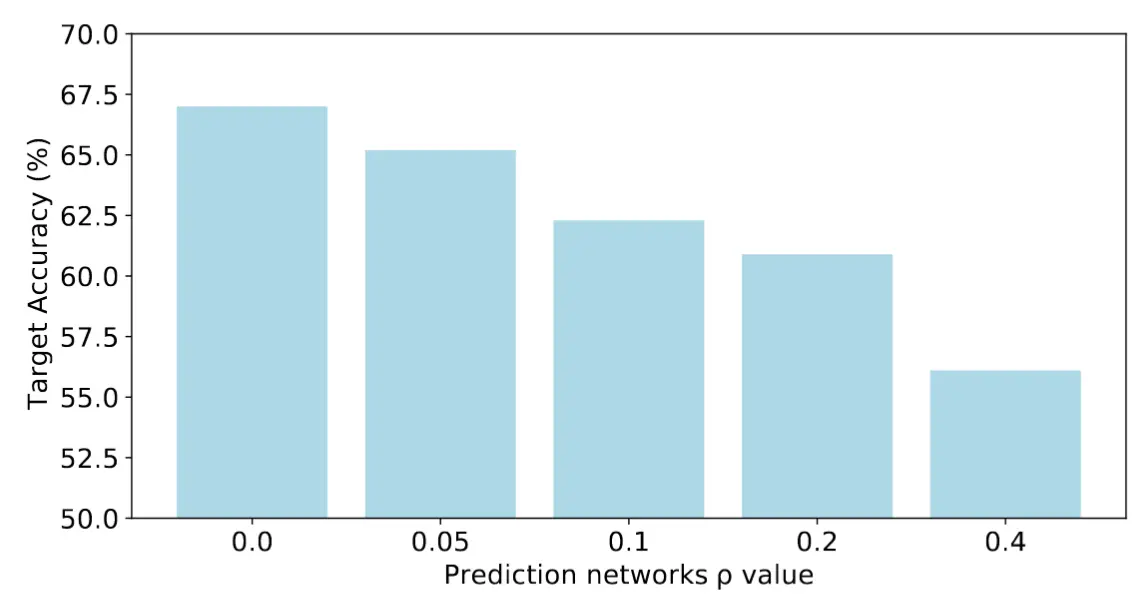
公式 (14) 表明，在梯度方向 ​\mathbf{v}_1 和另一个方向 ​ \mathbf{v}_2 上的值之间的差异被 ​ S_{\Phi^*} - S_\Phi 上界约束。因此，如果距离最优值较远，这种差异可能会很大。在在线测试时间自适应过程中，仅进行一步梯度更新时，其中 ​ S_{\Phi^*} - S_\Phi 可能较大，光滑版本 ​S_{\Phi'} 可能会远离正常的非平滑梯度更新相似性估计，导致次优的相似性度量。在我们的实验中，如图 3 所示，我们还观察到，相对于相似性损失增加预测网络的平滑度（即增加邻域范围的尺度值 ​ \rho ）会导致目标域上的性能下降。这是因为在预测网络中，随着相似性损失的平滑度增加，预测网络倾向于学习更多语义知识而非特定于域的知识。这可能会导致在后续的更新网络中丢失关键的语义信息。由于公式 (14) 中差异的上界变大，这种语义信息的丢失可能对分类精度有害。因此，从理论和实践上来看，预测网络的非平滑优化表现更好。

paper29-8.webp

四、2LTTA

  • 论文 - 《Two-Level Test-Time Adaptation in Multimodal Learning》
  • 关键词 - ICML2024、多模态TTA

摘要：在多模态任务中，由单模态数据损坏引起的可靠性偏差尚未得到充分讨论。虽然一些最新的方法通过调节模态共享模块来抑制跨模态信息差异（即可靠性偏差），但针对模态特定模块的域自适应却被忽视了。在本文中，作者提出了一种 两级测试时间自适应方法（称为 2LTTA ），该方法同时考虑了多模态学习中的 模态内分布偏移 和 跨模态可靠性偏差 。2LTTA 调节与受损模态对应的 编码器 的所有 归一化层和自注意力模块，以及 模态共享块。此外，本文采用了一个 两级目标函数，在模态融合块中同时考虑模态内分布偏移和跨模态可靠性偏差。利用带样本重加权的香农熵来减少数据损坏引起的模态内分布偏移，并采用一种促进多样性的损失函数来减少跨模态信息差异。


两级目标函数

（目标一：香农熵）

在 intra-modality level 引入基于 Transformer 编码器输出嵌入的 香农熵 ​ E_{\text{ent}}(x; \widetilde{\Theta}) 作为目标函数。其定义如下：

E_{\text{ent}}(x; \widetilde{\Theta}) = -\frac{1}{B} \sum_{i=1}^B \sum_{\tilde{y} \in \tilde{\mathcal{C}}} p(\tilde{y}|x_i; \widetilde{\Theta}) \log p(\tilde{y}|x_i; \widetilde{\Theta}), \tag{1}

其中，​p(\tilde{y}|x_i; \widetilde{\Theta}) 表示 受损模态 Transformer 编码器输出嵌入的 softmax 值，而 ​ \tilde{\mathcal{C}} 是对应的输出空间（即输出嵌入中的元素数量）。​ B 是小批量的大小。

通过预定义的加权函数对小批量的熵损失进行重新加权。Transformer 编码器在模态内层适应的优化目标可以表示为：

\min_{\widetilde{\Theta}_i, i \in \hat{S}} S_{\text{ent}}(x) E_{\text{ent}}(x; \widetilde{\Theta}), \tag{2}

其中，​ S_{\text{ent}} 是 加权函数，定义为：

S_{\text{ent}}(x) = \frac{1}{\exp\left(E_{\text{ent}}(x; \widetilde{\Theta}) - 0.4 \cdot E_{\max}\right)}, \tag{3}

且 ​ E_{\max} = \ln \tilde{\mathcal{C}} 。


（目标二：促进多样化）

在 cross-modality level，作者引入一种 促进多样性 的损失来减少由模态损坏引起的信息差异的影响。香农熵旨在鼓励调整后的模型生成接近 one-hot 编码的判别性输出。然而，在实践中，理想的输出应类似于 one-hot 编码，但彼此之间存在差异（即样本间具有多样性）。为此，我们向目标函数中添加一个 正则化项 ，以考虑数据样本间的多样性，具体如下：

E_{\text{div}}(x; \Theta) = \sum_{y \in \mathcal{C}} \hat{p}_y \log \hat{p}_y, \tag{4}

其中，​\hat{p}_y 是每个大小为 ​ B 的 小批量中所有测试样本的 softmax 输出的平均值，​ C 是融合块的输出空间（即类别集合）。​E_{\text{div}} 被称为促进多样性目标函数。


参数更新策略

可学习参数：受损模态的 Transformer 编码器中的 浅层注意力模块和 LN 层、融合层、投影层、以及融合块中所有 LN 层。

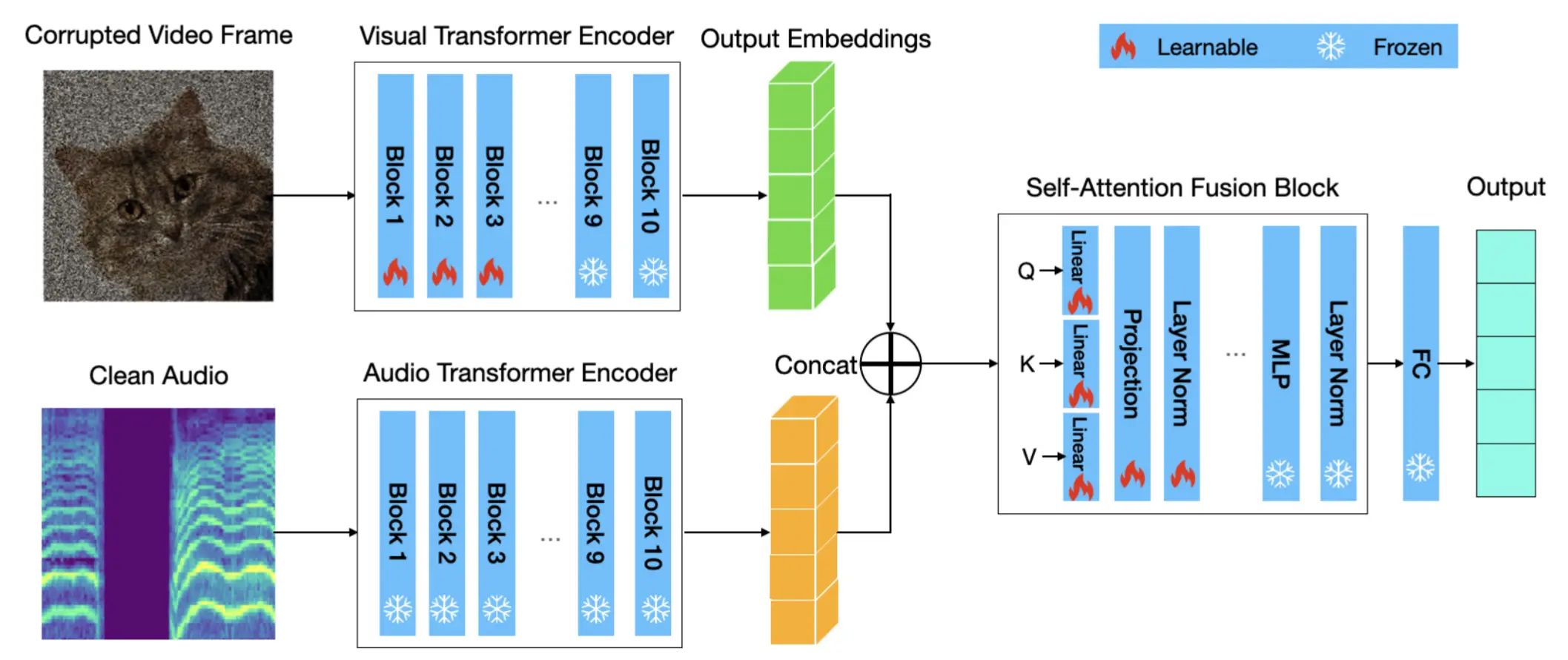
paper29-9.webp

与 Lee 等人（2022）类似，我们仅针对网络中的一部分子集的参数进行优化。

两级 TTA（2LTTA）的目标函数可以表示为：

\min_{\Theta_i, i \in \hat{S}; \tilde{\Theta}_j, j \in \tilde{S}} S_{\text{ent}}(x) E_{\text{ent}}(x; \widetilde{\Theta}) + \alpha E_{\text{div}}(x; \Theta), \tag{6}

其中，​ \alpha > 0 是促进多样性的超参数。具体来说，​ \hat{S} 表示整个网络中可训练参数的子集，而 ​ \tilde{S} 仅表示受损模态的 Transformer 编码器中可训练参数的子集。

TTA 论文笔记