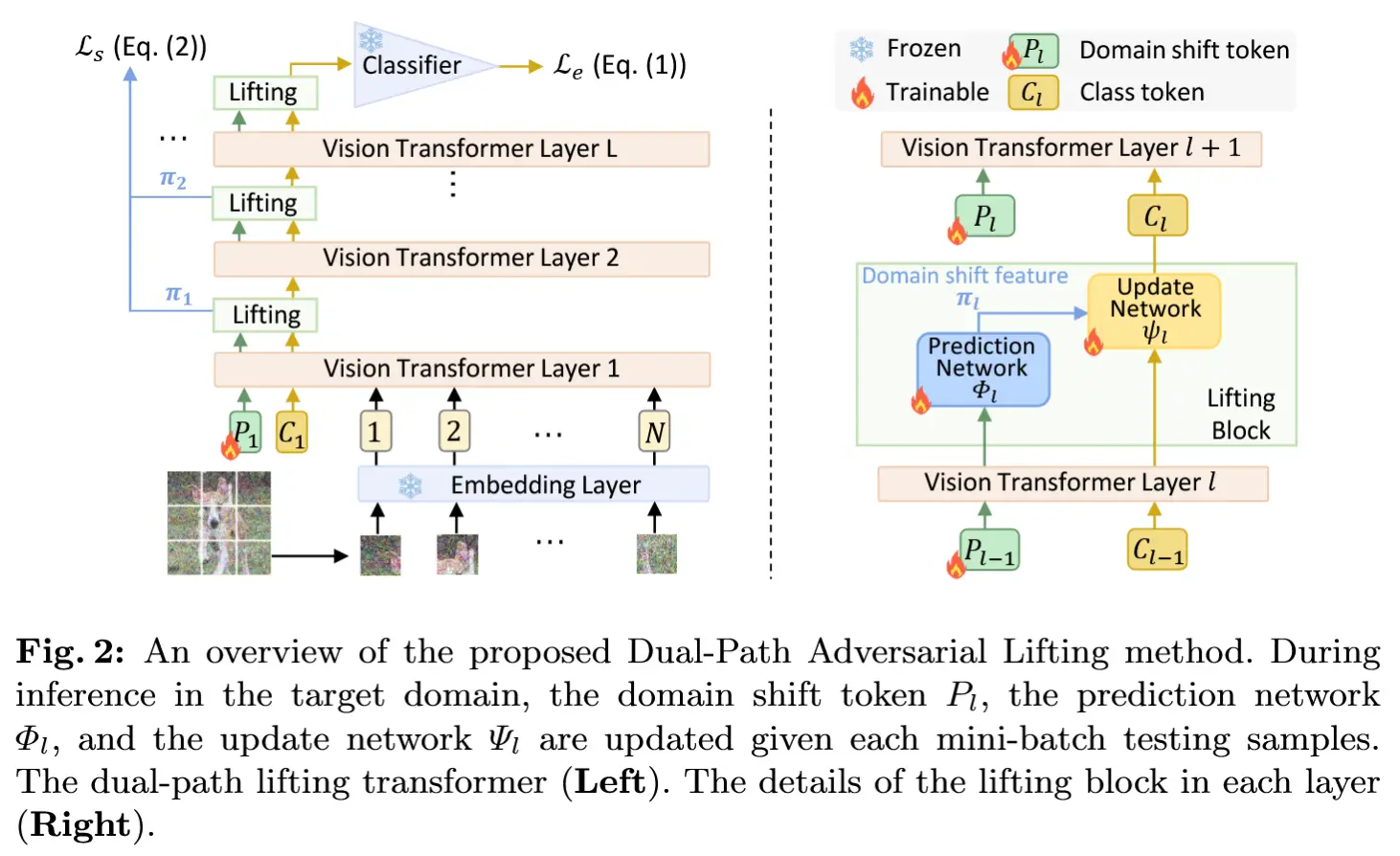
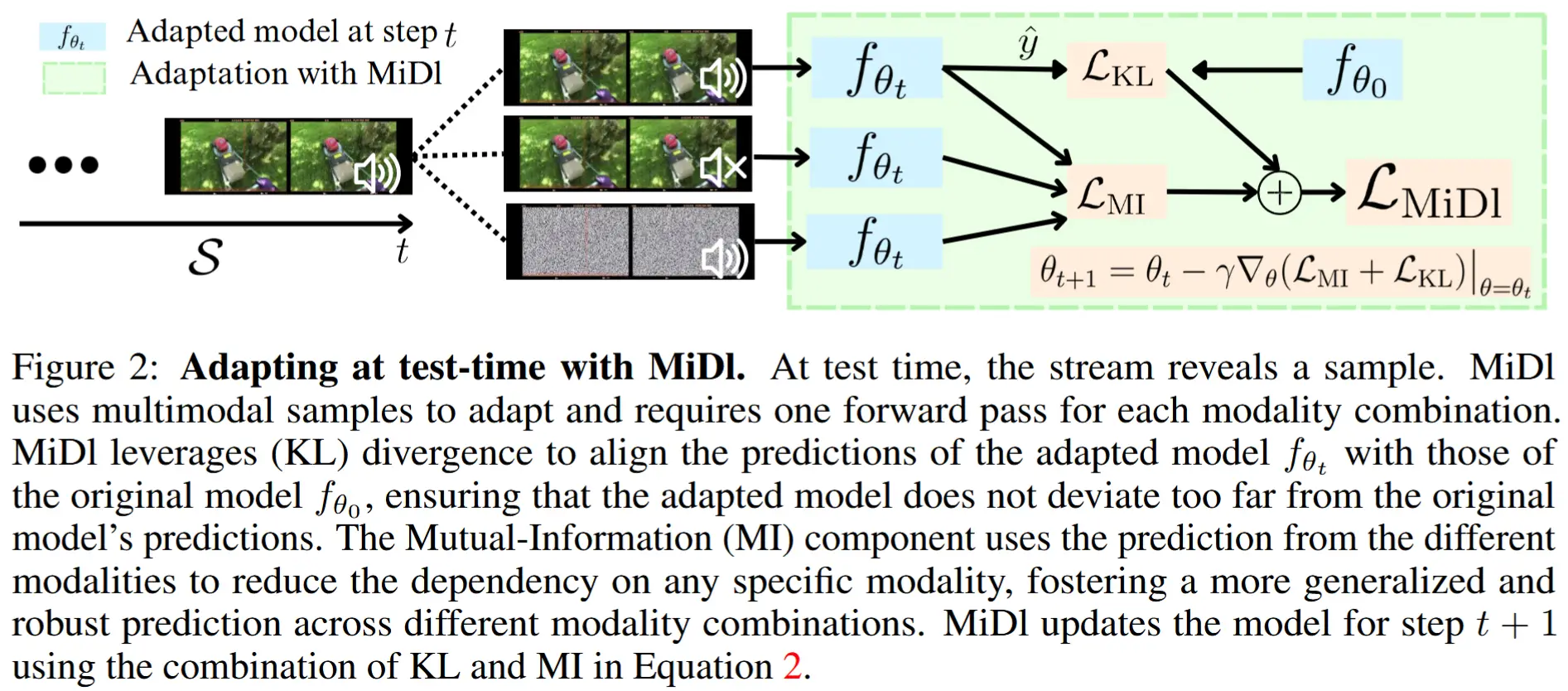
- 论文 - 《Test-Time Model Adaptation with Only Forward Passes》
- 代码 - Github
- 关键词 - TTA、无反向传播、图像分类、Prompt Tuning、IICML2024Oral
摘要
- 问题背景
- 模型通常部署在资源受限的设备上(如 FPGA),并且经常被量化和硬编码为不可修改的参数以加速推理。鉴于此,现有方法往往不可行,因为它们 严重依赖计算密集的反向传播进行模型更新,而这可能无法被支持。
- 本文方法
- 提出了一种测试时间前向优化自适应(FOA)方法,仅通过 无导数的协方差矩阵自适应进化策略 来学习新增的提示(作为模型输入)。
- 为了使该策略在我们的在线无监督设置下稳定运行,作者设计了一种新的适应度函数,通过 测量测试-训练统计差异和模型预测熵 来实现。
- 此外,作者还提出了一种 激活平移方案,直接调整模型对偏移测试样本的激活值,使其与源训练域对齐,从而进一步提升自适应性能。
- 实验性能
- 在不使用任何反向传播和改变模型权重的情况下,FOA 在 8 位量化的 ViT 上的表现优于基于梯度的 TENT 在 32 位全精度 ViT 上的表现,同时在 ImageNet-C 上实现了高达 24 倍的内存减少。
1 引言
- 根据是否涉及反向传播,现有的 TTA 方法通常可以分为以下两类:
- 无梯度方法
- 通过调整批归一化层中的统计量、校正输出概率或调整分类器等方式从测试数据中学习。
- 优点:这些方法避免了反向传播且不改变原始模型权重,因此本质上降低了对源域遗忘的风险。
- 缺点:无法显式利用模型对给定测试样本的反馈以优化可学习参数,学习能力有限,可能导致在分布外测试数据上的性能不佳。
- 基于梯度的方法
- 包括旋转预测、对比学习、熵最小化等技术。
- 通过在测试过程中在线更新模型参数,利用自监督/无监督学习释放了 TTA 的潜力。
- 局限:在实际部署时仍面临关键挑战,如下表1。
- 无梯度方法

-
动机 / 前人工作不足
- 边缘设备计算能力和内存容量有限,不足以支持 TTA 所需的密集计算,尤其是需要反向传播的。
- 模型量化后的不可微性会导致在多层传播时梯度消失,使得不支持反向传播。
- 在一些为特定模型定制的专用计算芯片上,模型参数通常被硬编码且不可修改。
-
本文方法 - 前向优化自适应 FOA
- 将 协方差矩阵自适应(CMA) 进化策略用于 TTA,无需反向传播的优化器。然而 CMA 难以处理超高维度的优化问题(例如深度模型训练),并且依赖于监督学习信号。因此,我们提出 仅在测试时更新一个新插入的提示(作为模型输入,如图 1 所示),以降低解空间的维度,同时避免修改模型权重。
- Fitness Function:为了使 CMA 在无监督信号的情况下稳定运行,作者设计了一种 新的无监督适应度函数 来评估候选解,该函数包括 模型预测熵 以及 分布外(OOD)测试样本与源分布内(ID)样本之间的激活统计差异。在此过程中,仅需少量 ID 样本来估计源统计量。
- Activation Shifting:为进一步提升自适应性能,作者设计了一种 仅前向的回源激活平移机制,直接调整 OOD 测试样本的激活值,并动态更新从 OOD 测试域到 ID 源域的平移方向。
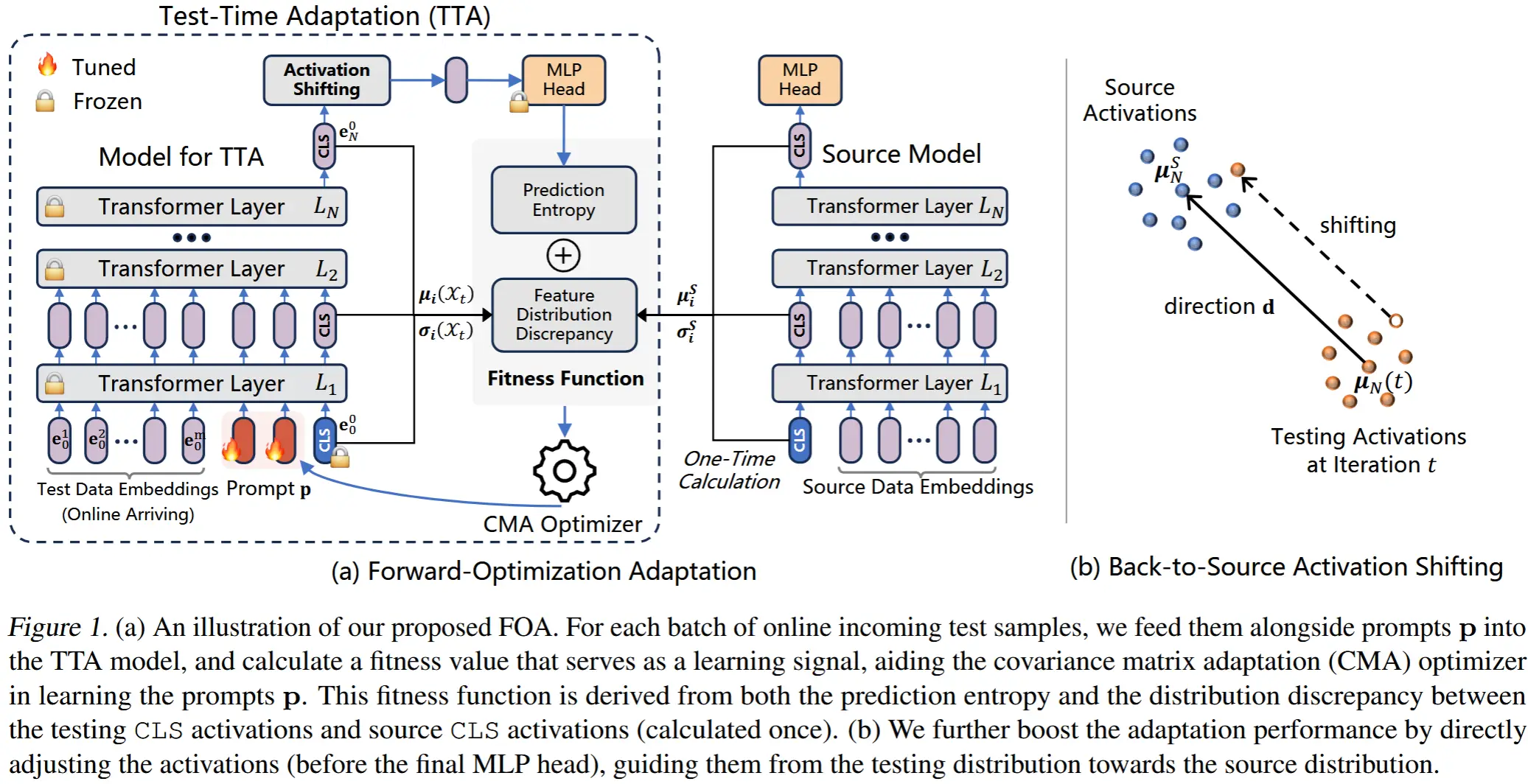
2 方法
在本文中,我们提出了一种新颖的测试时间前向优化自适应方法(FOA),该方法无需更新模型参数,从而提升了测试时间自适应在各种实际场景中的实用性。从图 1 可以看出,FOA 在输入层和输出特征层两个层面进行自适应:
- 输入层 :FOA 插入 一个新的提示 作为模型的输入,并 仅在线更新这一提示 以实现分布外(OOD)泛化,使用 无导数优化器结合专门设计的无监督适应度函数(第 2.1 节)。
- 输出特征层 :一种 回源激活平移策略 进一步增强了自适应性能,通过直接调整最后一层的激活特征,将它们从 OOD 域对齐回源 ID 域(第 2.2 节)。
算法 1 中总结了 FOA 的伪代码。

2.1 前向提示自适应
(引入困难) 直接将 CMA 应用于 TTA 场景是不可行的,原因如下:
- 在 TTA 中,需要更新的模型参数通常是高维的,因为深度模型通常包含数百万个参数。这使得 CMA 难以直接应用于深度模型的自适应。
- 传统的 CMA 方法依赖于有监督的离线学习,即使用真实标签评估候选解。相比之下,TTA 在没有真实标签的情况下运行,并且通常是在线设置,这使得传统 CMA 方法无法适用。
(解决思路) 引入新的提示作为模型的输入进行更新,降低解空间的维度 + 设计了一种无监督适应度函数,为 CMA 优化提供一致且可靠的训练信号。
基于 CMA 的提示适应
受连续提示学习在深度模型微调领域中表现出的有效性启发,作者在模型输入的开始部分(即第一个 Transformer 层之前)添加新的提示嵌入,同时保持所有其他模型参数冻结。通过这种方式,可学习模型参数的维度将显著降低,从而与 CMA 优化兼容。形式上,给定一个测试样本 \mathbf{x} \sim Q(\mathbf{x}) 和一个 ViT 模型 f_\Theta(\cdot) = \text{Head}(L_i(\cdot)) ,我们的目标是找到最优提示 \mathbf{p}^* :
其中, \mathcal{L}(\cdot) 是 Fitness Function, \mathbf{p} \in \mathbb{R}^{d \times N_p} 包含 N_p 个提示嵌入,每个嵌入的维度为 d 。我们通过使用无导数的 CMA 来解决这个问题。
CMA 的适应度函数
(难点) 为了使用 CMA 有效解决公式 (4),主要挑战在于开发一个合适的 \mathcal{L}(\cdot) 来评估给定的解 \mathbf{p} 。
(现有的TTA目标) 一种直接的方法可能是采用现有的 TTA 学习目标,例如预测熵。然而,模型预测在遇到严重损坏的 OOD 样本时具有高度不确定性,此时,基于熵的度量难以为 CMA 优化提供一致且可靠的信号。并且,仅专注于优化熵可能导致提示退化为平凡解。
为了解决这些问题,我们设计了一种新的适应度函数,用于正则化 OOD 测试样本的激活分布统计量(通过优化后的提示前向传播得到),确保它们与分布内(ID)样本的统计量紧密对齐。该适应度函数在分布层面起作用,避免了由不确定预测中固有的噪声引起的问题,从而提供了更好的稳定性。
(源与目标统计量) 在 TTA 之前,我们首先 收集一组小的 ID 源样本 \mathcal{D}_S = \{\mathbf{x}_q\}_{q=1}^Q ,并将它们输入模型以获得对应的分类标记(CLS tokens) \{\mathbf{e}_i^0\}_{i=1}^N 。然后,我们 计算所有源样本中 CLS tokens 的均值和标准差,得到分布内统计量 \{\mu_i^S, \sigma_i^S\}_{i=0}^N 。需要注意的是,我们只需要少量无标签的分布内样本进行计算(例如 ImageNet 数据集上仅需 32 个样本即可)。类似地,我们计算当前测试批次 \mathcal{X}_t 的目标测试统计量 \{\mu_i(\mathcal{X}_t), \sigma_i(\mathcal{X}_t)\}_{i=0}^N 。
基于上述内容,第 t 批测试样本 \mathcal{X}_t 的总体适应度函数由以下公式给出:
其中,N 表示 ViT 的层数,\hat{y}_c 是表示注意力头最终输出 \hat{\mathbf{y}} 的第 c 个元素,而 \lambda 是一个权衡参数。
公式 5 的Fitness function分为以下两个部分:
- 第一部分模型预测的熵。
- 第二部分确保 OOD 样本的特征分布与 ID 样本尽可能接近。
CMA 进化策略
作者没有直接优化提示 \mathbf{p} ,而是使用 CMA 进化策略,因为它是最成功且广泛用于高维连续解空间中非凸黑盒优化的进化算法之一。具体来说,在每次迭代 t (第 t 批测试样本 \mathcal{X}_t ),CMA 从 一个参数化的多元正态分布中采样一组/种群的新候选解/提示(在进化算法中也称为个体):
其中, k=1, \dots, K , K 是种群大小。 \mathbf{m}^{(t)} \in \mathbb{R}^{d N_p} 是第 t 次迭代时搜索分布的均值向量, \tau^{(t)} \in \mathbb{R}_+ 是控制步长的整体标准差,而 \boldsymbol{\Sigma}^{(t)} 是决定分布椭球形状的协方差矩阵。在采样得到提示集合 \{\mathbf{p}_k^{(t)}\}_{k=1}^K 后,我们将每个 \mathbf{p}_k^{(t)} 与测试样本 \mathcal{X}_t 一起输入模型,以获得与 \mathbf{p}_k^{(t)} 相关的适应度值 v_k 。然后,我们基于 \{v_k\}_{k=1}^K 的排名更新分布参数,通过最大化先前候选成功解的似然性来更新分布参数 \mathbf{m}^{(t)} 、 \tau^{(t)} 和 \boldsymbol{\Sigma}^{(t)} 。
3.2 Back-to-Source 激活平移
在本节中,我们提出了一种“back-to-source activation shifting mechanism”,以进一步提升特征层面的自适应性能,特别是在上述在线提示自适应不足的情况下。这种平移方案直接改变了模型在推理过程中的激活值,并且值得注意的是,它不需要反向传播。具体来说,对于一个测试样本 \mathbf{x} ,我们移动其对应的第 N 层 CLS 特征 \mathbf{e}_N^0 (即最终任务头的输入),沿着从分布外域到分布内域的方向进行平移:
其中, \mathbf{d} 是平移方向,\gamma 是步长。
我们将 \mathbf{d} 定义为 从分布外测试特征中心到分布内源特征中心的向量。在我们的在线 TTA 场景中,随着测试样本数量的增加,测试特征的中心会动态变化。因此,我们通过以下方式在线更新平移方向 \mathbf{d} :
其中, \boldsymbol{\mu}_N^S 是第 N 层 CLS 特征 \mathbf{e}_N^0 的均值,计算基于 源分布内样本集 \mathcal{D}_S (与公式 (5) 中使用的相同)。 \boldsymbol{\mu}_N(t) 是通过 指数移动平均 对 顺序到达的测试样本统计量的近似值。我们定义第 t 次迭代(第 t 批测试样本 \mathcal{X}_t )中 \mathbf{e}_N^0 的均值估计为:
其中, \boldsymbol{\mu}_N(\mathcal{X}_t) 是第 N 层 CLS 特征的均值,计算基于第 t 批测试样本 \mathcal{X}_t 。\alpha \in [0, 1] 是移动平均因子,我们将其设置为 0.1。
3 实验
-
数据集:ImageNet-C、ImageNet-R、ImageNet-V2、ImageNet-Sketch
-
模型:
- 使用 ViT-Base 作为源模型
- 模型在 ImageNet-1K 训练集上训练,权重来自 timm 仓库。
- 使用 PTQ4ViT 方法进行 8 位和 6 位量化。
- 对比的 TTA 方法分为两类:
- 无梯度方法:
- LAME:通过调整模型输出概率进行后训练自适应。
- T3A:在测试时更新基于原型的分类器。
- 基于梯度的方法:
- TENT:通过最小化测试样本预测熵优化归一化层的仿射参数。
- SAR:通过主动样本选择和锐度感知优化器进一步优化预测熵。
- CoTTA:通过增强一致性最大化和师生学习方案进行模型自适应。
- 无梯度方法:
- 评估指标
- 分类准确率(%)
- 预期校准误差(ECE,%):衡量概率模型中预测概率与实际结果之间的差异,评估模型预测可信度的重要指标,尤其是在医疗诊断和自动驾驶等场景中。
3.1 全精度模型上
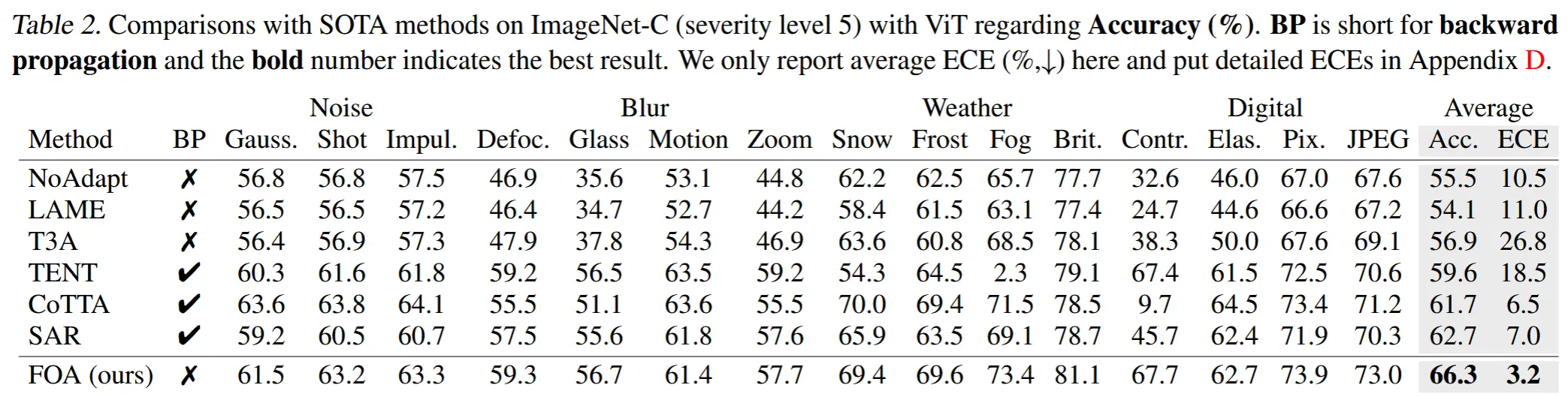
- 表2
- ImageNet-C,全精度 ViT
- FOA 在 15 种不同损坏类型上取得了最佳的平均分类准确率和预期校准误差(ECE),证明了其有效性。
- 无梯度方法(如 LAME 和 T3A)仅获得轻微的性能提升,甚至表现更差。
- FOA 的平均 ECE 显著低于基于反向传播的方法,这主要得益于 FOA 的激活分布正则化(公式 (5)),缓解了先前方法因使用不精确伪标签或熵进行学习而导致的误差累积问题。
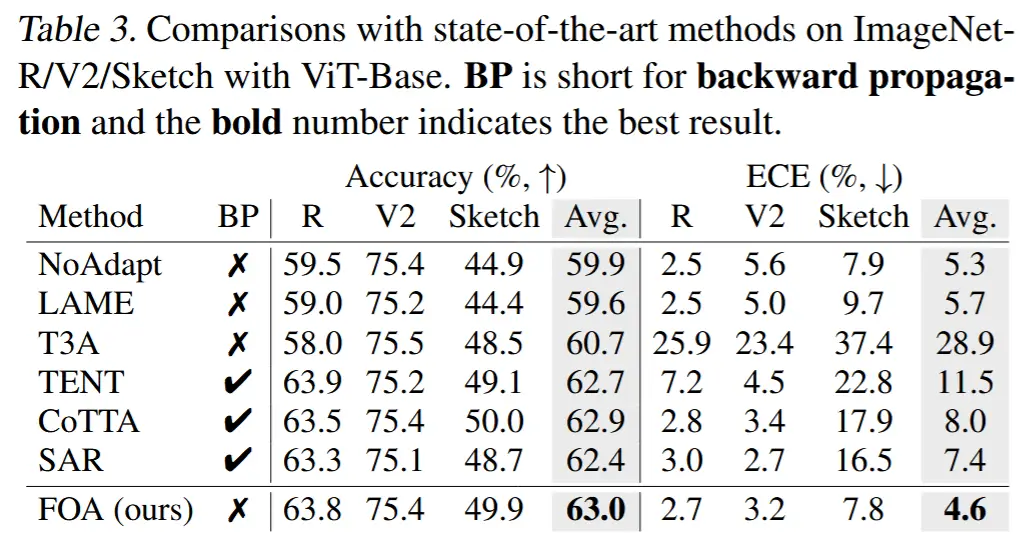
- 表3
- 在 ImageNet-R/V2/Sketch 上的结果。
- FOA 取得了最佳或与现有方法相当的性能,进一步验证了 FOA 在多种分布外(OOD)场景下的有效性和鲁棒性。
3.2 量化模型上
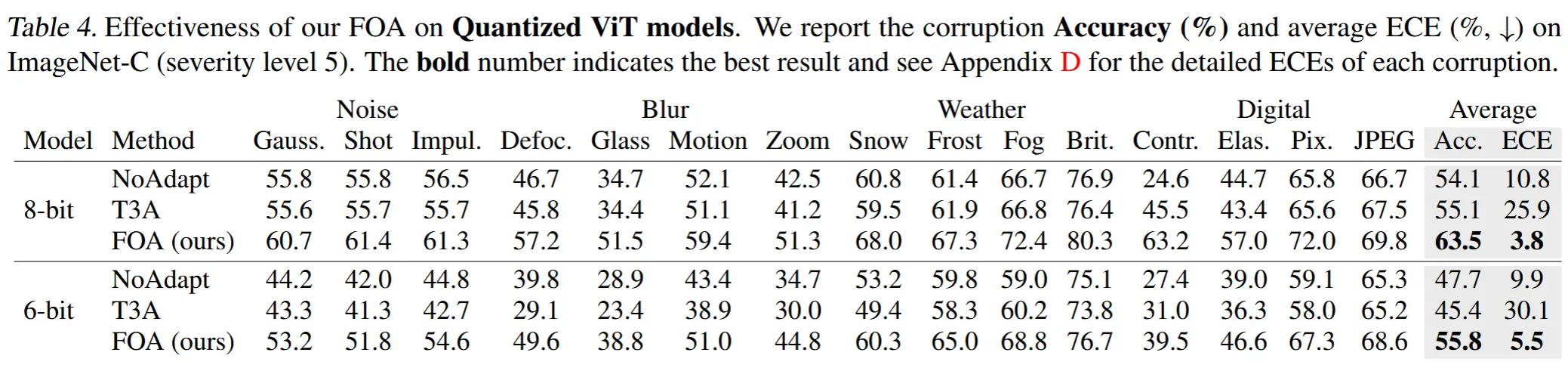
- 表4
- 传统的基于梯度的 TTA 方法(如 TENT、CoTTA 和 SAR)在这些场景下不可行,因此不参与比较。
- 将 FOA 应用于 8 位和 6 位量化的 ViT 模型,并与无梯度方法 T3A 进行对比。
- 实验结果如表3,FOA显著优于无梯度方法 T3A。
3.3 消融实验
- FOA 组件的有效性分析
- 两个关键组件:激活分布差异(Activation Discrepancy)适应度函数 与 激活平移机制(Activation Shifting Scheme)。
- 结果如表5。

后续作者还做了充分的实验和讨论,不一一介绍了,包括以下实验和讨论:
Effects of Population Size K in CMA (Eqn. (6))
Effects of Number of Prompt Embeddings Np in FOA.
Effects of #Samples (Q) for Calculating \{μ^S_i , σ^S_i\}^N_{i=0}
Results on Single Sample Adaptation (Batch Size = 1)
Run-Time Memory Usage
Computational Complexity Analyses.
Effects of Design Choice w.r.t. Learnable Parameters, Optimizer and Loss.
Effectiveness on ResNet and VisionMamba
Effectiveness under Non-i.i.d. Scenarios.
Comparison w.r.t. In-Distribution Performance.
Differences from Previous Forward-Only TTA