论文笔记《Test-Time Model Adaptation for Visual Question Answering...》

论文笔记《Test-Time Model Adaptation for Visual Question Answering...》

Administrator 9 2025-04-02

摘要

  • 问题背景
    • 视觉问答 (VQA) & 测试时适应 (TTA)
    • 简单地将现有的 TTA 方法（例如熵最小化）引入 VQA 并不完美，且只能带来微小的性能提升。原因在于，先前的方法没有考虑到 VQA 问题的特殊性质，并忽略了以下两点：1）数据集中存在的偏差样本可能对测试时间模型自适应产生负面影响； 2）模型可能已经捕捉到了数据集中的偏差。
  • 本文工作
    • 提出了针对 VQA 模型自适应的测试时间去偏自监督（Test-time Debiased Self-supervised, TDS）学习目标。
    • 具体而言， 仅对无偏见的测试样本 执行熵最小化，以提高模型在测试时的适应能力。为了识别这些无偏样本，作者为每个测试样本 构造一个负样本，然后将 输出答案不同 的测试样本视为无偏样本，即当测试样本和相应的负样本输入 VQA 模型时，如果其输出答案不同，则该测试样本被认为是无偏的。
    • 同时，本文还从自适应过程中 移除那些预测熵较高的样本，从而使测试时间梯度更加可靠。
    • 为了防止模型 过度拟合偏差样本的表面相关性，本文利用偏差样本及其对应的负样本来辅助自适应过程。
  • 实验
    • 在 VQA-CP v1 和 VQA-CP v2 数据集上的大量实验表明了本文提出的 TDS 方法的有效性。

1 引言

  • 完全测试时自适应背景

    • 主要在图像分类领域，解决类似的分布偏移问题。
    • 这些方法能够在线地对任何预训练模型进行自适应，无论是小批量还是单个测试样本，并显著提升模型在分布外（OOD）测试数据集上的性能。

  • TTA on VQA 面临的挑战

    1. 这些方法忽略了测试时间自适应过程中的偏差 (biases) 问题 。由于大多数机器学习数据集不可避免地包含偏差，最小化偏差样本的熵以更新模型可能会对模型性能产生负面影响。（例如，在图 1 中，VQA-CP v2 数据集存在严重的偏差问题）
    2. 这些方法忽略了模型可能已经捕捉到了数据集中的偏差。在测试时间自适应过程中缓解偏差问题是重要的，这可以促进模型利用推理能力来回答问题。然而，如何在测试时缓解偏差仍然是一个开放性问题。（如图 1 所示，Updn 模型已经捕捉到了训练集中的偏差）。

偏差问题 ：指 VQA 模型通过捕捉问题和答案之间的捷径来回答问题，而未考虑图像信息。

paper26-1.webp

  • 本文工作
    • 提出一种名为 测试时间去偏自监督（Test-time Debiased Self-supervisions, TDS） 的方法，以在测试时提升模型在 OOD 数据集上的性能。
    • 首先，识别偏差样本，通过在小批量数据中随机采样一张图像 \hat{v}_i 来 构造负样本。然后，如果输入样本及其对应负样本后模型输出的 答案相同，则将这些样本视为偏差样本。
      • 动机：从偏差问题的定义可以知道，给定偏差样本 (v_i, q_i) 及其对应的负样本 (\hat{v}_i, q_i)，VQA 模型可能会输出相同的答案。
    • 此外，本文在模型自适应之前设置一个阈值来 过滤掉高熵样本，以提高自适应的稳定性。
    • 最后，为了在测试时缓解偏差，本文考虑 抑制模型过度拟合偏差样本的表面相关性，这可以 通过最小化偏差样本及其对应负样本答案预测的可能性 来实现。

2 相关工作

2.1 VQA

  • VQA任务方法可以分成三类
    • 基于注意力机制的方法
    • 基于图学习的方法
    • 基于知识的方法]
  • VQA 基准数据集
    • VQA v1：不可避免包含偏差，例如对于问题类型“Do you see a . . . ”，只需回答“yes”，而不考虑问题的其余部分和图像信息，就能获得约 87% 的准确率。
    • VQA v2：在VQA v1基础上通过收集补充图像平衡而成。然而，这些数据集仍然包含容易被 VQA 模型捕捉到的表面相关性。
    • VQA-CP v2：为进一步评估 VQA 模型的真实推理能力，Agrawal 等人通过重新组织 VQA v2 数据集的训练集和验证集，构建的一个分布外（OOD）数据集。

2.2 VQA 中的偏差

  • 为缓解 VQA 中的偏差问题，一些方法试图在训练阶段引入去偏技术。这些方法可以根据是否采用数据增强技术分为两类：
    • 无数据增强的方法：直接削弱语言偏差或增强视觉表示
      • 一些方法 [12], [17], [30], [36] 在训练时构建额外的单模态分支以捕捉需要去除的偏差，但这种方法引入了额外的计算开销。
      • CF-VQA [30] 甚至在推理阶段引入了额外的参数。
      • 为使 VQA 模型更专注于视觉或文本信息，一些方法 [32], [33] 引入基于人工标注的辅助训练过程，以加强视觉对齐。
    • 基于数据增强的方法
      • CSS-VQA [29] 和 Mutant [37] 方法通过分别遮挡图像中的重要对象和问题中的关键词生成大量反事实样本，以辅助训练过程。
      • 为了减少对昂贵标注的依赖，一些方法 [34], [35], [36], [38] 基于可用样本构建负样本以平衡数据集。
  • 本文不同之处
    • 在TTA视角下缓解偏差问题。
    • 不同于训练时的方法使用测试集选择最佳模型，测试时的 OOD 分布是未知的，因此部署模型的选择是不含未来因素的，本文目标是基于测试数据在测试时缓解数据集偏移。

2.3 测试时适应

  • TTA 相关工作
    • Tent [14] 提出了完全测试时间自适应方法，其中作者提出最小化测试样本的无监督熵。
    • 基于 Tent，MEMO [16] 采用数据增强技术对图像进行增强，并使用这些增强样本更新模型。
    • DDA [48] 提出首先使用扩散模型缓解图像的分布偏移，然后对处理后的样本进行预测而无需更新模型。
    • TPT [42] 提出通过样本熵指导提示参数（prompt parameters）的自适应以提升 CLIP [49] 模型的性能。
    • CoTTA [43] 考虑了一种新的持续测试时间自适应设置，即目标域分布可能随时间变化，并设计了一种新方法来解决该设置中的误差累积和灾难性遗忘问题。
    • 受最终遇到条件固有不确定性的启发，LAME [44] 提出了拉普拉斯调整最大似然估计目标，通过凹凸程序调整模型输出来实现这一目标。
  • 在本文工作中，作者考虑了视觉问答（VQA）问题的特殊性质，并设计了一种高效的完全测试时间自适应方法用于 VQA。

3 问题定义

（问题描述） 在视觉问答任务中，许多模型在独立同分布（IID）数据集上表现出色，但在训练和测试阶段答案分布不同时，性能会严重下降。这种现象阻碍了部署的 VQA 模型在遇到不同答案分布的数据时的实际应用。

为缓解这一问题，本文研究如何仅基于预训练的 VQA 模型和测试数据（无需测试标签和源训练数据）在测试时对预训练的 VQA 模型进行自适应，以提升模型性能。

（符号描述） 假设 M_{\theta_p} 是一个在标注训练数据 \mathcal{D}_s = \{(v_i, q_i, a_i)\}_{i=1}^{N_s} 上预训练的 VQA 模型，其中 \theta_p 表示预训练 VQA 模型的参数。在某些情况下，我们可能无法访问源数据。此外，测试数据 \mathcal{D}_t = \{(v_j, q_j)\}_{j=1}^{N_t} 并未提供真实标签。因此，我们的目标是 仅使用测试数据来提升模型在分布外（OOD）测试集上的性能，这可以公式化为：

\min_{\theta_p} -\frac{1}{N_t} \sum_{j=1}^{N_t} \mathcal{L}((v_j, q_j); \theta_p),

其中， (v_j, q_j) \in \mathcal{D}_t ，且 \theta_p 是需要更新的 VQA 模型的参数。


4 基于去偏自监督的测试时间 VQA 模型自适应

TDS 方法大致思路

（熵最小化） 具体而言，为了将预训练的 VQA 模型 M_{\theta_p} 适配到 OOD 测试集，一种直观的方法是将学习目标 \mathcal{L}(\cdot) 视为一个熵最小化问题，即：

\min_{\theta_p} \frac{1}{N_t} \sum_{j=1}^{N_t} E((v_j, q_j); \theta_p) \\= \min_{\theta_p} -\frac{1}{N_t} \sum_{j=1}^{N_t} \sum_{a \in \mathcal{A}} M_{\theta_p}(a|v_j, q_j) \log M_{\theta_p}(a|v_j, q_j), \tag{2}

其中， A 表示候选答案的集合。

（偏差问题） 然而，大多数机器学习数据集不可避免地包含偏差。VQA 模型可能会捕捉这些偏差，而不是学习推理能力。

（解决办法） 作者采用了下面三种技术：

  1. 过滤偏差 在使用样本熵对模型进行自适应之前，需要过滤掉偏差样本。
  2. 高熵样本 此外，并非所有用于更新模型的样本熵都是有益的，因此进一步过滤掉预测熵较高的样本。
  3. 直接抑制VQA模型 作者还提出在测试时抑制 VQA 模型从偏差样本中学习偏差。

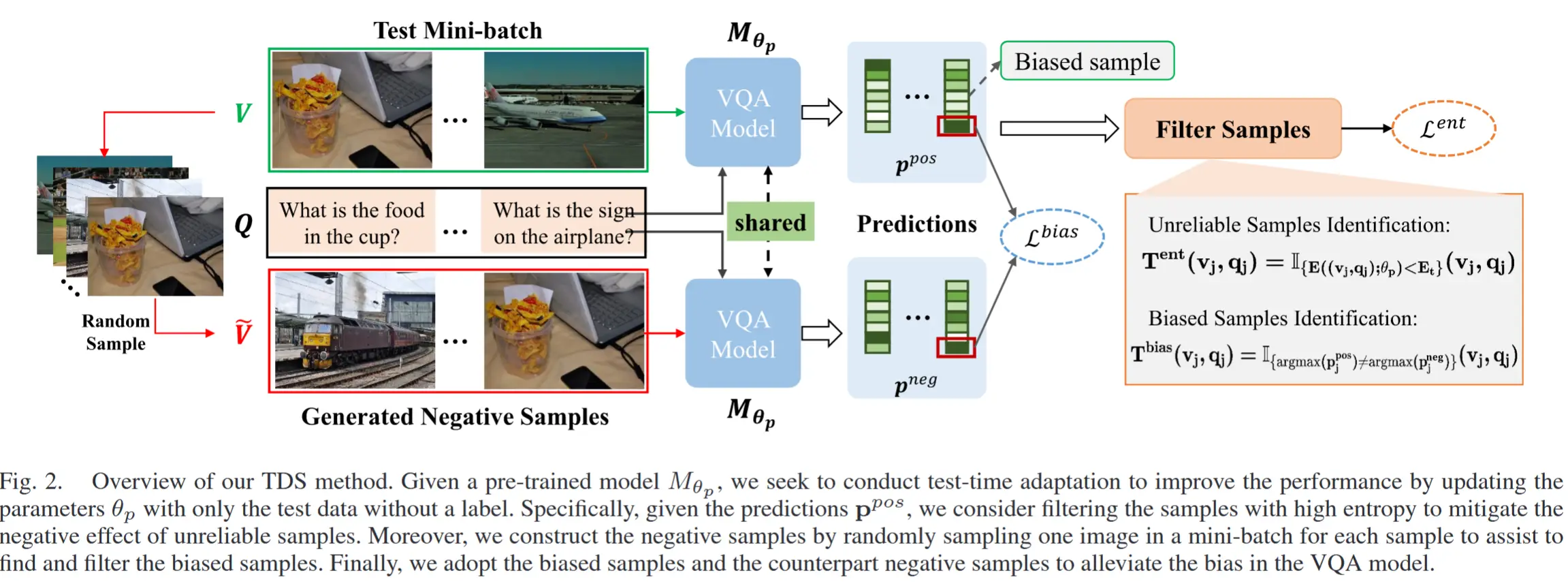
框架如图 2 所示

paper26-2.webp

4.1 选择性测试时熵最小化

4.1.1 偏差样本识别

（动机/观察） 一般来说，偏差问题通常指问题和答案之间的表面相关性。换句话说，模型倾向于在不关注图像的情况下回答问题。从这个角度来看，给定一个测试样本对 (v_j, q_j)，当回答问题 q_j 时，如果该样本是偏差样本，那么无论输入的是哪张图像，VQA 模型都会输出相似的预测结果。

（方法设计） 给定一个测试数据的小批量 \{(v_j, q_j)\}_{j=1}^B ，对于每个样本 (v_j, q_j)，我们通过从图像小批量 \{v_j\}_{j=1}^B 中随机采样一张图像 \tilde{v}_j 来构建负样本 (\tilde{v}_j, q_j) 。将测试样本和对应的负样本输入到 VQA 模型中，我们会得到两种类型的预测 \mathbf{p}^{pos} 和 \mathbf{p}^{neg} ，即：

\mathbf{p}_j^{pos} = M_{\theta_p}(\mathcal{A}|v_j, q_j), \quad \mathbf{p}_j^{neg} = M_{\theta_p}(\mathcal{A}|\tilde{v}_j, q_j). \tag{3}

然后，当两个预测的 top-1 答案相同时，将这些样本视为偏差样本。因此，公式化为：

\mathbf{T}^{bias}(v_j, q_j) = \mathbb{I}_{\{\argmax(\mathbf{p}_j^{pos}) \neq \argmax(\mathbf{p}_j^{neg})\}}(v_j, q_j), \tag{4}

其中， \mathbb{I}(\cdot) 是一个指示函数。通过这种方式，我们在TTA过程中能够缓解偏差样本的负面影响。

注意，是两个预测不等于时 T^{bias} = 1 ，即非偏差样本时值为1。

（负样本构造方法） 需要注意的是，当测试批次大小 B 等于 1 时，我们通过生成与图像特征相同大小的 高斯噪声 来为单个测试样本构造负图像 \tilde{v}_j 。


4.1.2 不可靠样本识别

（动机） 熵较高的样本表明 VQA 模型对这些样本的预测是不确定的。因此，这些样本的熵损失生成的梯度可能是不可靠的。

（高熵样本排除） 引入了一个预定义的熵阈值 E_t 来过滤高熵样本，公式化为：

\mathbf{T}^{ent}(v_j, q_j) = \mathbb{I}_{\{E((v_j, q_j); \theta_p) < E_t\}}(v_j, q_j), \tag{5}

其中，E((v_j, q_j); \theta_p) 表示模型 M_{\theta_p} 对样本 (v_j, q_j) 预测得到的熵。\mathbb{I}(\cdot) 是一个指示函数。通过这种方式，我们能够仅保留相对可靠的样本来在测试时更新模型。

注意，是低于阈值时 T^{ent} = 1，即可靠样本值为1。

（阈值设定） 需要注意的是，阈值 E_t 可以基于候选答案的数量 C 进行定义，即：E_t = \alpha \ln C，其中，\alpha \in [0,1] 是一个超参数，用于调整熵的阈值。


4.1.3 选择性熵损失

（合并表示选择性熵损失） 根据公式 (4) 和 (5)，选择性熵损失 \mathcal{L}^{ent} 计算如下：

\mathcal{L}^{ent} = \frac{1}{N_t} \sum_{j=1}^{N_t} T^{ent} (v_j, q_j) T^{bias} (v_j, q_j) E((v_j, q_j); \theta_p). \tag{6}

4.2 实例级测试时偏差缓解

不同于上述方法对样本进行筛选，本部分尝试直接在 VQA 模型中缓解偏差。

（动机） 尽管在 4.1.1 小节已经找到了偏差样本，但由于模型对样本的不确定性，一些偏差样本可能是 伪偏差（pseudo bias） 。即对于高熵样本时，可能会由于模型的不确定性而得到负样本和测试样本相似的输出，导致这些样本被认为是偏差样本。因此，偏差样本可能具有两个特征，即：

  1. 这些样本应该是可靠的，即这些样本的熵较低；
  2. 将 VQA 模型输入初始样本和对应的负样本，分别得到相同的答案。

第一个特征就是用于排除伪偏差，确保偏差样本的熵低。


（重新定义偏差样本函数） 通过这种方式，我们可以通过以下公式获得真正的偏差样本：

\mathbf{\tilde{T}}^{bias}(v_j, q_j) = \mathbf{T}^{ent}(v_j, q_j) (1 - \mathbf{T}^{bias}(v_j, q_j)).

批注：这个公式似乎有问题，原文前面给出的定义是 T^{ent} = 1 表示低熵样本，T^{bias} = 0 表示偏差样本，个人觉得应该改成

\mathbf{\tilde{T}}^{bias}(v_j, q_j) = (1 - \mathbf{T}^{ent}(v_j, q_j)) \cup \mathbf{T}^{bias}(v_j, q_j)

（去偏损失） 通常来说，偏差问题是指 VQA 模型过度拟合了问题和答案之间的表面相关性。为了缓解这种偏差，受到 [34]、[35]、[36] 的启发，在向 VQA 模型输入偏差测试样本和对应的负样本时，试图阻止 VQA 模型正确回答问题。这可以通过最小化对真实答案的预测来实现。

然而，由于我们无法获取测试样本的真实答案，我们将具有最高得分的预测结果作为伪标签，即：

k = \arg\max (\mathbf{p}_j^{pos}). 在这种情况下，去偏损失函数 \mathcal{L}^{d\_bias} 可表示为：

\mathcal{L}^{d\_bias} = \mathbf{\tilde{T}}^{bias}(v_j, q_j) \text{softmax}(\mathbf{p}_j^{pos})[k] + \mathbf{\tilde{T}}^{bias}(v_j, q_j) \text{softmax}(\mathbf{p}_j^{neg})[k]. \tag{7}

需要注意的是，对于公式（7），如果 k 对应于真实答案，第一项可以有效缓解偏差（即不过度拟合表面相关性），第二项可以促使 VQA 模型更关注图像，因为当提供不匹配的问题和图像时，模型无法正确回答问题。

好巧妙的去偏损失函数

（总损失函数） 总的来说，本文方法主要包含两种损失函数，即选择性熵损失 \mathcal{L}^{ent} 和去偏损失\mathcal{L}^{bias}，其表达式如下：

\mathcal{L}^{total} = \gamma_1 \mathcal{L}^{ent} + \gamma_2 \mathcal{L}^{d\_bias}. \tag{8}

在所有实验中，设定 \gamma_1 = \gamma_2 = 1.0 ，作者并未进行任何超参数调优，这表明该方法对超参数不敏感。


5 实验

5.1 实验设定

  • 数据集： VQA-CP v1 和 VQA-CP v2
  • 基线
    1. Tent：通过最小化测试样本的熵来适配模型。
    2. ETA：基于样本熵进行优化，但排除了不可靠和冗余样本的熵。
    3. TPT：通过增强样本的熵指导模型参数调整以提升性能。
    4. CoTTA：使用权重平均和增强平均预测作为伪标签，指导测试时间自适应。
    5. LAME：引入拉普拉斯调整最大似然估计目标，通过凹凸程序调整模型输出。
  • 模型：UpDn、ViLBERT、LXMERT
  • 使用 SGD 优化器，动量设置为 0.9。
  • 图像和问题的特征提取
    • 使用 Faster-RCNN 提取图像中的对象特征（遵循现有去偏方法 [34], [36]）。
    • 每张图像提取前 36 个对象特征，每个特征维度为 2048。
    • 对问题进行截断或填充至固定长度（14），并使用 GloVe 词嵌入（维度为 300）编码每个单词。
  • 候选答案集合
    • 在 VQA-CP v2 数据集中，收集了 2274 个候选答案（训练集中出现次数超过 9 次）。
    • 在 VQA-CP v1 数据集中，收集了 1691 个候选答案。

由于需要算熵（公式 2），需要提前设定候选答案，因此这似乎也不算一个生成任务，有点像分类任务。


5.2 评估结果

5.2.1 定量结果

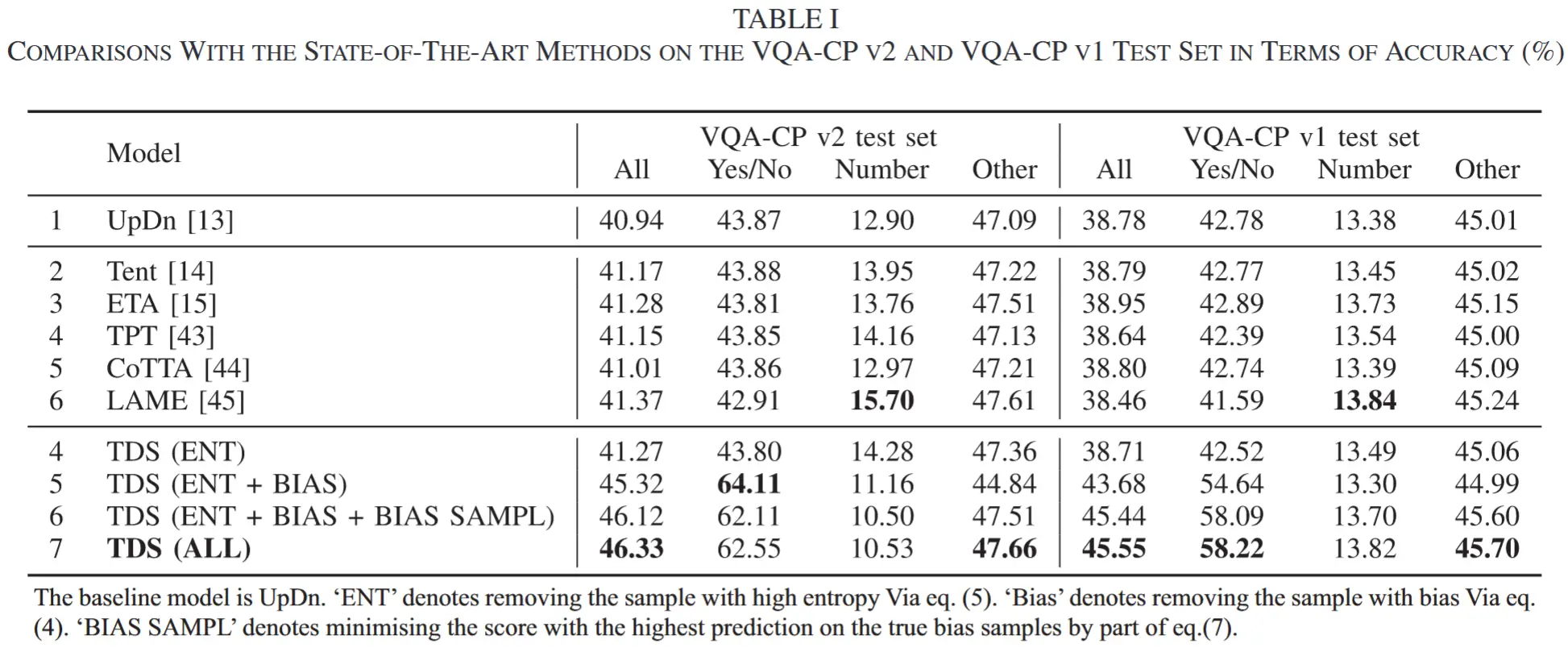
  • 表 1
    • 在 VQA-CP v1 和 VQA-CP v2 上，比较 TDS 与 SOTA 的准确率
    • 在大部分任务中，TDS都优于其他SOTA。（number类任务后面单独分析）
paper26-3.webp

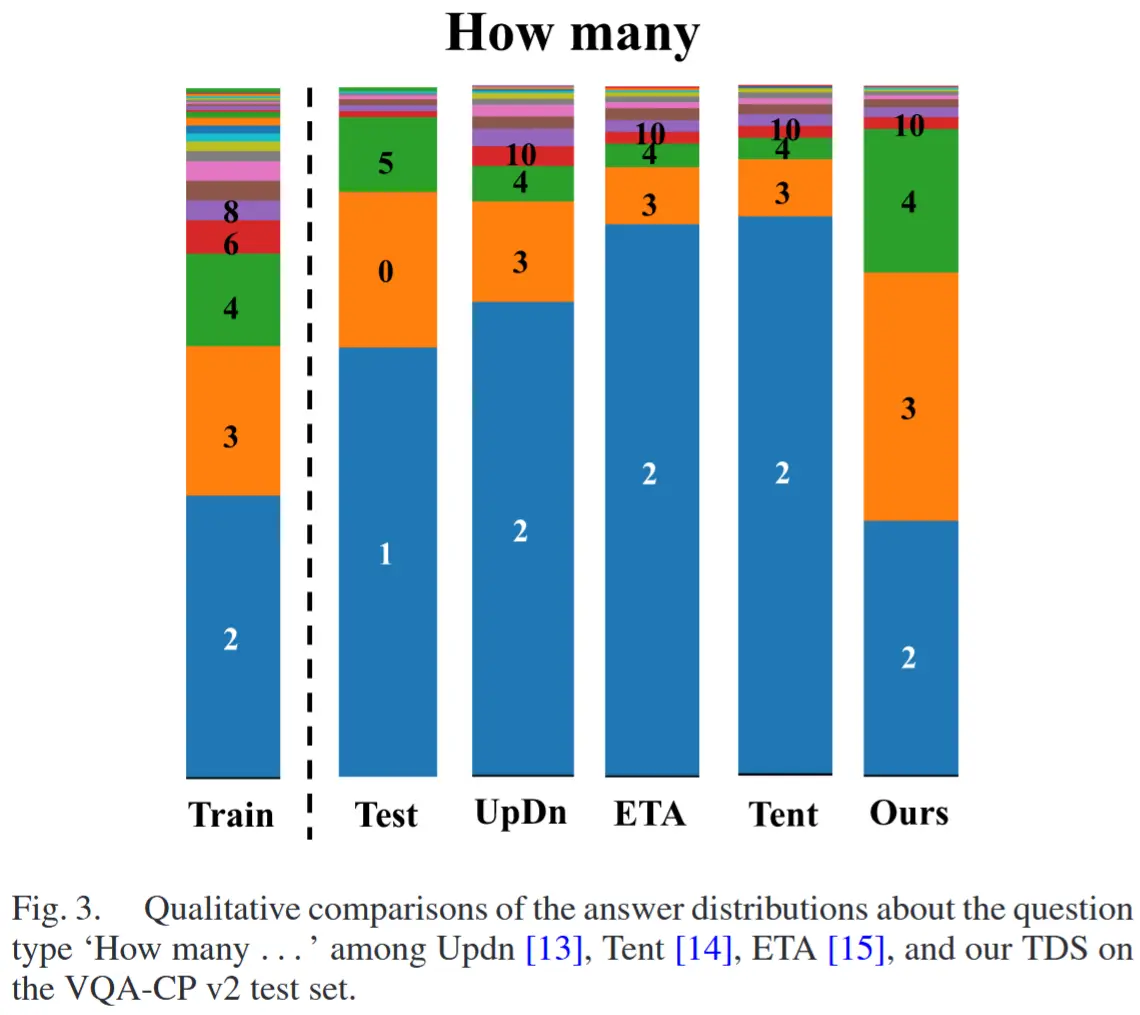
  • 图 3
    • 为了分析Number类型答案性能不佳的原因，作者在图 3 中可视化了问题类型为“How many...”的答案分布。
    • 结果显示
      • ETA 和 Tent 方法忽略了偏差问题，过度拟合了偏差样本，其表现与 UpDn 模型相当。
      • TDS 考虑了偏差问题，因此答案分布与基线模型 UpDn 不同，但由于缺乏真实标签的监督，TDS 在“Number”类型答案上的表现不尽如人意。
paper26-4.webp

5.2.2 定性结果

  • 为进一步展示 TDS 的有效性，作者在 VQA-CP v2 测试集上提供了部分定性结果（见图 4 和图 5）
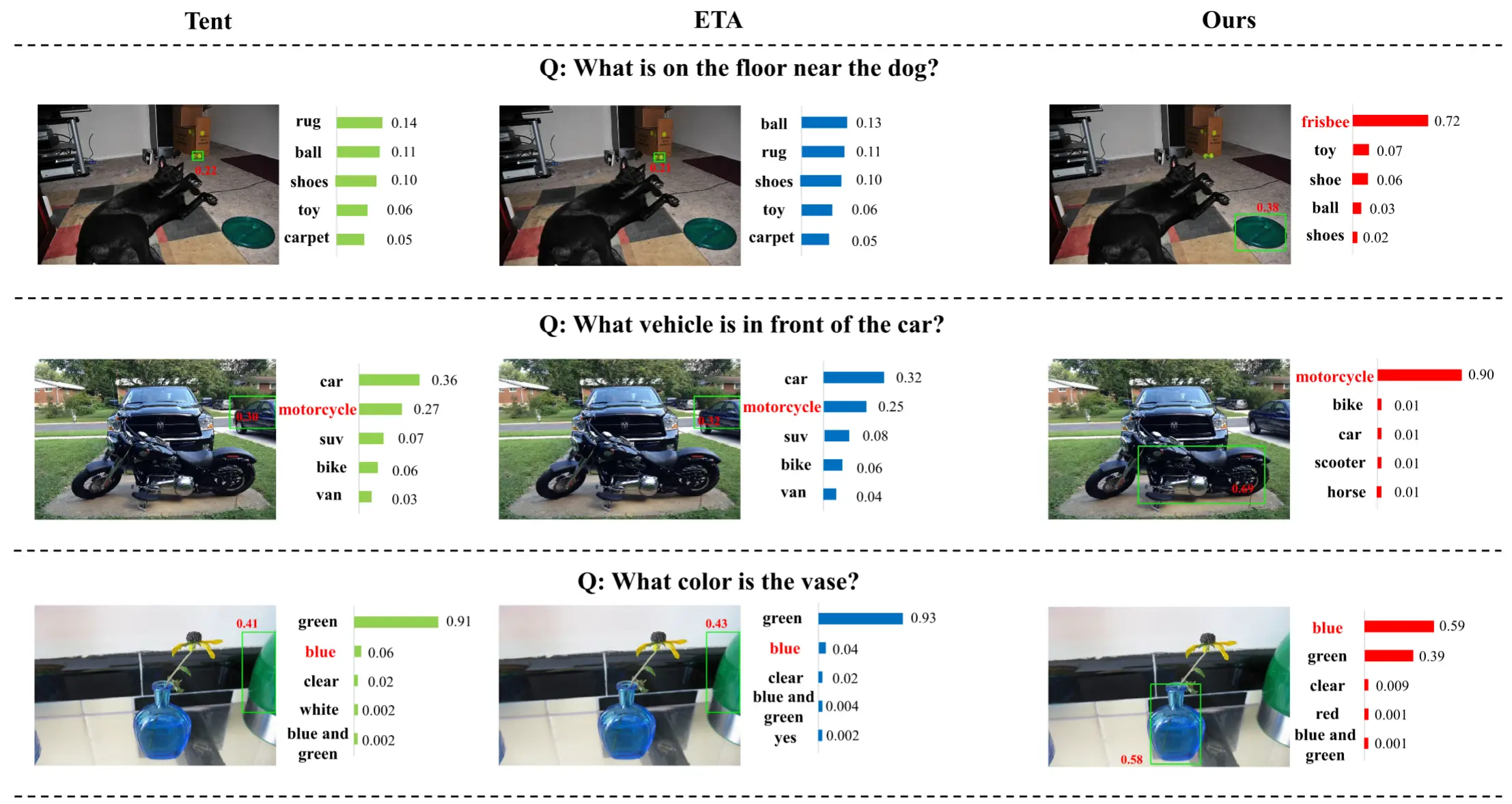
  • 图 4
    • 粗红色是正确答案，横柱是概率。
    • Tent 和 ETA 方法无法在图像中找到目标对象，因此输出了错误答案。
paper26-5.webp

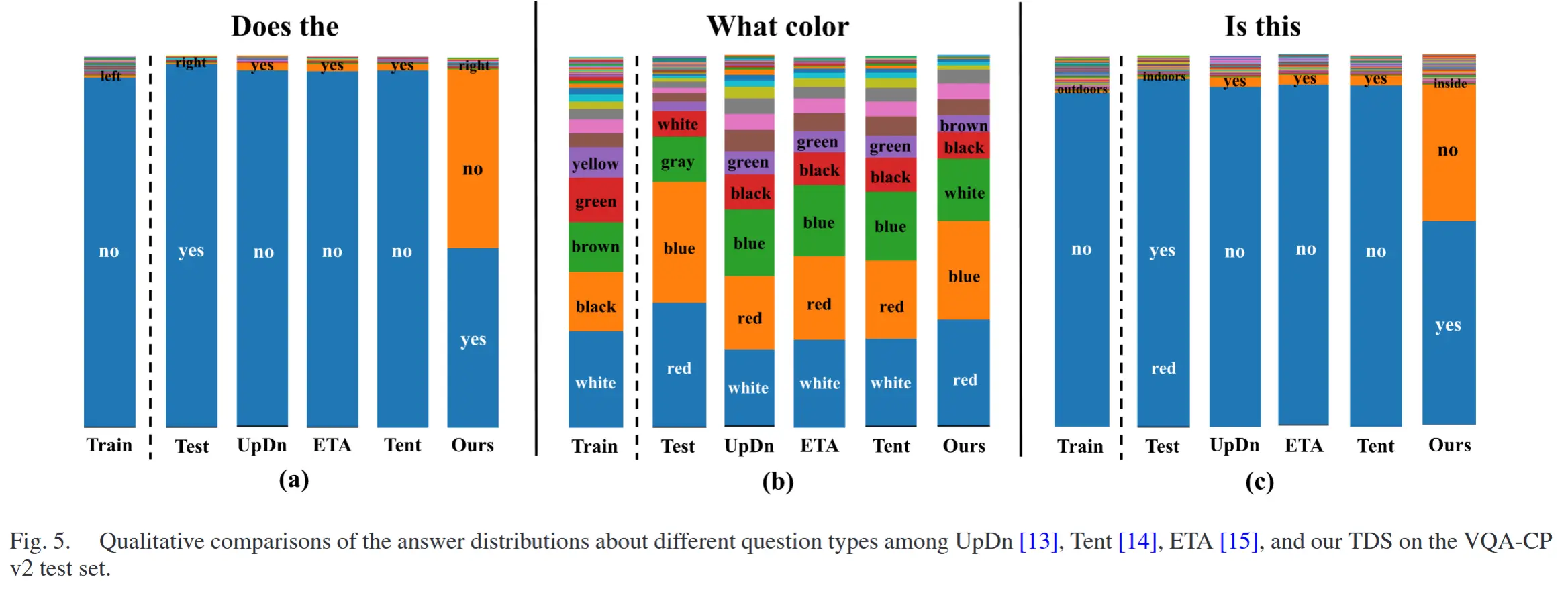
  • 图 5
    • 可视化了不同方法在不同问题类型（即 “Does the...”，“What color...”，和 “Is this...”）下的答案分布.
    • TDS 能够调整从训练集训练的 UpDn 模型的偏差答案分布，使其接近测试集的答案分布。
paper26-6.webp

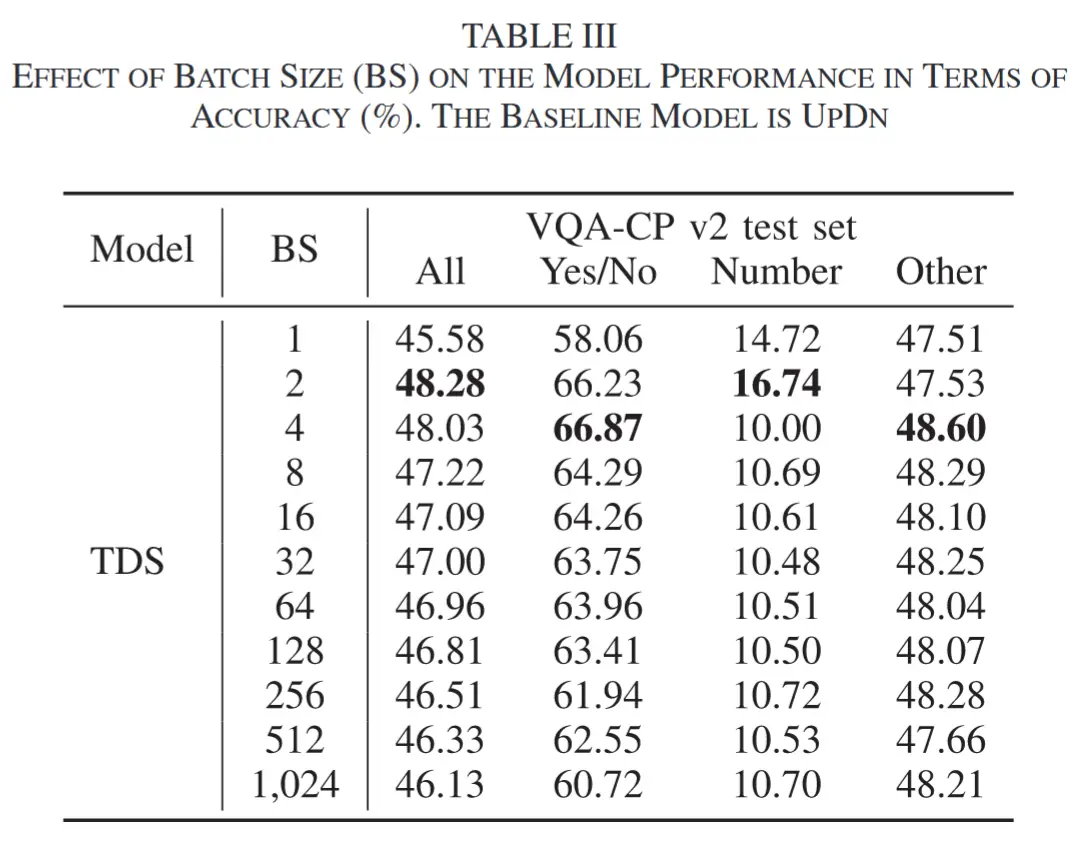
5.3 消融

  • Batch Size 对模型性能的影响
paper26-7.webp

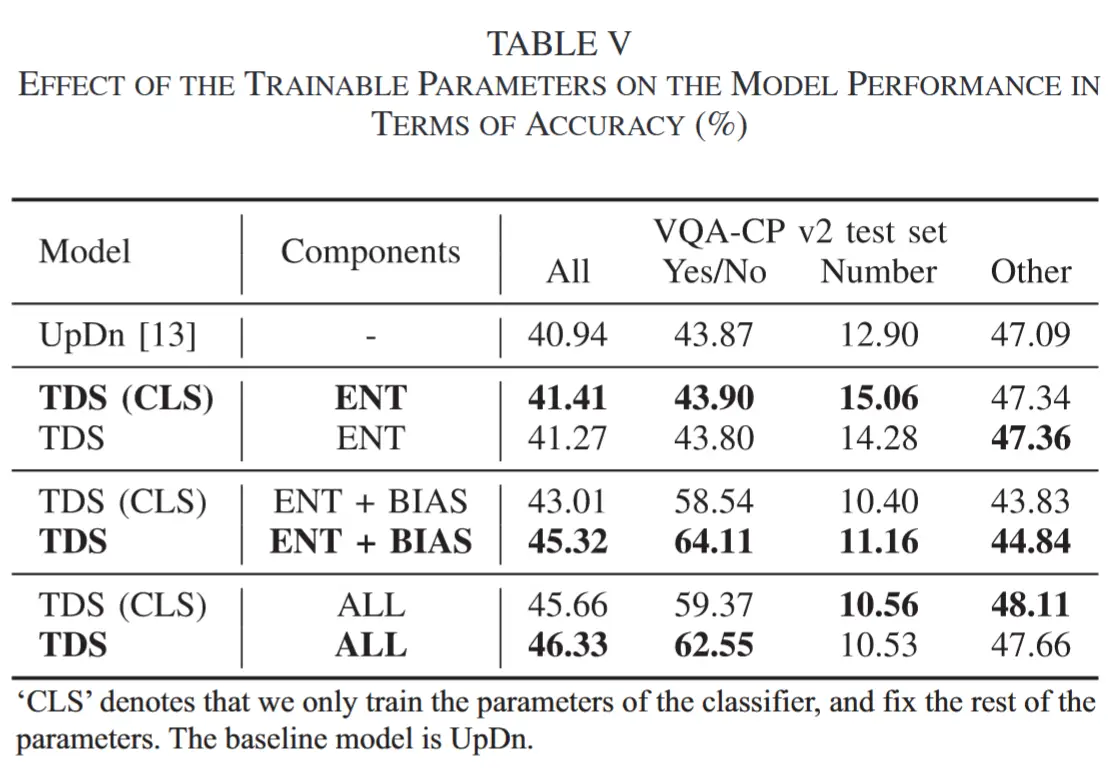
  • 可训练参数的评估
    • 作者引入了一个仅在实验中训练分类器的额外变体，表中的（CLS）。
paper26-8.webp

6 总结

在本文中，作者提出了一种名为 TDS 的新方法，仅使用无标签的测试数据来提升 VQA 模型在测试时的性能。具体来说，为了缓解高熵样本的负面影响，本文设置了一个熵阈值，以过滤掉熵高于该阈值的样本。此外，在测试时进行模型自适应时，偏差问题不可忽视。因此，首先需要识别偏差样本，然后移除这些样本的熵。为了找到偏差样本，为每个样本构建一个负样本，并将输出答案相同的情况（即将样本及其对应的负样本输入 VQA 模型时）视为偏差样本。除了移除偏差样本的熵外，本文还考虑通过使用偏差样本来减轻 VQA 模型中的偏差，即最小化对偏差样本及其对应负样本答案的预测可能性。在 VQA-CP v2 数据集上的大量实验验证了 TDS 方法的有效性。

TTA 论文笔记 多模态