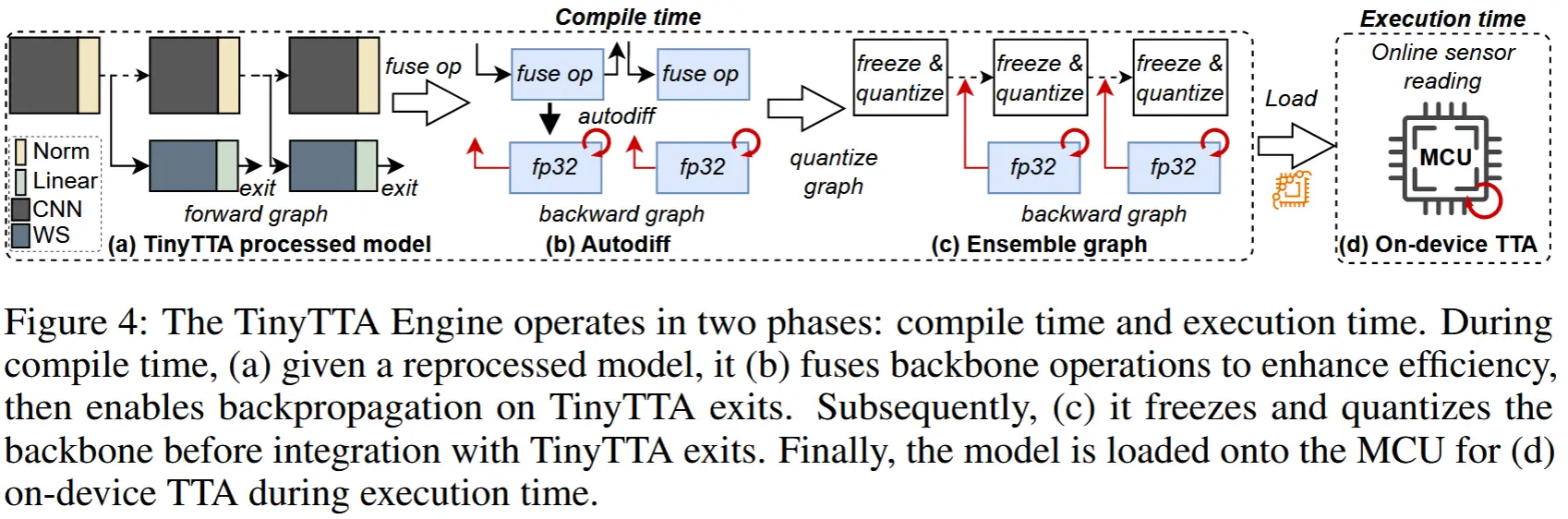
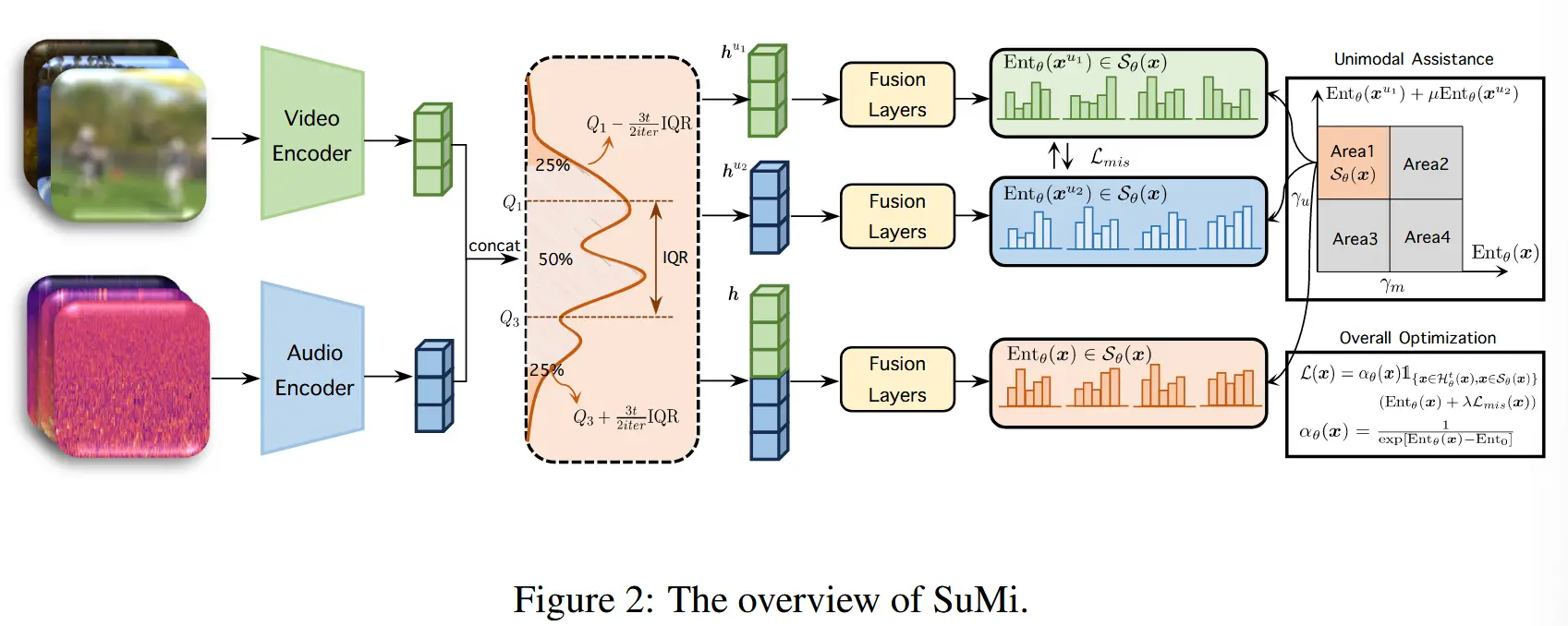
- 论文 - 《Tent: Fully Test-time Adaptation by Entropy Minimization》
- 代码 - Github
- 关键词 - 测试时适应、熵最小化、图像分类
摘要
- 论文背景:测试时自适应 Test-Time Adaptation , TTA。
- 本文工作:提出了一种名为 Tent 的方法,用于在测试阶段对模型进行自适应调整,以提高其在未见过的数据上的泛化能力。Tent 通过最小化预测的熵来优化模型的置信度,并采用在线更新的方式调整模型参数。
- 实验性能:实验表明,该方法在多个任务(如图像分类、数字识别、语义分割等)中均取得了显著的效果,且无需修改训练过程即可在测试阶段完成优化。
1 引言
- 现实世界的应用场景推动了完全测试时间自适应的需求,其背后的原因包括数据、计算和任务的实际需求:
- 可用性 :模型可能因为带宽、隐私或商业利益的原因而被分发,但不附带源数据。
- 效率 :在测试过程中(重新)处理源数据可能会在计算上不切实际。
- 准确性 :如果模型未经自适应调整,可能会因准确性不足而无法满足其设计目的。
- 本文方法
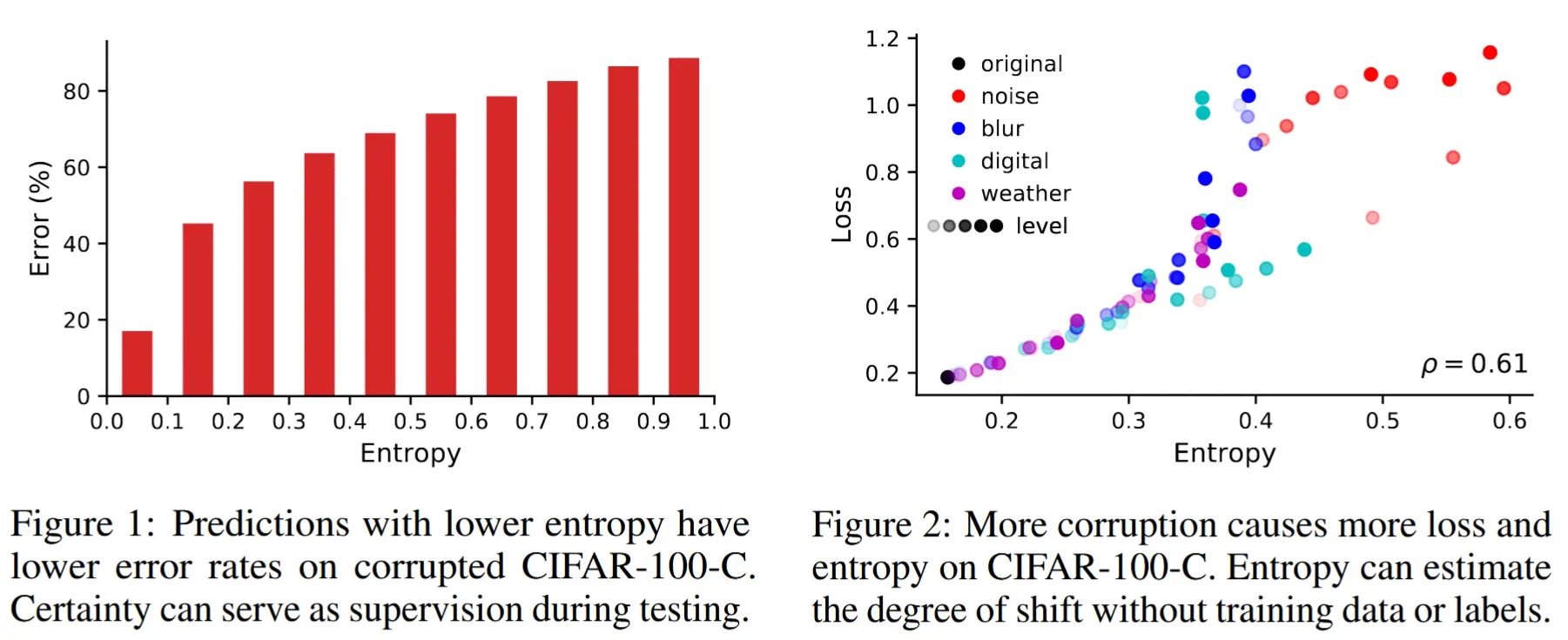
- 为了在测试过程中进行自适应调整,最小化模型预测的熵。作者将这一目标称为 测试熵 ,并以此命名我们的方法为 tent。(如图1和2,阐释了选择熵的理由:熵与误差和数据分布偏移之间的密切联系)
- 为了最小化熵,tent 方法通过对目标数据进行归一化和变换来实现自适应调整。
- 具体来说,tent 通过逐批次估计统计量并优化仿射参数来进行特征调制。这种低维度、逐通道的特征调制方式即使在在线更新的情况下也能高效地适应测试阶段的需求。
- tent 方法不对模型训练施加任何限制或改变:它仅依赖模型参数,而与源数据无关。只要模型能够运行,就可以对其进行自适应调整。
2 场景设定:完全测试时自适应
- TTA的目标是从源域到目标域的泛化。
- 一个在源数据和标签 x_s, y_s 上训练的模型 f_\theta(x)(参数为 \theta)在面对分布偏移的目标数据 x_t 时,可能无法很好地泛化。表 1 总结了不同的自适应场景、所需的数据类型以及损失函数的种类。本文提出的完全测试时间自适应场景独特之处在于,它仅需要模型 f_\theta 和未标注的目标数据 x_t 就能在推理过程中进行自适应调整。

- 现有的自适应方法通常通过更多的数据和监督信号来扩展训练过程:
- 微调迁移学习(Fine-tuning transfer learning)需要目标域的标签 y_t 来通过监督损失 L(x_t, y_t) 进行(重新)训练。而我们的场景不依赖目标域的标签,因此无法使用这种监督训练。
- 域自适应(Domain Adaptation, DA)需要同时使用源域和目标域的数据,通过跨域损失 L(x_s, x_t) 进行训练。然而,我们的场景没有源域数据,因此无法采用这种方法。
- 测试时间训练(Test-Time Training, TTT)在测试阶段进行自适应,但要求在训练阶段联合优化监督损失 L(x_s, y_s) 和自监督损失 L(x_s),以确保参数 \theta 在不同损失之间共享,从而与测试时的自监督损失 L(x_t) 兼容。相比之下,我们的完全测试时间自适应场景独立于训练数据和训练损失,只需给定模型参数 \theta。
3 方法:通过特征调制实现测试熵最小化
- 整体介绍
- Tent 的完整算法需要以下三个要素来定义:一个兼容的模型、一个最小化目标(第 3.1 节),以及一组可优化的参数(第 3.2 节)。
- 图 3 展示了用于完全测试时间自适应的方法框架。

- 被调整的模型必须满足以下条件
- 1)已经针对监督任务进行了训练。(在测试阶段没有提供监督信号,因此模型必须已经完成训练)
- 2)具有概率输出。(为了测量预测的熵,模型需要输出预测的概率分布)
- 3)是可微分的,以便支持快速迭代优化。(梯度优化需要模型具有可微性)
3.1 熵目标
本文方法优化目标 L(x_t) 是最小化模型预测 \hat{y} = f_\theta(x_t) 的熵 H(\hat{y})。具体来说,我们使用香农熵(Shannon, 1948)作为衡量标准,其定义为:
其中,p(\hat{y}_c) 表示类别 c 的预测概率。
需要注意的是,单独优化单个预测会导致一个平凡解:将所有概率分配给最可能的类别。为了避免这种情况,我们通过对共享参数进行批量预测的联合优化来防止这种极端情况的发生。
上面这句话指出了当测试时适应任务中,往往需要比较大的batch,对于小batch会造成上述的平凡解。大batch在这里为什么有效?
- 防止过拟合 :通过联合优化 batch 内的所有预测,模型不会为了某个样本的预测变得过于自信,从而避免了过拟合。
- 提升泛化能力 :这种方法鼓励模型在整个 batch 上生成更加合理和多样化的预测分布,而不是简单地将所有概率集中在某个类别上。
- 自然正则化 :通过 batch 内的联合优化,模型参数被限制在一个更合理的范围内,起到了正则化的作用。
熵是一个 无监督的目标,因为它仅依赖于模型的预测结果,而不需要标注数据。
3.2 调制参数
(为什么不修改模型参数 \theta)
- 在 TTA 的设定中,\theta 是源数据(训练数据)的唯一表示形式,直接修改 \theta 可能导致模型偏离其训练目标。
- 模型 f 通常是高度非线性的,且 \theta 的维度可能非常高,这使得在测试阶段对 \theta 进行优化既过于敏感又效率低下。
(归一化和参数变换)
为了保证稳定性和效率,作者转而仅更新那些 线性调制 (如缩放和偏移)以及 低维调制 (逐通道操作)的参数。图 4 展示了调制方法的两个步骤:通过统计量进行归一化,以及通过参数进行变换。

(归一化步骤)
归一化通过对输入 x 的均值 \mu 和标准差 \sigma 进行中心化和标准化,得到归一化的特征:
其中,统计量 \mu 和 \sigma 是从数据中估计出来的。
(变换步骤)
变换通过仿射参数(缩放参数 \gamma 和偏移参数 \beta )将归一化的特征 \bar{x} 转换为输出特征:
这里,参数 \gamma 和 \beta 则通过损失函数进行优化。
(实现细节)
为了简化实现,我们 直接利用源模型中的归一化层(如 BatchNorm 或 LayerNorm)。在测试阶段,我们更新这些归一化层的所有层和通道的统计量(\mu, \sigma)以及仿射参数(\gamma, \beta)。
3.3 算法
(初始化)
优化器收集源模型中每个归一化层 l 和通道 k 的仿射变换参数 \{\gamma_{l,k}, \beta_{l,k}\}。其余参数 \theta \setminus \{\gamma_{l,k}, \beta_{l,k}\} 被固定不变。源数据中的归一化统计量 \{\mu_{l,k}, \sigma_{l,k}\} 被丢弃。
(迭代)
每一步都在一批数据上更新归一化统计量和变换参数。在前向传播过程中,逐层估计归一化统计量。在反向传播过程中,通过预测熵的梯度 \nabla H(\hat{y}) 更新变换参数 \gamma, \beta。需要注意的是,变换参数的更新基于当前批次的预测结果,因此它只会影响下一个批次(除非前向传播被重复执行)。此方案每次只需计算一个额外的梯度点,因此为了效率,默认使用这种方法。
(终止)
对于在线自适应,无需终止条件,只要还有测试数据,迭代就会继续。对于离线自适应,模型首先被更新,然后重新进行推理。当然,自适应可以通过多轮迭代继续进行。
4 实验
略
5 总结
Tent 通过 测试时间的熵最小化 减少了在分布偏移数据上的泛化误差。在最小化熵的过程中,模型通过自身的预测反馈进行自我调整。这是一种真正的自监督式自我改进。与那些为从数据中提取更多监督信号而设计的代理任务不同,这种自监督完全由监督任务定义,但仍然显著地减少了误差。然而,由于损坏和其他分布偏移导致的误差依然存在,因此还需要更多的自适应调整。下一步的研究应探索针对更多、更复杂类型的分布偏移,对更通用的参数进行测试时间自适应,并设计更高效和有效的损失函数。