论文 - 《Video Test-Time Adaptation for Action Recognition》
代码 - Github
关键词 - 动作识别、test-time adaptation、视频、CVPR 2023

摘要

研究背景：目前动作识别系统在面对测试数据中未预料到的分布偏移时表现得十分脆弱，尚未有研究证明视频动作识别模型能够针对常见的分布偏移进行测试时自适应（2023年发表的）
本文工作
- 提出了一种专门针对时空模型的方法来解决这一问题，该方法能够在单个视频样本的基础上逐步实现自适应。
- 具体而言，本文的方法采用了一种特征分布对齐技术，将测试集统计量的在线估计与训练统计量对齐。此外，本文的方法进一步增强了同一测试视频样本在时间增强视图上的预测一致性。
实验结果
- 在三个基准动作识别数据集上的评估表明，所提出的技术具有架构无关性，并能够显著提升当前最先进的卷积架构 TANet 和 Video Swin Transformer 的性能。
- 方法在单一分布偏移和更具挑战性的随机分布偏移两种测试场景中，相较于现有的测试时自适应方法均表现出显著的性能优势。

1 引言

视频模态常见的域偏移
- 用于识别机动车或行人交通事件的摄像头可能会记录到罕见的天气状况（如冰雹风暴）。
- 体育动作识别系统可能受到体育场馆观众引发的干扰（如焰火烟雾）的影响。
- 视频处理设置中的细微变化也可能导致数据分布的偏移，例如用于压缩视频流的算法发生变化。
视频 test-time adaptation 意义
- 为图像分类开发的方法并不适合动作识别任务，大多数动作识别应用需要在线运行内存和计算密集型的时间模型，并且要求延迟最小化，同时受限于严格的硬件条件。
- 视频比图像更容易受到分布偏移的影响，例如曝光时间有限引起光照变化导致的噪声水平波动、运动模糊、压缩伪影。
- 如图1展示了一些分布偏移的例子。

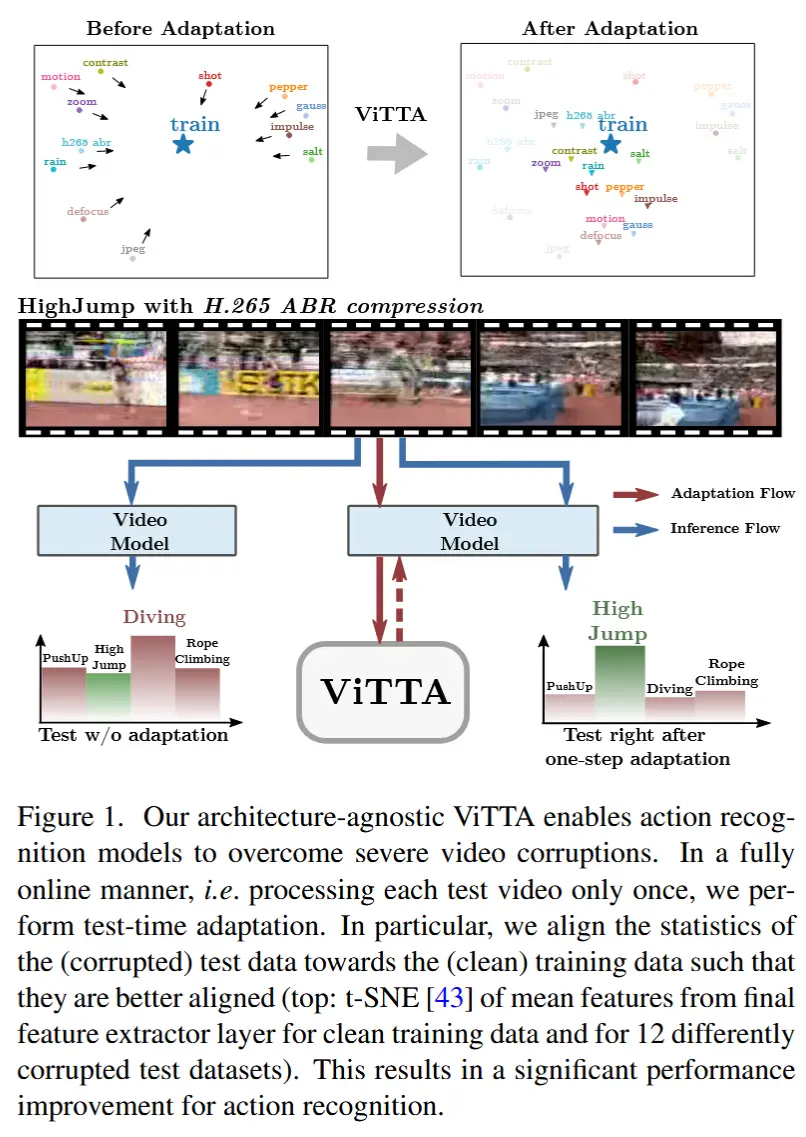
ViTTA
- 首个视频测试时自适应方法。
- 特征对齐：作者采用了 特征对齐（feature alignment），这是一种常见的 TTA 方法，通过 最小化测试数据和训练数据特征分布的统计量差异 来实现对齐。特征对齐不需要对训练过程进行任何修改，并且具有架构无关性。
- EMA：作者通过使用 指数移动平均（exponential moving average, EMA） 来在线估计测试特征统计量，解决了现有特征对齐方法的问题（需要较大的测试批次来准确估计统计量）。
- 重采样视频帧：此外，作者发现尽管视频数据的时间维度带来了挑战，但它也蕴含着潜在的优势。通过时间重采样视频帧创建输入视频的增强视图，从而利用这一优势。两个好处：
  - 1）多个增强视图能够更准确地反映整体视频内容的统计特性。
  - 2）它允许我们在不同视图之间强制预测一致性，从而使自适应更加有效。

2 相关工作

动作识别
- 主要通过基于 CNN 和基于 Transformer 的架构来解决。
  - 基于CNN 的架构通常使用 3D 卷积，例如 C3D [41]、I3D [5]、SlowFast [10] 和 X3D [9]。也有部分工作研究使用结合时间模块的 2D 卷积来减少计算开销，例如 TEINet [27] 和 TANet [29]。
  - 基于 Transformer 的模型也被应用于视频识别任务。ViViT [1] 在空间编码器之上添加了多个时间 Transformer 编码器。Video Swin Transformer [28] 使用时空局部窗口来计算自注意力机制。
- 在本工作中，作者在 TANet 和 Video Swin Transformer 上评估了提出的自适应方法。
视频模型在动作识别中的鲁棒性
- Yi 等人 [53] 和 Schiappa 等人 [35] 对常见的基于卷积和基于 Transformer 的时空架构进行了基准测试，评估其在视频采集和视频处理过程中遇到的多种干扰下的鲁棒性。
- 在本工作中，作者对这两项基准研究中提出的 12 种干扰进行了评估。这些干扰涵盖了各种类型的噪声和数字错误、相机模糊效应、天气条件，以及图像和视频压缩中的质量退化。
测试时自适应
- 旨在以无监督的方式应对测试时遇到的未知分布偏移问题。
- 这些方法可以分为两类：
  - 1）修改训练过程，并引入自监督辅助任务以在测试时适应分布偏移。
  - 2）在不改变训练的情况下适应现成的预训练网络，这类方法通常采用后验正则化。（这一类与本文更相关）
- 尽管在图像领域取得了密集的发展，但针对视频动作识别模型的测试时自适应尚未被证明。

两类测试时自适应相关工作

1）修改训练过程，并引入自监督辅助任务以在测试时适应分布偏移。

Sun 等人 [40] 联合训练网络以完成自监督旋转预测任务 [13] 和图像分类的主要任务。在测试时，他们通过测试样本上的旋转预测辅助任务获得梯度，更新编码器以适应分布外测试数据。

TTT++ [25] 提出了自监督对比学习 [6] 作为辅助目标，并对齐源域和目标域的特征响应。

Gandelsman 等人 [11] 使用基于掩码自动编码器 [15] 的自监督重建任务进行测试时自适应。

2）在不改变训练的情况下适应现成的预训练网络，这类方法通常采用后验正则化。（这一类与本文更相

TENT [44] 在测试时通过最小化输出 softmax 分布的熵来适应预训练网络。

MEMO [57] 提出在测试时通过最小化增强视图上的边际输出分布熵来适应网络。

SHOT [23] 同样使用熵最小化，并在测试时加入信息最大化正则化。

LAME [4] 仅通过拉普拉斯正则化调整网络的输出，并通过凹凸优化程序保证收敛。

T3A [18] 从测试样本生成伪原型并替换在训练集上学习到的分类器。

DUA [30] 和 NORM [36] 仅更新批量归一化层的统计量以实现测试时自适应。

3 Video Test-Time Adaptation (ViTTA)

TTA 场景中提供了一个在视频序列训练集 S 上训练的动作识别多层神经网络 \phi ，以及其最优参数向量 \hat{\theta} ，该参数向量是通过训练得到的。在测试时，网络会暴露于来自测试集 T 的无标签视频，这些视频可能与训练集 S 中的数据分布不同。我们的目标是使 \phi 适应这种分布偏移，以最大化其在测试视频上的性能。

ViTTA 方法流程如图 2 所示。

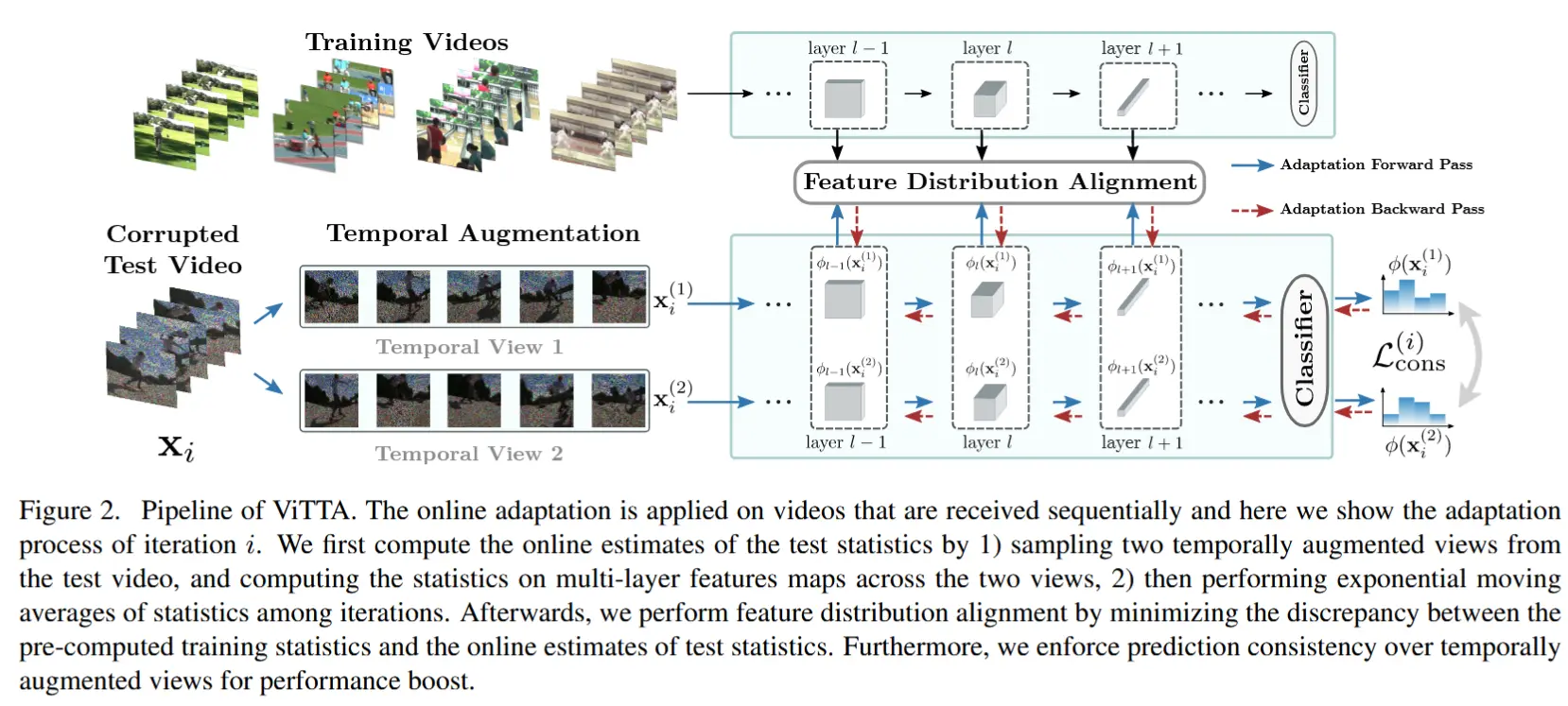
3.1 特征分布对齐

ViTTA 通过对齐训练视频和测试视频的特征图分布来实现自适应。根据最近关于 TTA [30, 36] 的研究，为了对齐分布，需要将特征图的均值和方差进行标准化。

（一些定义）将 网络 \phi 第 l 层的特征图表示为 \phi_l(\mathbf{x}; \theta) ，其中 \theta 是用于计算的参数向量。特征图是一个大小为 (c_l, t_l, h_l, w_l) 的张量，其中 c_l 表示第 l 层的通道数，t_l 、 h_l 和 w_l 分别表示其时间维度和空间维度。特征图的空间-时间范围表示为 V = [1, t_l] \times [1, h_l] \times [1, w_l] ，并将位于体素（voxel） v \in V 处的 c_l 维特征向量表示为 \phi_l(\mathbf{x}; \theta)[v] 。

（特征均值） 对于数据集 D ，第 l 层特征的均值向量可以计算为样本期望：

\mu_l(D; \theta) = \mathbb{E}_{\mathbf{x} \in D \ v \in V} \left[ \phi_l(\mathbf{x}; \theta)[v] \right], \tag{1}

（特征方差）第 l 层特征的方差向量可以通过以下公式获得：

\sigma^2_l(D; \theta) = \mathbb{E}_{\mathbf{x} \in D \ v \in V} \left[ \left( \phi_l(\mathbf{x}; \theta)[v] - \mu_l(D; \theta) \right)^2 \right]. \tag{2}

为了简化公式表达，将训练统计量的符号简化为 \hat{\mu}_l = \mu_l(S; \hat{\theta}) 和 \hat{\sigma}^2_l = \sigma^2_l(S; \hat{\theta}) 。在实验中，预先在训练数据上计算这些统计量。 当训练数据不再可用时，可以使用另一个未标注数据集的统计量替代，前提是该数据集已知来自相似分布。

（对齐损失）总体方法是迭代更新参数向量 \theta ，以将选定层的测试统计量与训练数据计算的统计量对齐。这可以形式化为最小化对齐目标：

L_{\text{align}}(\theta) = \sum_{l \in L} \left( |\mu_l(T; \theta) - \hat{\mu}_l| + |\sigma^2_l(T; \theta) - \hat{\sigma}^2_l| \right), \tag{3}

其中，L 是需要对齐的层集合，|\cdot| 表示向量的 l_1 范数，T 表示测试集。

通过训练网络来对齐分布的方法在本质上不同于基于特征对齐的 TTA 技术，后者仅调整归一化层中累积的运行统计量，因此并未真正实现测试时的学习。并且 ViTTA 更新整个参数向量的事实使本文的方法区别于仅更新仿射变换层参数的现有算法，从而在自适应过程中赋予其更大的灵活性（虽然调整整个参数，但是实验4.4.5证明适应速度很快）。

作者还发现，对于 TANet 和 Video Swin Transformer ，通过对四个块中最后两个块输出的特征分布进行对齐，可以获得最佳性能。因此将 L 设置为包含这两个块中的层。

3.2 在线自适应

优化公式 (3) 中的目标需要迭代估计测试集的统计量，这是一个耗时的过程，而在典型的在线视频识别系统中，通常要求以最小延迟处理数据流，因此这种操作是不可行的。（需要优化公式 (3) 对齐目标）

假设测试数据以视频序列的形式呈现给自适应算法，记为 \mathbf{x}_i，其中 i 是测试视频的索引。针对序列中的每个元素执行一次自适应步骤。单个测试样本计算出的特征统计量并不能代表整个测试集的特征分布，因此在对齐分布时不能仅依赖它们。

（更新后的均值方差公式） 因此，通过连续测试视频上计算的统计量的指数移动平均值 EMA 来近似测试集的统计量，并将其用于对齐过程。将第 i 次迭代中的均值和方差估计定义为：

\mu_l^{(i)}(\theta) = \alpha \cdot \mu_l(\mathbf{x}_i; \theta) + (1 - \alpha) \cdot \mu_l^{(i-1)}(\theta), \tag{4}

\sigma_l^2{}^{(i)}(\theta) = \alpha \cdot \sigma_l^2(\mathbf{x}_i; \theta) + (1 - \alpha) \cdot \sigma_l^2{}^{(i-1)}(\theta). \tag{5}

其中，1 - \alpha 是动量项，通常设置为一个常见的选择值 0.9（即 \alpha = 0.1 ）。

（新的对齐损失） 为了适应在线自适应，在第 i 次对齐迭代中，公式 (3) 中的目标被近似为：

\mathcal{L}_{\text{align}}^{(i)}(\theta) = \sum_{l \in L} \left| \mu_l^{(i)}(\theta) - \hat{\mu}_l \right| + \left| \sigma_l^2{}^{(i)}(\theta) - \hat{\sigma}_l^2 \right|. \tag{6}

这种方法同时减少了估计值的方差，并让网络不断适应不断变化的测试数据分布。

3.3 时间增强

（时间增强视图的均值方差） 为了进一步提高方法的效率，作者利用数据的时间特性，并对 同一视频创建 M 个时间增强视图。将输入视频 \mathbf{x}_i 的时间增强视图表示为 \mathbf{x}_i^{(m)}，其中 1 \leq m \leq M 。计算视频 \mathbf{x}_i 在 M 个视图上的均值和方差向量，以提高单个视频统计量的准确性：

\mu_l(\mathbf{x}_i; \theta) = \mathbb{E}_{m \in M} \left[ \phi_l(\mathbf{x}_i^{(m)}; \theta)[v] \right], \tag{7}

\sigma^2_l(\mathbf{x}_i; \theta) = \mathbb{E}_{m \in M} \left[ \left( \phi_l(\mathbf{x}_i^{(m)}; \theta)[v] - \mu_l(\mathbf{x}_i; \theta) \right)^2 \right]. \tag{8}

回顾一下，\mu_l(\mathbf{x}_i; \theta) 和 \sigma^2_l(\mathbf{x}_i; \theta) 被用于公式 (11) 和 (12) 中，以在第 i 次迭代中计算均值和方差估计。

附录公式（11）和（12）

\mu_l^{(i)}(\theta) = \alpha \cdot \mu_l(\mathbf{x}_i; \theta) + (1 - \alpha) \cdot \mu_l^{(i-1)}(\theta), \tag{11}

\sigma_l^2{}^{(i)}(\theta) = \alpha \cdot \sigma_l^2(\mathbf{x}_i; \theta) + (1 - \alpha) \cdot \sigma_l^2{}^{(i-1)}(\theta). \tag{12}

（一致性损失）此外，作者强制要求 M 个视图之间的预测一致性。通过平均网络对输入视图预测的类别概率来建立伪标签： y(\mathbf{x}) = \frac{1}{M} \sum_{m=1}^M \phi(\mathbf{x}_i^{(m)}; \theta) ，并定义第 i 次迭代的一致性目标为：

\mathcal{L}_{\text{cons}}^{(i)}(\theta) = \sum_{m=1}^M \left| \phi(\mathbf{x}_i^{(m)}; \theta) - y(\mathbf{x}) \right|. \tag{9}

（总梯度更新参数） 在第 ( i ) 次对齐迭代中，根据以下梯度更新网络参数：

\min_\theta \mathcal{L}_{\text{align}}^{(i)}(\theta) + \lambda \cdot \mathcal{L}_{\text{cons}}^{(i)}(\theta), \tag{10}

其中，\lambda 是设置为 0.1 的系数。在消融研究中，表明设置 ( M = 2 ) 就足以带来显著的性能提升（见第 4.4.3 节），并且均匀等距重采样输入视频可以获得最佳结果（见第 4.4.4 节）。

4 实验

4.1 实验设定

数据集
- UCF101 ：包含从 YouTube 收集的 13,320 个视频，涵盖 101 个动作类别。本文在分割 1 上进行评估，该分割包含 9,537 个训练视频和 3,783 个验证视频。
- Something-something v2（SSv2）：这是一个大规模的动作数据集，包含 168,000 个训练视频和 24,000 个验证视频，共涉及 174 个类别。
- Kinetics 400（K400）：这是动作识别任务中最流行的基准数据集，包含约 240,000 个训练视频和 20,000 个验证视频，共涉及 400 个类别。
干扰类别
- 作者基于 [35, 53] 中提出的 12 种干扰类型来评估时空模型的鲁棒性。
- 12 种干扰包括：高斯噪声、椒盐噪声（Pepper noise）、盐噪声（Salt noise）、脉冲噪声（Shot noise）、缩放模糊（Zoom blur）、冲击噪声（Impulse noise）、失焦模糊（Defocus blur）、运动模糊（Motion blur）、JPEG 压缩、对比度变化（Contrast）、雨天效果（Rain）、H.265 自适应比特率压缩（H.265 ABR compression）
- 涵盖了各种类型的噪声和数字错误、相机模糊效应、天气条件，以及图像和视频压缩中的质量退化
- 由于鲁棒性分析表明严重程度与性能下降之间存在近似线性相关性，因此作者在最严重的第 5 级干扰上进行评估。
实验细节
- 模型：基于 ResNet50 [16] 的 TANet [29] 和基于 Swin-B [26] 的 Video Swin Transformer [28]。
- 对最后两个块中归一化层的特征进行分布对齐。
- 在所有数据集上的评估中，将批处理大小设置为 1，并且每个视频仅适应一次。
- 遵循在线测试时自适应的常见做法，在适应样本后立即进行推理，并报告所有样本的累积准确率。
- 对于时间增强（temporal augmentation），采用均匀等距采样和随机空间裁剪的方法。

4.2 sota 对比

基线方法
- SourceOnly ：直接使用在训练数据上训练的模型生成预测结果，不进行任何自适应。
- NORM [36] ：通过调整批量归一化层的统计量以适配测试数据。
- DUA [30] ：在线调整批量归一化层。
- TENT [44] ：通过最小化测试预测的熵来学习特征图的仿射变换。
- SHOT (online) [23] ：最大化预测类别分布的批处理熵，同时最小化单个预测的熵。
- T3A [17] ：从测试数据中构建伪原型。

4.2.1 单一分布偏移下的评估

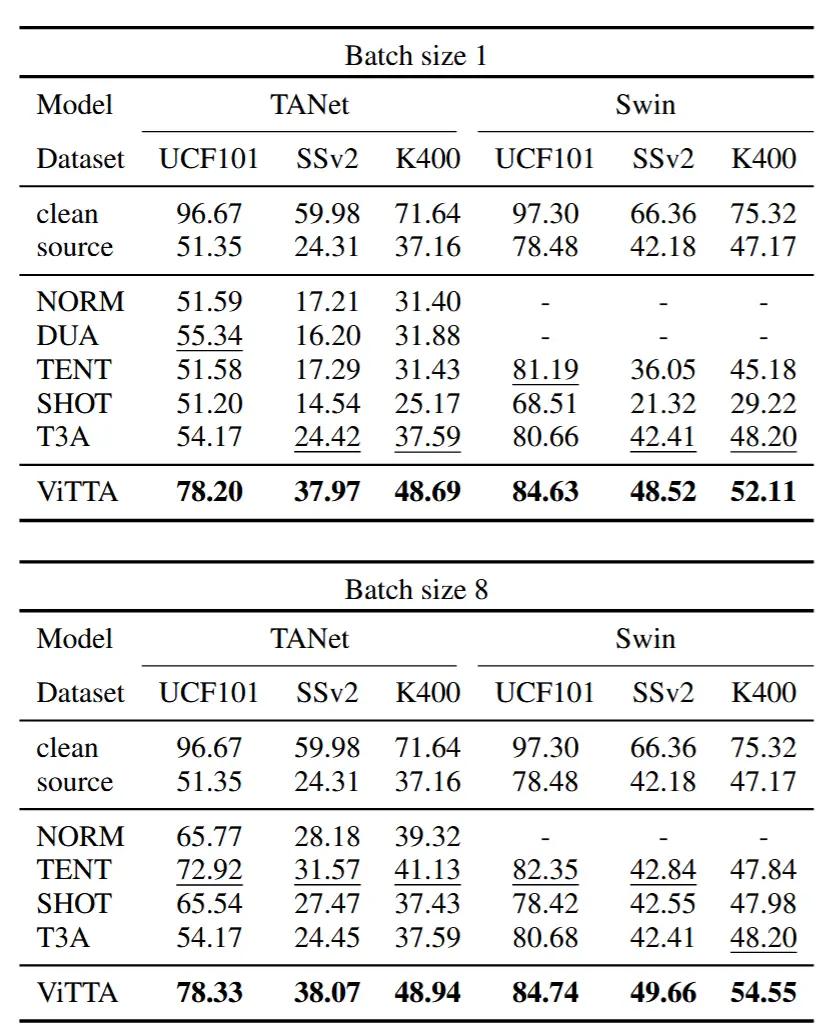
表 1
- 在三个数据集所有干扰类型上自适应的平均分类准确率，Video Swin Transformer。
- clean 和 sourceonly 对比：干扰显著降低了性能。
- 批处理设置为8：基线方法性能得到增强，但是ViTTA仍然领先。（由于 ViTTA 以在线方式累积测试统计量，而不是依赖于数据批次中的统计量，因此它不需要较大的批处理大小即可实现良好的自适应性能）

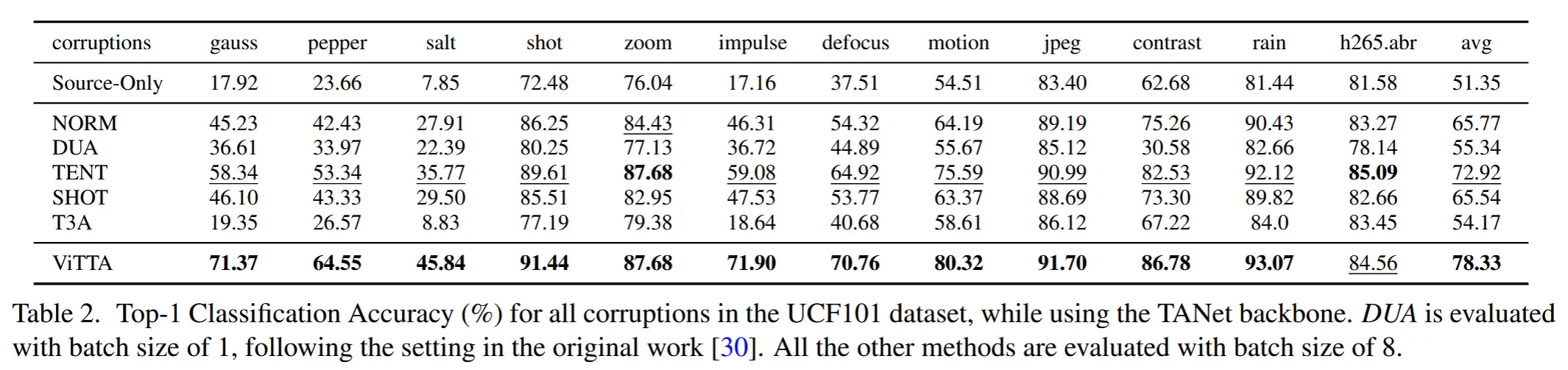
表 2
- TANet 在 UCF101 数据集上针对所有 12 种干扰类型的自适应结果。
- 对于大多数干扰类型，ViTTA 相较于基线方法具有显著的优势。

4.3.2 随机分布偏移下的评估

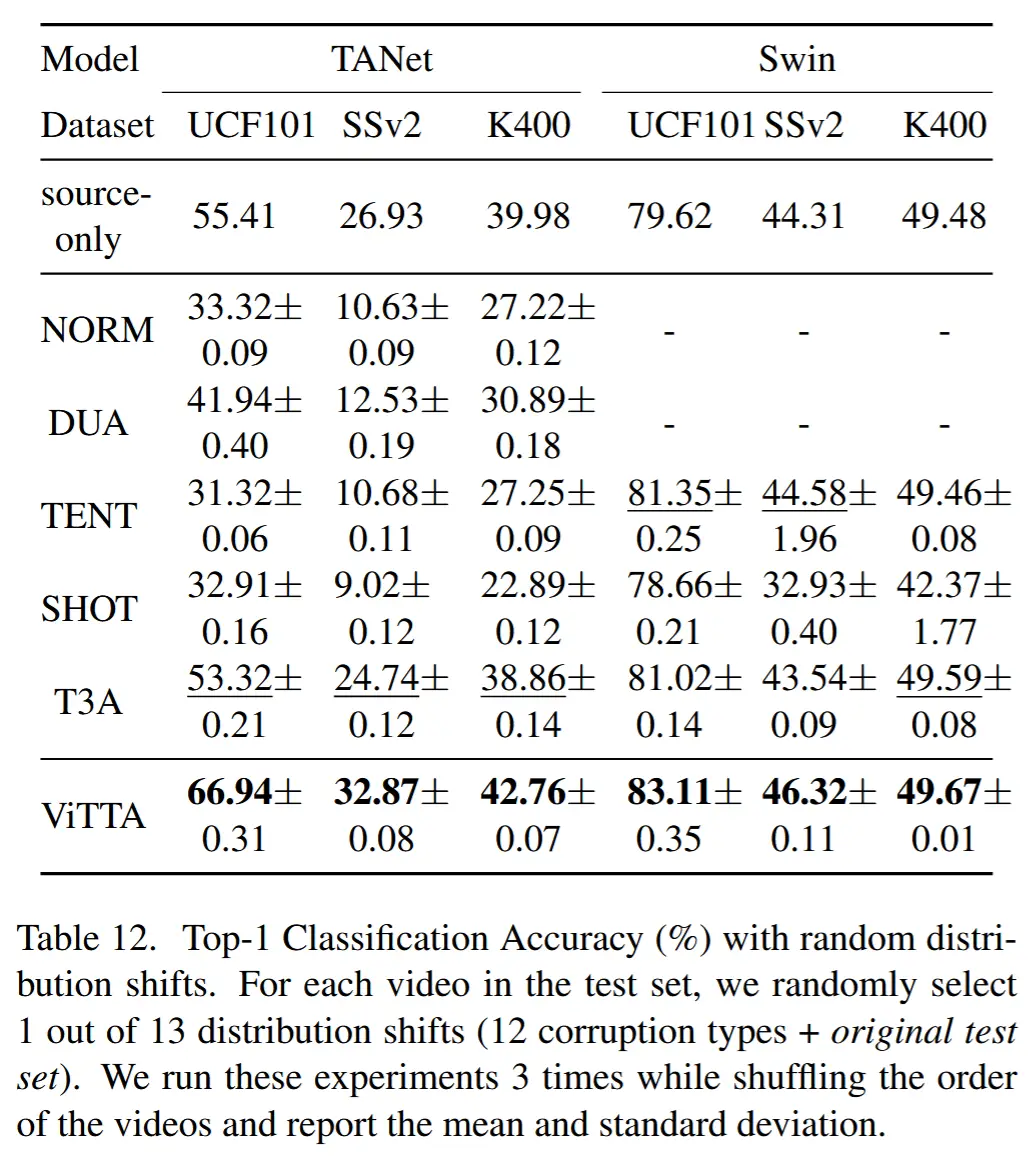
表12
- 假设接收到的每个视频都具有随机类型的分布偏移
- 对于许多数据集和骨干架构的组合，基线方法会降低未自适应模型的性能。
- 而 ViTTA 在所有数据集和架构上始终能够提升性能。归因于：在多个自适应迭代中聚合统计量的技术，这减少了从具有不同干扰的数据批次计算出的梯度的波动。

4.3 消融研究

4.3.1 特征图对齐的选择

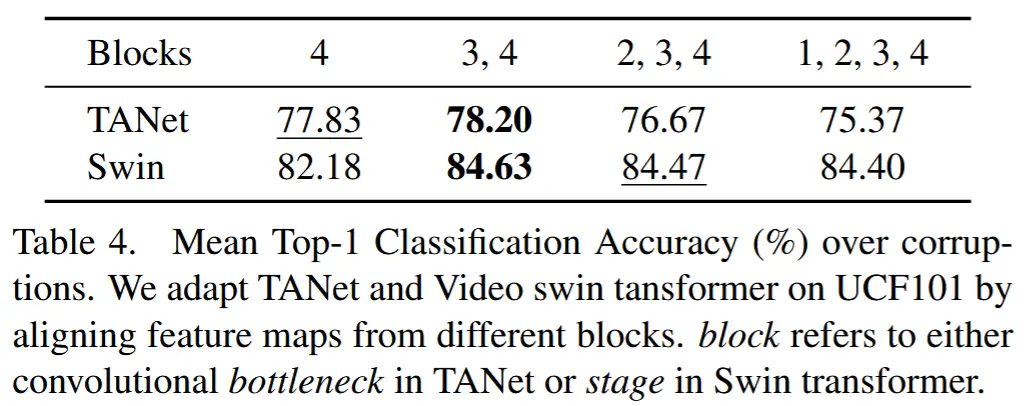
表4
- 实验方法：将 TANet 和 Video Swin Transformer 适应到受干扰的 UCF101 验证集上，尝试对不同块组合输出的特征图进行对齐。（这里的“块”指的是 TANet 中的卷积瓶颈层或 Swin Transformer 中的阶段。）
- 结果表明，一种折中的方法效果最佳：对最后两块生成的特征图进行对齐。
- 归因：
  - 1）在自适应过程中保留过多自由度可能会导致匹配最后一层的分布，但无法传递特征语义。
  - 2）在架构的较低层中保留一定程度的自由度可能是必要的，以便网络能够学习将受干扰数据的外观映射到计算图中更深的层的特征空间，而这些特征空间是在未受干扰的训练数据上学习的。

4.3.2 归一化层中存储的统计量

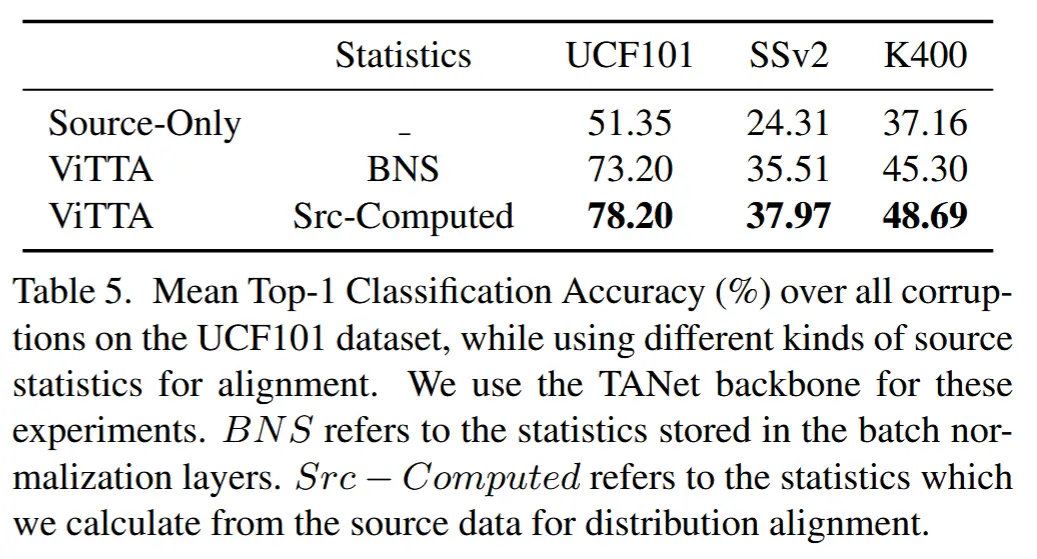
表5
- 前情介绍：特征分布对齐时需要在训练数据上计算的特征均值和方差。当训练数据不再可用时，这些统计量可以在具有相似分布的其他数据上计算。对于包含 Batch Normalization 层的架构，使用在训练期间累积的运行均值和方差是一种方便的替代方案。
- 实验目的：为了研究替代方案的不准确性如何影响性能。
- 实验方法：将使用替代方案的结果与使用训练集上计算的统计量的结果进行了比较。
- 结果表明，依赖运行均值和方差的性能略低于从头计算统计量的性能，但仍高于基线方法的性能。

4.3.3 视图数量与预测一致性

表6
- 实验目的：验证时间增强视图和强制预测一致性的有效性。
- 实验结果：
  - 强制预测一致性：当不使用预测一致性时，采样两个时间增强视图（77.46%）相较于仅使用一个视图（75.57%）带来了约 2% 的性能提升。
  - 增强时间视图：随着视图增加性能逐渐提升。

4.3.4 时间采样策略

表 7
- 对于片段选择：均匀采样和密集采样；对于帧采样：随机采样和等距采样；除此以外还可以完全随机采样。
- 结果表明，ViTTA 方法能够很好地泛化到不同类型的帧采样策略，其中，均匀等距采样 表现最佳。

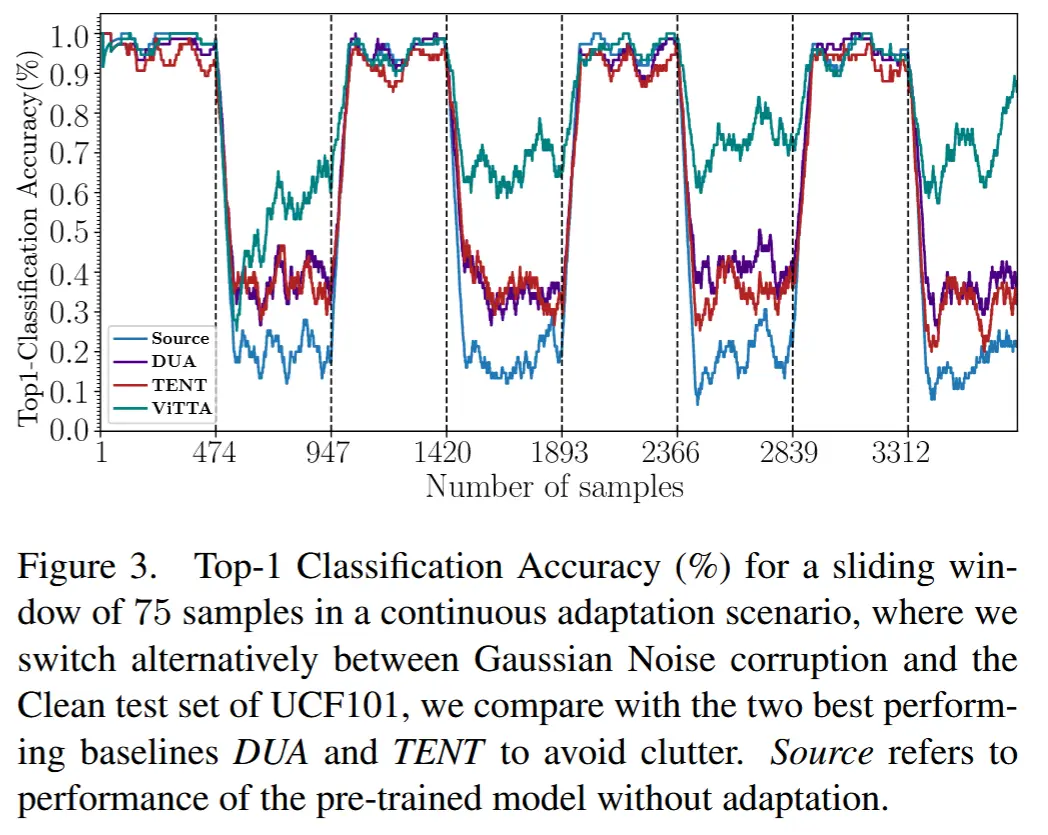
4.3.5 持续自适应

图3
- 实验目的：检验了这些方法重新适应未受干扰数据的能力。
- 实验方法：每隔约 500 个测试视频周期性地开启和关闭干扰，使用高斯噪声作为干扰技术。
- 实验结果：在受干扰的阶段，ViTTA 始终表现最佳，并且在未受干扰阶段仍能快速恢复性能。

5 总结

我们解决了视频动作识别模型在测试时自适应以应对常见干扰的问题。我们提出了一种针对视频设计的方法，该方法将训练统计量与目标统计量的在线估计对齐。为了进一步提升性能，我们强制对视频样本的时间增强视图进行预测一致性。我们在三个动作识别数据集上对现有的 TTA 技术进行了基准测试，涵盖了 12 种常见的图像和视频特定干扰。我们提出的 ViTTA 方法在单个干扰和更具挑战性的随机干扰场景的评估中均表现出色。此外，面对分布偏移的周期性变化，它展现了快速的适应性能恢复能力。

论文笔记《Video Test-Time Adaptation for Action Recognition》

摘要