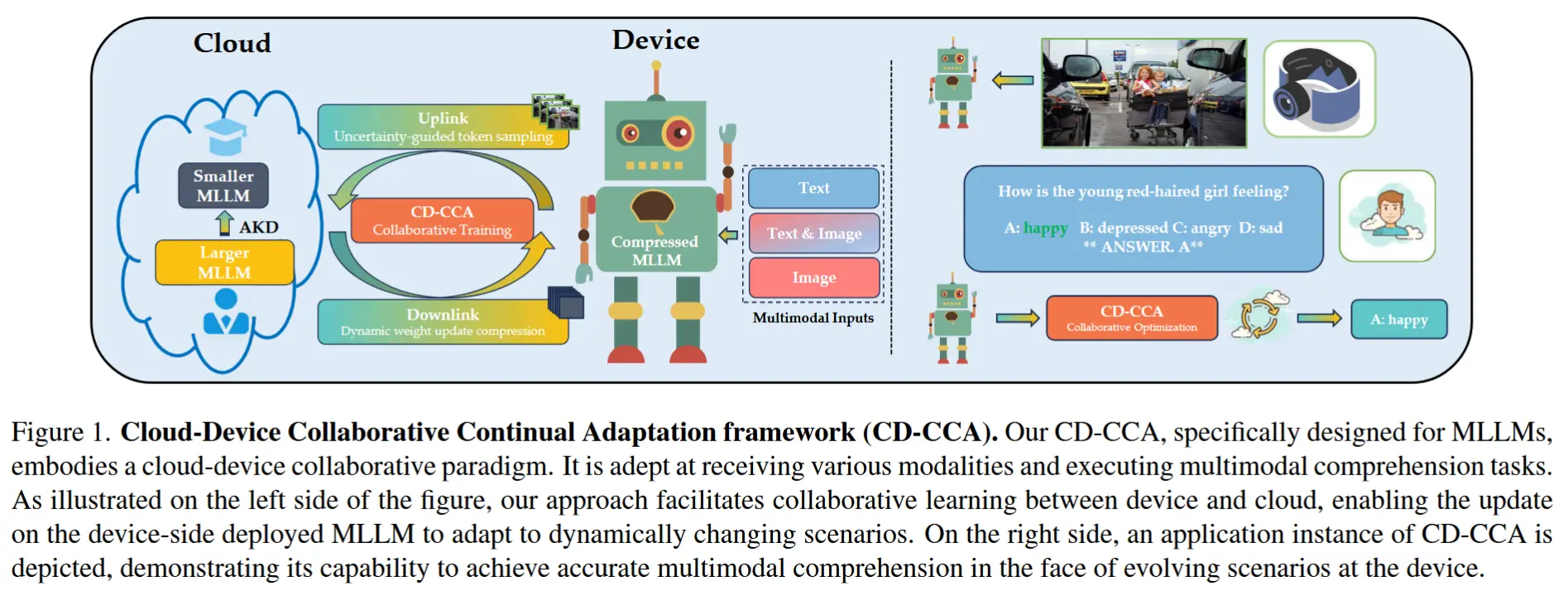
论文笔记《Towards Robust and Efficient Cloud-Edge Elastic Model Adaptation...》

论文笔记《Towards Robust and Efficient Cloud-Edge Elastic Model Adaptation...》

Administrator 20 2025-03-24

摘要

  • 研究背景
    • 传统的深度学习范式在服务器上训练一个深度模型，然后部署到边缘设备。通常情况下，部署之后的模型是固定的，然而在现实场景中，测试环境可能会动态变化（即分布偏移），导致性能下降。
  • 挑战
    • 1）边缘模型的计算能力有限，可能仅支持前向传播；
    • 2）在延迟敏感的场景中，云与边缘设备之间的数据传输预算受到限制。
  • 解决办法
    • 本文提出了一种云边弹性模型适应（Cloud-Edge Elastic Model Adaptation, CEMA）范式，在该范式中，边缘模型只需执行前向传播，并且可以在线适应。
    • 在CEMA中，为了减轻通信负担，设计了两个标准来排除无需上传到云端的样本，即动态不可靠样本和低信息量样本的排除。基于上传的样本，作者通过从更强的基础模型蒸馏知识并结合样本回放策略，更新和分发归一化层的仿射 (affine) 参数。
  • 实验结果
    • 在ImageNet-C数据集上，CEMA相较于现有最先进方法（SOTAs）减少了60%的通信成本。

1 介绍

  • 分布偏移
    • 在现实世界的边缘设备中，环境可能会动态变化，测试样本的分布也与训练样本不同。
    • 这种分布偏移通常由自然变化或损坏引起，例如光照变化和传感器退化。
    • 在这种情况下，模型可能会表现出显著的性能下降。
  • 常见解决办法
    • 1）离线泛化方法在云端执行，然后将更新后的模型分发到边缘设备。具体而言，无监督域适应（domain adaptation）方法以离线方式对收集的测试数据进行模型适应。域泛化方法在训练时预先预测可能的测试偏移，其中可能的偏移可以通过元学习方案（meta-learning scheme）模拟。然而，由于在训练时很难预先预测所有未知的偏移，这些方法可能会导致性能不佳。
    • 2）在线泛化方法通过使用测试数据直接调整模型来学习偏移。最近，测试时训练（test-time training, TTT） 和 完全测试时适应（fully test-time adaptation, TTA） 方法被提出，以在线方式将模型适应到测试域，这在实际应用中更加实用。然而，它们可能需要执行反向传播，计算量较大，这对于资源受限的边缘设备来说可能是无法承受的。

  • 利用云端更新并同步
    • 基本思想：将测试样本上传到云端，在云端完成前向和后向传播并更新参数，之后同步边缘端模型。
    • 挑战：
      • 1）云端与边缘之间的数据通信负担可能很重。
      • 2）如何利用基础模型提升边缘模型在分布偏移测试数据上的性能仍是一个开放性问题。

  • 本文工作-CEMA范式
    • 如图1所示，将所有适应工作负载委托给云端，因此边缘设备仅需执行普通的推理任务。
    • 三个核心点
      • 为了减少通信开销，通过以下方式排除两类样本上传到云端：1）通过动态熵阈值方案识别出的高熵不可靠样本；2）通过固定阈值方案识别出的低熵低信息量样本。
      • 为了利用基础模型中的丰富知识，通过知识蒸馏引导边缘模型进行适应。
      • 为提高上传样本的数据利用效率，设计了一个回放缓冲区来存储和重用这些样本。
    • 通过这种方式，CEMA实现了比普通适应方法更优的性能。
paper17-1.webp

2 通信高效的云边模型适应

2.1 面向鲁棒性与通信增强的高效适应

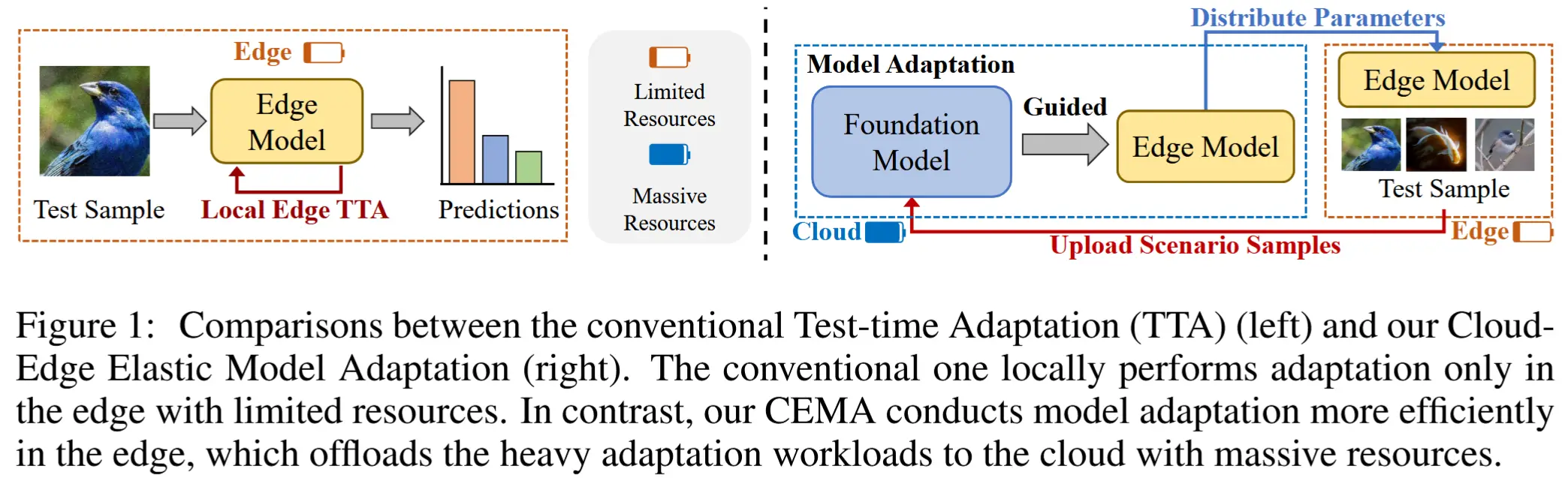
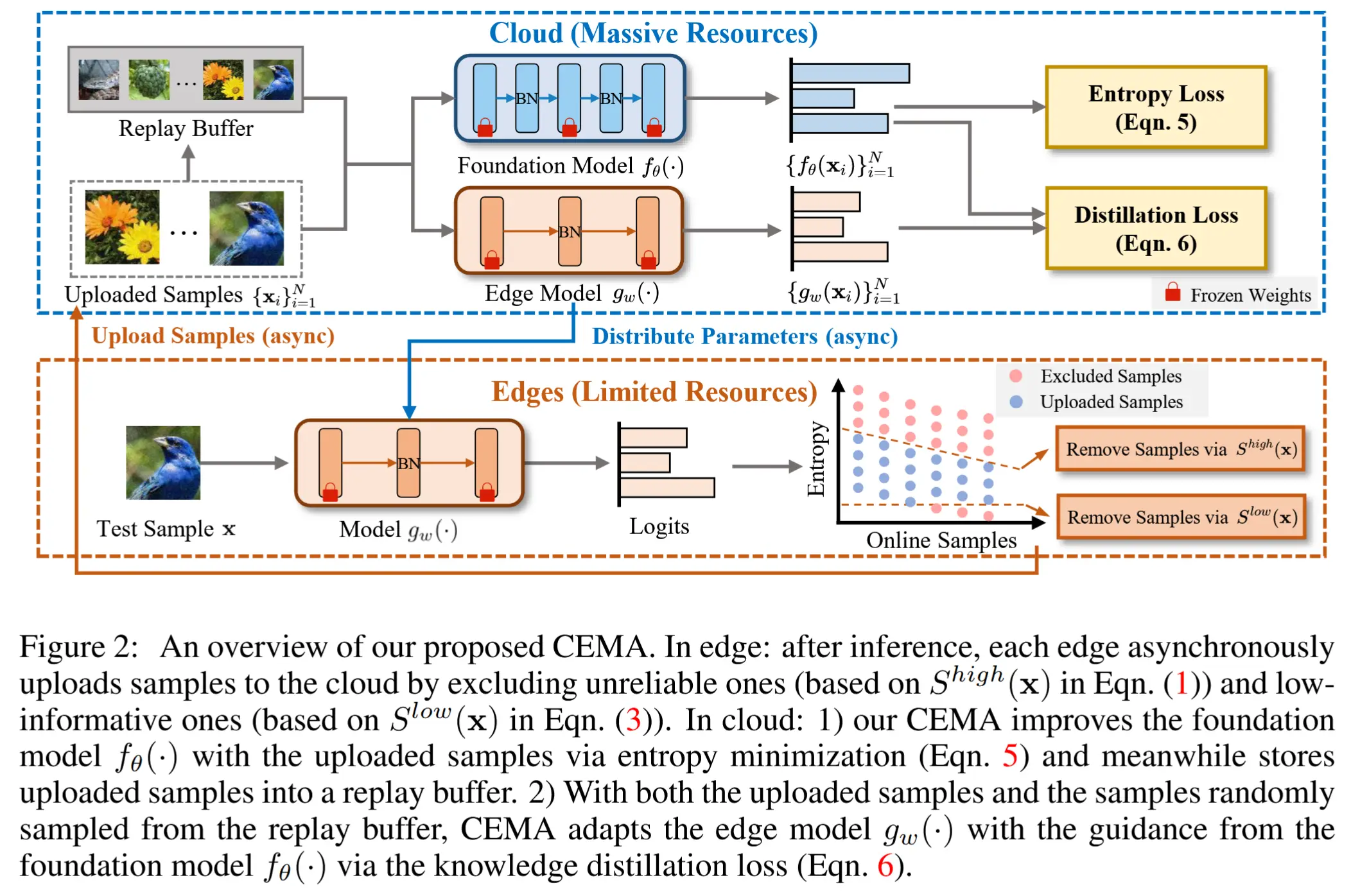
  • CEMA 范式流程如图2所示
    • 边缘设备仅需执行普通的模型推理，而其余的适应工作负载则被卸载到云端。
    • CEMA根据所提出的基于熵的准则，选择性地上传部分样本到云端进行适应。
    • 一旦云端的适应过程完成，边缘模型将从云端更新其参数，并对下一个到来的测试样本进行推理。
      • 具体而言，CEMA 试图利用一个能力更强、参数更多的基础模型 ​f_\theta(·) 来引导边缘模型进行适应。
      • 该基础模型无需访问训练数据，并通过无监督的熵最小化进行更新。
      • 为了最大化适应过程中的数据利用率，作者设计了一个回放缓冲区来存储上传的样本。当通过知识蒸馏从基础模型向边缘模型传递知识时，同时利用新上传的样本和回放缓冲区中的样本。
paper17-2.webp

  • 边缘和云端涉及的伪代码分别展示在算法1和算法2中。
paper17-3.webp

2.2 边缘端通信成本降低的样本过滤

  • 基于熵的模型适应方法相关工作

    • Wang等人（2021）最近的一项研究提出了一种模型适应方法，通过对一批测试样本进行熵最小化来实现适应。
    • 熵最小化通过对数据分布中高密度区域的决策进行惩罚，从而提高对不同类别的分类准确性（Grandvalet & Bengio, 2004），这已被证明是领域适应中的关键约束条件
    • Niu等人（2022）表明，在使用熵最小化时，高熵样本会对适应性能产生不利影响。 原因可能是模型在没有标签的情况下通过熵最小化利用测试样本进行适应，这在处理高熵样本时引入了相当大的不确定性。
    • 然而，这种方法仅基于静态且预定义的阈值来过滤测试样本，存在两个局限性：
      • 1）样本的熵通常会随着适应过程的推进而降低，因此只有部分负面影响较大的样本能够被排除。
      • 2）它忽略了使用极低熵样本进行适应是没有必要的这一事实。

  • 针对局限性两点改进

    • 1）通过根据当前样本的熵动态调整阈值，自适应地排除不可靠的（高熵）样本；
    • 2）排除低信息量的（低熵）样本。
    • 为此，作者设计了一个二元评分 ​S(x) 来指示样本 x 是否应被上传，仅上传评分为 ​S(x)=1 的测试样本，并丢弃评分为 ​S(x)=0 的样本。

  1. 对不可靠样本进行动态鉴定

设 ​1_{\{·\}}(·) 表示指示函数。利用一个熵阈值 ​E_{max} 来过滤掉高熵测试样本，如下所示：

S^{high}(x) = 1_{\{E(x;w)<E_{max}\}}(x), \tag{1}

其中，​E(x;w) 表示样本 x 的预测 ​g_w(x) 的熵。由于 CEMA 通过熵最小化进行适应，测试样本的熵可能会逐渐降低。因此，固定的阈值 ​E_{max} 在适应过程中会逐步排除越来越少的样本。为了验证这一点，作者进行了一项实证研究，揭示了在适应过程的不同阶段中，熵大于固定 ​E_{max} 的测试样本的比例。如图3所示，在最后阶段，过滤掉的样本数量（用红色条表示）比初始阶段要少，这是因为随着适应的进行，预测变得更加确定。

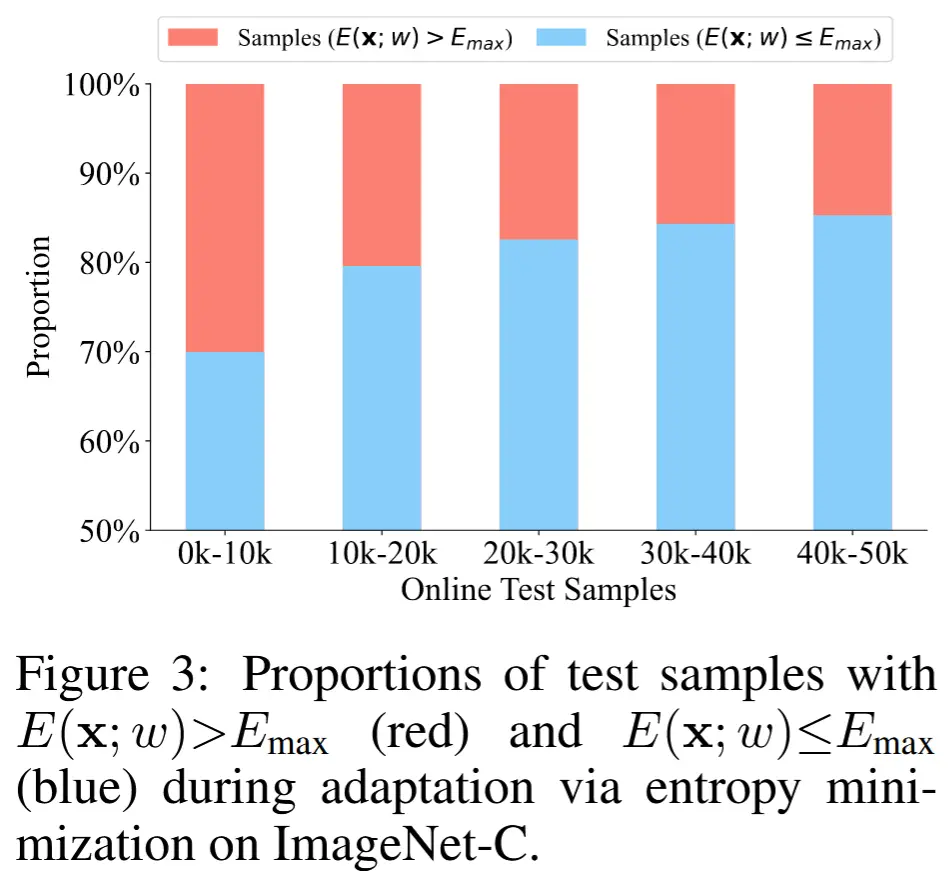
paper17-4.webp

基于上述实证研究，通过动态降低 ​E_{max}，可以过滤掉更多的高熵样本。为此，作者试图根据每次适应批次后测试样本的平均熵来降低 ​E_{max}。具体而言，在第 t 个适应批次中，熵阈值 ​E_{max}^t 可以通过以下公式计算：

E_{max}^t \leftarrow \lambda × E^{t-1}_{max} × \frac {E^t_{avg}} {E^{t-1}_{avg}}, \tag{2}

其中，​E_{avg}^t 表示过去 t 个批次中所有测试样本的平均熵，λ 是一个超参数。注意，​E_{avg}^0 可以从第一批测试样本中获得。通过这种方式，排除更多不可靠样本的上传，从而提高通信效率。


  1. 对低信息量样本的识别

除了高熵样本外，熵极低的测试样本对于适应也是不必要的。因为这些样本在最小化熵损失时仅贡献了可忽略不计的梯度。 按照类似的方案，采用一个阈值 ​E_{min} 来丢弃熵低于阈值的样本。

注意，​E_{min} 没有采用动态变化的策略，因为决定样本是否贡献可忽略梯度的阈值并不依赖于当前测试样本的平均熵。形式上，​S^{low}(x) 可以表示为：

S^{low}(x) = 1_{\{E(x;w) > E_{min}\}}(x), \tag{3}

需要注意的是，边缘模型仅需进行一次常规的前向传播，而无需反向传播或梯度下降。一旦边缘模型对测试样本做出预测，它会通过后台线程异步上传评分为 ​S(x)=1 的样本到云端（非阻塞）。


2.3 基于回放的知识蒸馏用于云端适应

  • 回放缓冲区的原因
    • 普通的蒸馏训练需要大量的样本，而CEMA在边缘端排除了不可靠和低信息量的样本，可访问的测试样本数量有限。
  • 在每次蒸馏步骤中，首先通过无监督熵最小化的方式，在上传的样本上以无监督方式更新基础模型 ​f_\theta(⋅)。通过这一适应过程，基础模型获得了当前测试数据的额外知识。随后，通过基础模型指导的知识蒸馏，在上传的样本和回放缓冲区中的样本上共同提升边缘模型 ​g_w(⋅)。

  1. 基础模型适应的熵最小化

在接收到一批上传的测试样本 ​\hat{X} = \{x_i\}_{i=1}^N 后，首先将其放入回放缓冲区 ​B = B \cup \hat{X} （先进先出策略）。随后，基于批次 ​\hat{X} 更新基础模型（使用批次进行适应不仅避免了平凡解，还提高了云服务器中的并行效率）。形式上，通过最小化加权熵损失 ​L_{\text{ENT}}(f_\theta(x)) 来适应 ​f_\theta(\cdot) ：

\min_{\tilde{\theta}} H(\mathbf{x}) \sum_{y \in \mathcal{C}} f_{\theta}(y | \mathbf{x}) \log f_{\theta}(y | \mathbf{x}), \tag{5}

其中，​H(x) = 1/\exp(E(x; \theta) - E_{\text{max}}) 和 C 表示模型的输出空间。方程（5）是作者按照 （Niu et al.， 2022） 优化了由 H（x） 加权的损失，试图鼓励模型在适应过程中关注低熵测试样本。在反向传播过程中，需要注意的是梯度不会通过 H(x) 进行传播。

为了实现高效的适应，CEMA 仅更新归一化层的仿射参数 ​\tilde{\theta} \in \theta ，而保持其余层的参数固定。这种模型更新策略具有以下三个优势：

1）该策略高效，因为它需要更少的内存占用和计算资源。

2）与将所有参数分发到边缘设备相比，CEMA只需传输 Batch Normalization 参数，从而降低了下载开销。

3）由于大多数参数保持不变，模型可能保留先前的知识，从而带来更好的适应稳定性和性能。


  1. 利用回放缓冲区进行知识蒸馏以适应边缘模型

在上传的样本 ​\hat{X} 和从回放缓冲区 ​B 中随机采样的一组测试样本上适应边缘模型。具体而言，通过 Kullback-Leibler（KL）散度 ​L_{\text{KL}} 对齐基础模型 ​f_\theta(\cdot) 和边缘模型 ​g_w(\cdot) 的预测结果。此外，CEMA 通过交叉熵损失 ​L_{\text{CE}} 适应 ​g_w(\cdot) ，其中伪标签 ​\hat{y} 由基础模型生成。注意，​\hat{y} 可以通过公式 ​\hat{y} = \arg\max_{y \in C}(f_\theta(y|x)) 计算得到。形式上，通过结合熵最小化和知识蒸馏来优化 ​g_w(\cdot)，如下所示：

\min_{\tilde{w}} H(\mathbf{x}) \left[ \alpha \mathcal{L}_{\text{KL}}(g_w(\mathbf{x}), f_\theta(\mathbf{x})) + \beta \mathcal{L}_{\text{CE}}(g_w(\mathbf{x}), \hat{y}) + \mathcal{L}_{\text{ENT}}(g_w(\mathbf{x})) \right], \tag{6}

CEMA 使用 KL 散度 对齐基础模型和边缘模型的预测分布，使用交叉熵损失对齐决策边界。这两种损失使边缘模型以互补的方式从基础模型中学习知识。

在边缘模型适应过程中，仍然仅更新归一化层的仿射参数 ​\hat{w} \in w 。


3 实验

  • 数据集
    • ImageNet-C：分布偏移数据集，通过4大类（噪声、模糊、天气、数字化）共15种不同的损坏类型应用于ImageNet验证集。每种损坏有5个严重程度级别（1到5），级别越高表示分布偏移越严重。
    • ImageNet-R ：包含30,000张图像，涵盖200个ImageNet类别的各种艺术渲染图像，用于进一步验证CEMA。
  • 模型
    • 基础模型 ：ResNet-101
    • 边缘模型 ：ResNet-18
  • 对比方法
    • BN Adaptation (Schneider et al., 2020)、ONDA (Mancini et al., 2018)、LAME (Boudiaf et al., 2022)、Pseudo Label (PL) (Lee et al., 2013)、Tent (Wang et al., 2021)、CoTTA (Wang et al., 2022)、ETA (Niu et al., 2022)

3.1 在ImageNet-C上的性能对比

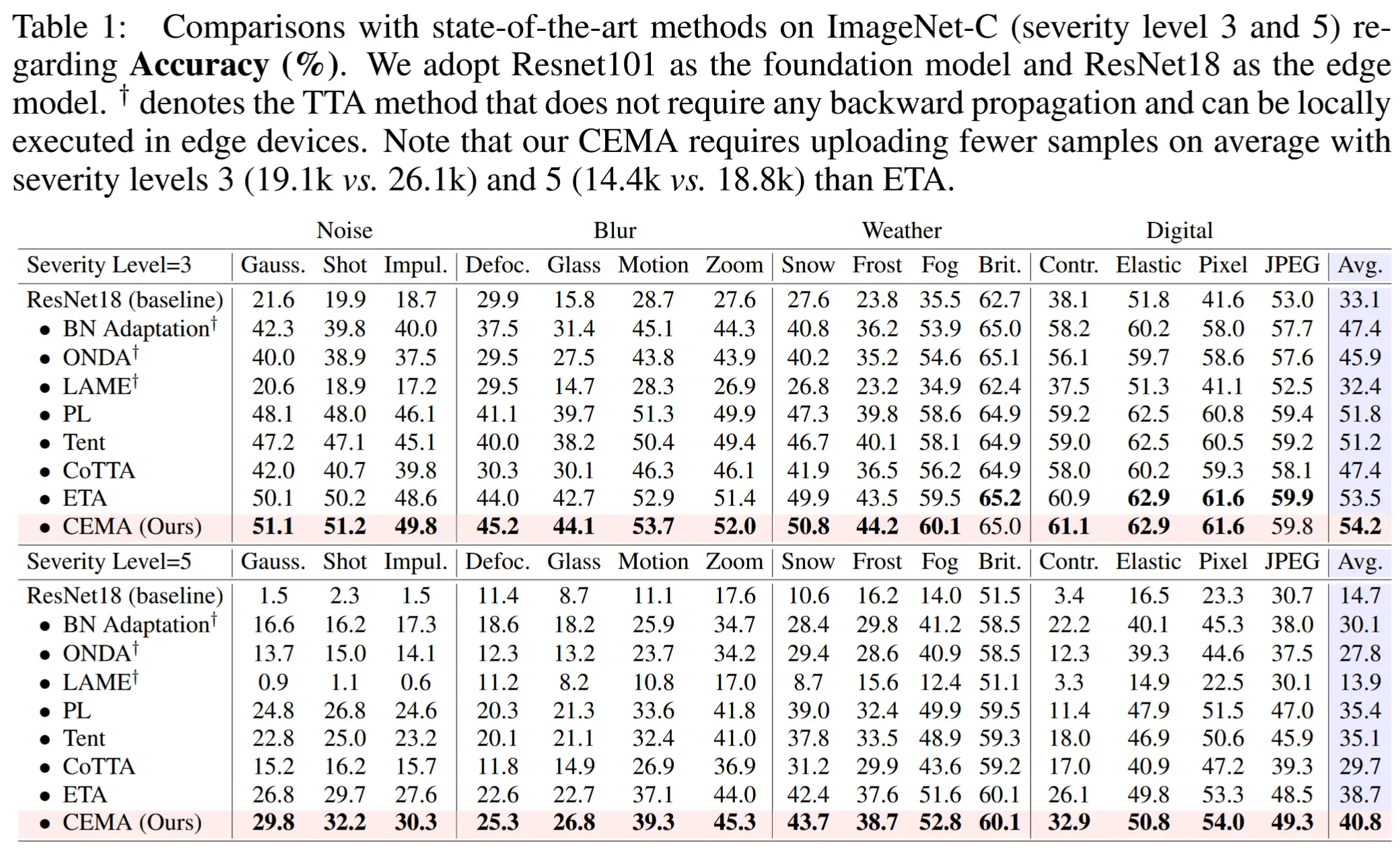
  • 在 ImageNet-C（严重性级别 3 和 5）上与最先进的方法在准确性方面的比较
    • 如表1所示
    • 结果：CEMA在15种损坏类型中的大多数情况下达到了最高准确率，并取得了最佳平均准确率
paper17-5.webp

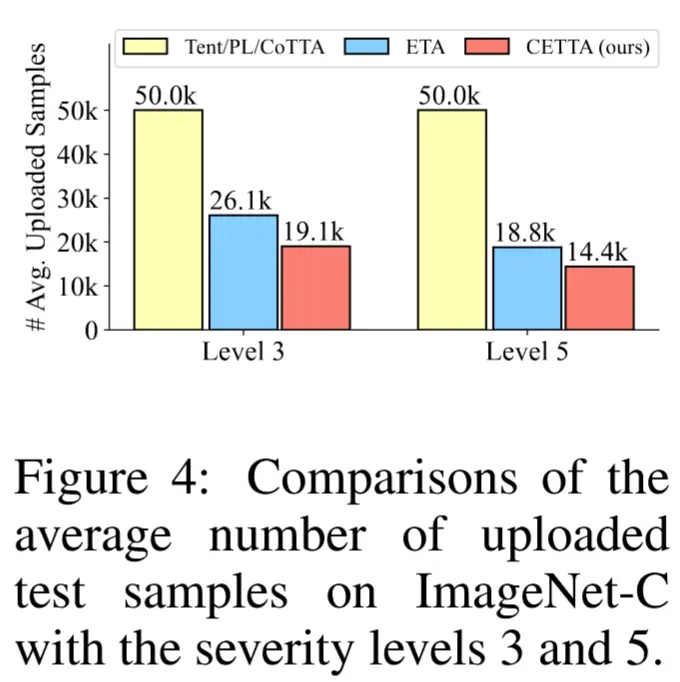
  • 比较CEMA与现有方法在15种损坏类型下的平均上传样本数量
    • 如图4所示
    • 结果：PL、Tent和CoTTA需要上传所有测试样本；ETA通过排除高预测熵的样本，减少了上传样本数量，但是仍然比CMEA多。
paper17-6.webp

3.2 在ImageNet-R上的性能对比

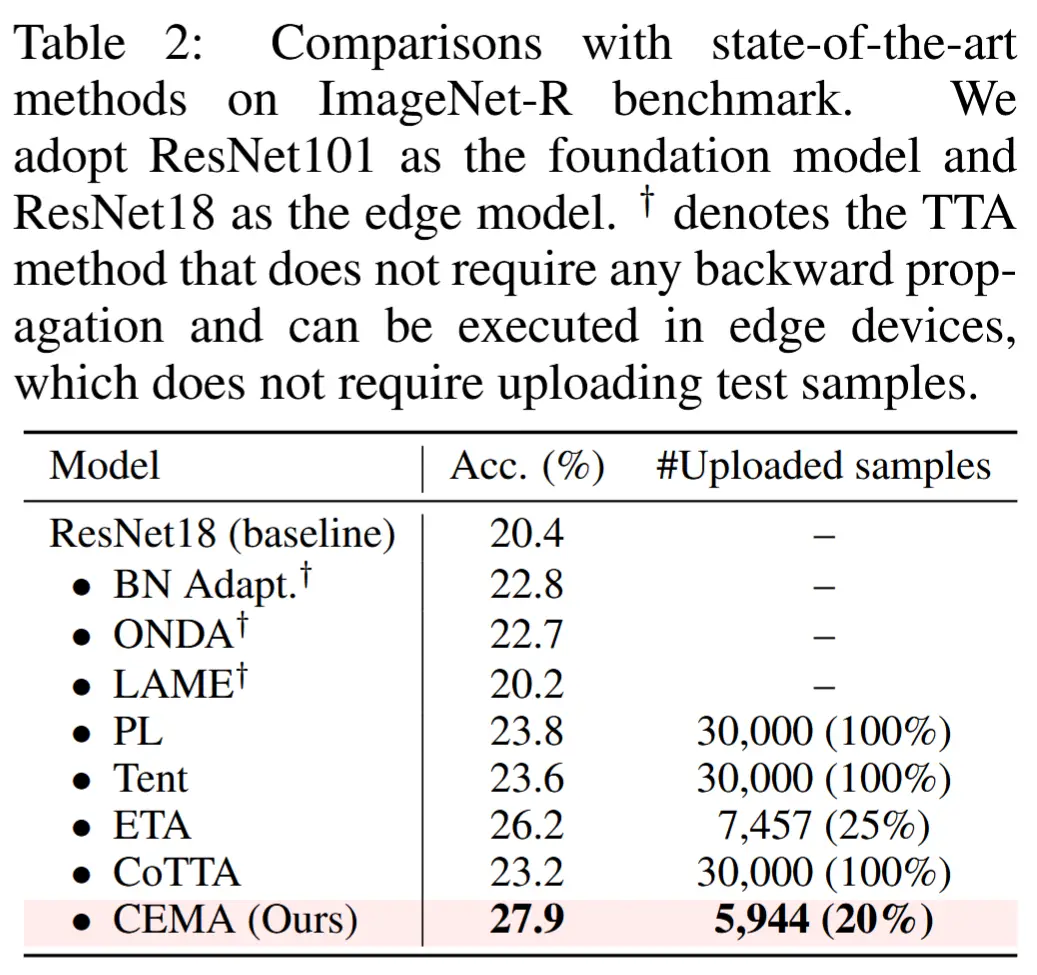
  • 与 ImageNet-R 基准测试中最先进的方法进行比较
    • 如表2所示
    • 结果：CEMA 在 ImageNet-R 上的准确率达到 27.9% ，优于其他方法；CEMA 仅需上传 5,944 个样本（20%）。
paper17-7.webp

4 结论

在本文中，作者设计了一种云边缘弹性模型自适应 (CEMA) 范式，通过利用云服务器和边缘设备来提高模型自适应性能。在自适应中， CEMA 不会在边缘设备中引入任何额外的计算成本。具体来说，我们设计了一种样本过滤策略，以从云中排除不必要的样本进行自适应。它减少了云和边缘之间的数据传输开销，从而提高了自适应效率。此外，作者采用强大的基础模型通过提出的基于重放的知识提炼来指导边缘模型进行自适应。在多个基准数据集上的大量实验结果证明了 CEMA 的有效性。

边缘智能 论文笔记 TTA